第19章 矩形、菱形与正方形试题(含答案)
文档属性
| 名称 | 第19章 矩形、菱形与正方形试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 678.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:47:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华东师大版八年级数学下册
第19章 矩形、菱形与正方形试题
姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.下列图形,既是轴对称图形又是中心对称图形的是( )
A.平行四边形 B.等腰三角形 C.正方形 D.菱形
2已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
A.AB=CD B.AC=BD
C.当AC⊥BD时,它是菱形 D.当∠ABC=90°时,它是矩形
3.如图,边长为6的正方形中,点E、F分别在边、上,连接、、,已知平分,,则的长为( )
A.2 B.3 C. D.
4如图,在平面直角坐标系中,点的坐标为,过点作轴于点,轴于点,点在上,将△CAD沿直线翻折,点恰好落在轴上的点处,则点的坐标为( )
A. B. C. D.
5.如图①,在矩形的边上有一点,连结,点从顶点出发,沿以1cm/s的速度匀速运动到点.图②是点运动时,△APE的面积随时间变化的函数图象,则的长为( )
A.2cm B.3cm C.4cm D.5cm
6.如图所示,正方形的面积为9,△ABE是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A.4.5 B.3 C.2.5 D.2
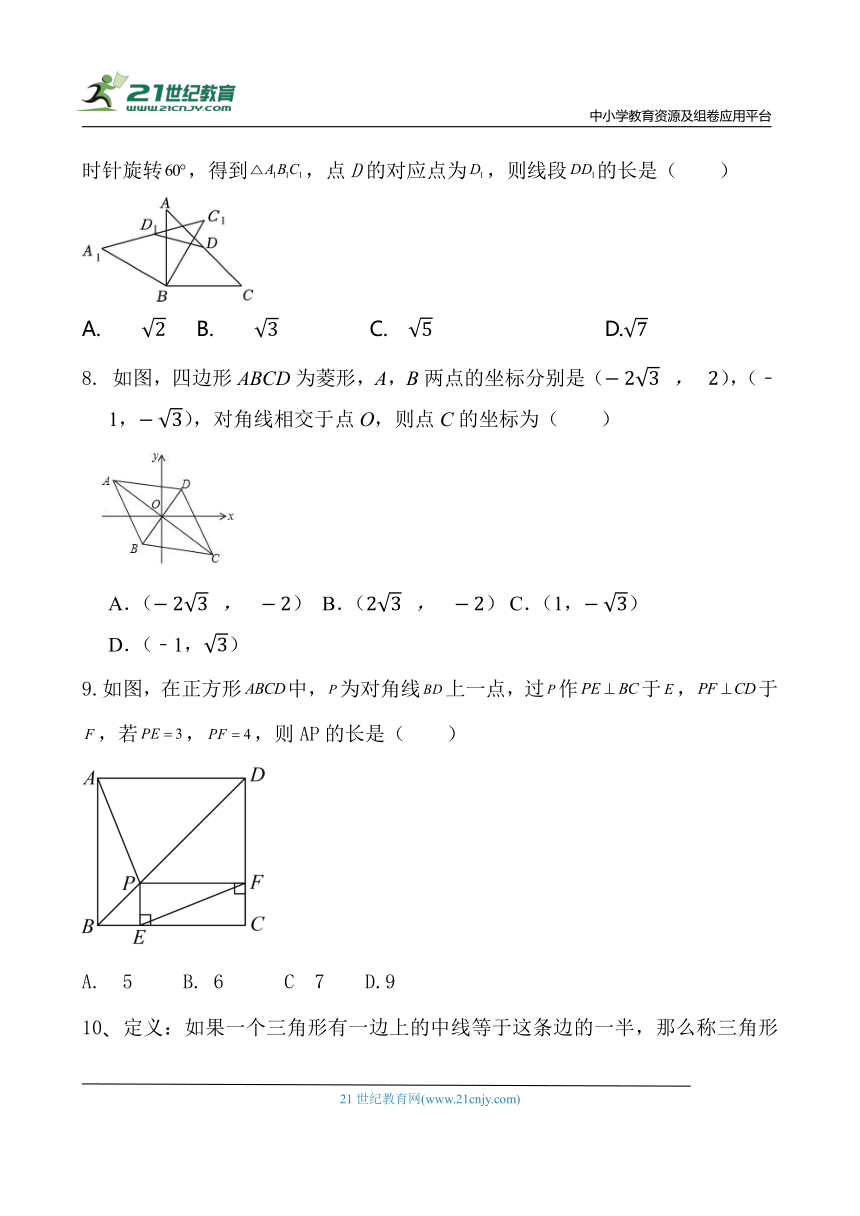
7. 如图,在中,,,点D是中点.将绕点B逆时针旋转,得到,点D的对应点为,则线段的长是( )
A. B. C. D.
8. 如图,四边形ABCD为菱形,A,B两点的坐标分别是(),(﹣1,),对角线相交于点O,则点C的坐标为( )
A.() B.() C.(1,)
D.(﹣1,)
9.如图,在正方形中,为对角线上一点,过作于,于,若,,则AP的长是( )
A. 5 B. 6 C 7 D.9
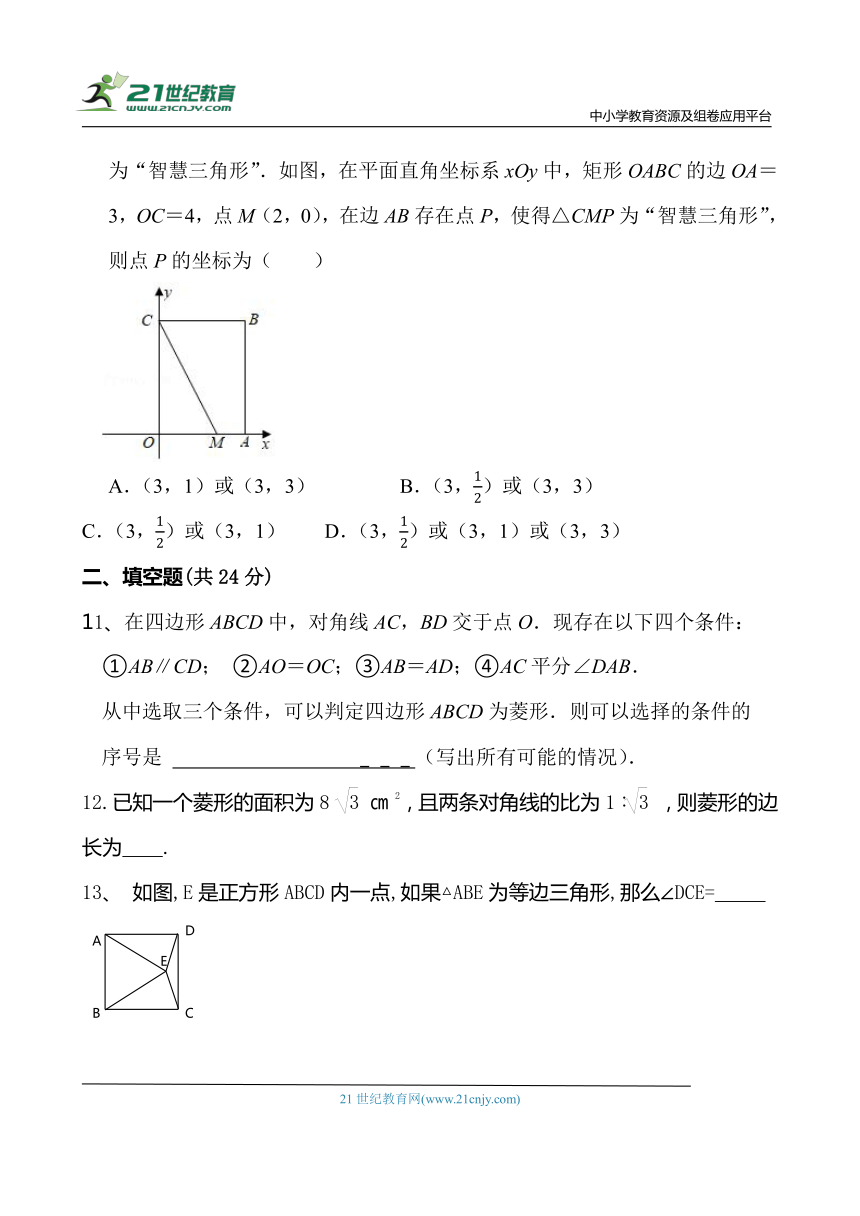
10、定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
二、填空题(共24分)
11、在四边形ABCD中,对角线AC,BD交于点O.现存在以下四个条件:
①AB∥CD; ②AO=OC;③AB=AD;④AC平分∠DAB.
从中选取三个条件,可以判定四边形ABCD为菱形.则可以选择的条件的
序号是 ___(写出所有可能的情况).
12.已知一个菱形的面积为8㎝2,且两条对角线的比为1∶,则菱形的边长为 .
13、 如图,E是正方形ABCD内一点,如果△ABE为等边三角形,那么∠DCE=
14、如图,菱形的边的垂直平分线交于点,交于点,连接.当时,
15. 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则平行四边形ABCD的最大内角的大小是 .
16、如图,在三角形ABC中,,,,将三角形ABC绕点按顺时针旋转一定角度得到三角形ADE,当点的对应点恰好落在边上时,则的长为 ______ .
17、如图,把一张矩形纸片沿对角线折叠,如果量得∠EDF=22°,则∠FDB的大小是
18. 我们把两条对角线所成两个角的大小之比是1:2的矩形叫做“和谐矩形”,如果一个“和谐矩形”的对角线长为10cm,则矩形的面积为 .
三、解答题(共66分)
19.(本题12分) 】如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE= °时,四边形BECD是菱形.
20.(本题14分)已知 ABCD,对角线AC,BD相交于点O(AC>BD),点E,F分别是OA,OC上的动点.
(1)如图①,若AE=CF,求证:四边形EBFD是平行四边形;
(2)如图②,若OE=OB,OF=OD,求证:四边形EBFD是矩形.
21.(本题13分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是线段AC上两动点,同时分别从A,C两点出发以1cm/s的速度向点C,A运动.
(1)求证:△ADE≌△CBF;
(2)若BD=8cm,AC=14cm,当运动时间t为多少秒时,四边形DEBF是矩形?
22.(本题13分)如图,在平行四边形ABCD中,CE平分∠BCD,交AB边于点E,EF∥BC,交CD于点F,点G是BC边的中点,连接GF,且∠1=∠2,CE与GF交于点M,过点M作MH⊥CD于点H.
(1)求证:四边形BCFE是菱形;
(2)若CH=1,求BC的长;
(3)求证:EM=FG+MH.
23.(本题14分)如图,在矩形中,以O为坐标原点,、分别在x轴、y轴上,点A的坐标为,点B的坐标为,点E是边上的一点,把矩形沿AE翻折后,点C恰好落在x轴上的点F处,且.
(1)求点E、F的坐标;
(2)求所在直线的函数关系式;
(3)在x轴上求一点P,使成为以为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.
参考答案
1.C 2.B 3.B 4.B 5.A 6.B 7.A .8.B 9. A 10.D
11.②③④; 12.4 cm ; 13. 15°; 14.30°; 15.150°;16. 1.6;
17. 34°;18. cm2
19.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)90°
解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,AB∥CD,
∴∠ADC=180°﹣∠A=130°,
∵四边形BECD是菱形,
∴BC⊥DE,
∴∠COD=90°,
∴∠ODC=90°﹣∠BCD=40°,
∴∠ADE=∠ADC﹣∠ODC=90°
20.证明:(1)∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF.
∴OA﹣AE=OC﹣CF,
即OE=OF,
∵OB=OD,
∴四边形EBFD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,OF=OD,
∴OE=OF=OB=OD,
∴四边形EBFD是平行四边形,BD=EF,
∴平行四边形EBFD是矩形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF
∵E,F是线段AC上两动点,同时分别从A,C两点出发以1cm/s的速度向点C,A运动,
∴AE=CF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∵AE=CF,
∴OE=OF
∴四边形DEBF为平行四边形,
∴当BD=EF时,四边形DEBF为矩形,
∴OE=ODBD,即AC﹣tBD或tACBD,
∴14﹣t8或t148,
解得:t=3(s)或t=11(s),
∴当运动时间t为3秒或11秒时,四边形DEBF是矩形.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠ECF,
∵EF∥BC,
∴四边形BCFE是平行四边形,
∵CE平分∠BCD,
∴∠BCE=∠ECF,
∴∠BCE=∠1,
∴BC=BE,
∴四边形BCFE是菱形;
(2)∵∠1=∠ECF,∠1=∠2,
∴∠ECF=∠2,
∴CM=FM,
∵MH⊥CD,
∴CF=2CH=2×1=2,
∵四边形BCFE是菱形;
∴BC=CF=2;
(3)连接BF交CE于点O,
∵G是BC中点,
∴CGCB,
∵CHCF,
∴CG=CH,
在△CGM和△CHM中,
,
∴△CGM≌△CHM(SAS),
∴∠CGM=∠CHM=90°,
即FG⊥BC,
∴CF=BF,
∵BC=CF,
∴BC=CF=BF,
∴△BCF是等边三角形,
∴∠BFC=60°,
∴∠2=∠BFG=30°,
∵BF⊥CE,
∴OM=MH,
∵OE=OC=FG,
∴EM=FG+MH.
23.(1)解:点的坐标为,点的坐标为,
,,
由折叠可知:,
则,
则点,
,
,
所以点;
(2)将点(0,8)、(6,0)的坐标代入一次函数表达式:并解得:
,,
故直线的表达式为:;
(3)①当点在轴负半轴时,
,则点;
当时,点;
②当点在轴正半轴时,
,故点;
综上,点的坐标为:或或.
21世纪教育网(www.21cnjy.com)
华东师大版八年级数学下册
第19章 矩形、菱形与正方形试题
姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.下列图形,既是轴对称图形又是中心对称图形的是( )
A.平行四边形 B.等腰三角形 C.正方形 D.菱形
2已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
A.AB=CD B.AC=BD
C.当AC⊥BD时,它是菱形 D.当∠ABC=90°时,它是矩形
3.如图,边长为6的正方形中,点E、F分别在边、上,连接、、,已知平分,,则的长为( )
A.2 B.3 C. D.
4如图,在平面直角坐标系中,点的坐标为,过点作轴于点,轴于点,点在上,将△CAD沿直线翻折,点恰好落在轴上的点处,则点的坐标为( )
A. B. C. D.
5.如图①,在矩形的边上有一点,连结,点从顶点出发,沿以1cm/s的速度匀速运动到点.图②是点运动时,△APE的面积随时间变化的函数图象,则的长为( )
A.2cm B.3cm C.4cm D.5cm
6.如图所示,正方形的面积为9,△ABE是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A.4.5 B.3 C.2.5 D.2
7. 如图,在中,,,点D是中点.将绕点B逆时针旋转,得到,点D的对应点为,则线段的长是( )
A. B. C. D.
8. 如图,四边形ABCD为菱形,A,B两点的坐标分别是(),(﹣1,),对角线相交于点O,则点C的坐标为( )
A.() B.() C.(1,)
D.(﹣1,)
9.如图,在正方形中,为对角线上一点,过作于,于,若,,则AP的长是( )
A. 5 B. 6 C 7 D.9
10、定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A.(3,1)或(3,3) B.(3,)或(3,3)
C.(3,)或(3,1) D.(3,)或(3,1)或(3,3)
二、填空题(共24分)
11、在四边形ABCD中,对角线AC,BD交于点O.现存在以下四个条件:
①AB∥CD; ②AO=OC;③AB=AD;④AC平分∠DAB.
从中选取三个条件,可以判定四边形ABCD为菱形.则可以选择的条件的
序号是 ___(写出所有可能的情况).
12.已知一个菱形的面积为8㎝2,且两条对角线的比为1∶,则菱形的边长为 .
13、 如图,E是正方形ABCD内一点,如果△ABE为等边三角形,那么∠DCE=
14、如图,菱形的边的垂直平分线交于点,交于点,连接.当时,
15. 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则平行四边形ABCD的最大内角的大小是 .
16、如图,在三角形ABC中,,,,将三角形ABC绕点按顺时针旋转一定角度得到三角形ADE,当点的对应点恰好落在边上时,则的长为 ______ .
17、如图,把一张矩形纸片沿对角线折叠,如果量得∠EDF=22°,则∠FDB的大小是
18. 我们把两条对角线所成两个角的大小之比是1:2的矩形叫做“和谐矩形”,如果一个“和谐矩形”的对角线长为10cm,则矩形的面积为 .
三、解答题(共66分)
19.(本题12分) 】如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE= °时,四边形BECD是菱形.
20.(本题14分)已知 ABCD,对角线AC,BD相交于点O(AC>BD),点E,F分别是OA,OC上的动点.
(1)如图①,若AE=CF,求证:四边形EBFD是平行四边形;
(2)如图②,若OE=OB,OF=OD,求证:四边形EBFD是矩形.
21.(本题13分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是线段AC上两动点,同时分别从A,C两点出发以1cm/s的速度向点C,A运动.
(1)求证:△ADE≌△CBF;
(2)若BD=8cm,AC=14cm,当运动时间t为多少秒时,四边形DEBF是矩形?
22.(本题13分)如图,在平行四边形ABCD中,CE平分∠BCD,交AB边于点E,EF∥BC,交CD于点F,点G是BC边的中点,连接GF,且∠1=∠2,CE与GF交于点M,过点M作MH⊥CD于点H.
(1)求证:四边形BCFE是菱形;
(2)若CH=1,求BC的长;
(3)求证:EM=FG+MH.
23.(本题14分)如图,在矩形中,以O为坐标原点,、分别在x轴、y轴上,点A的坐标为,点B的坐标为,点E是边上的一点,把矩形沿AE翻折后,点C恰好落在x轴上的点F处,且.
(1)求点E、F的坐标;
(2)求所在直线的函数关系式;
(3)在x轴上求一点P,使成为以为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.
参考答案
1.C 2.B 3.B 4.B 5.A 6.B 7.A .8.B 9. A 10.D
11.②③④; 12.4 cm ; 13. 15°; 14.30°; 15.150°;16. 1.6;
17. 34°;18. cm2
19.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)90°
解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,AB∥CD,
∴∠ADC=180°﹣∠A=130°,
∵四边形BECD是菱形,
∴BC⊥DE,
∴∠COD=90°,
∴∠ODC=90°﹣∠BCD=40°,
∴∠ADE=∠ADC﹣∠ODC=90°
20.证明:(1)∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF.
∴OA﹣AE=OC﹣CF,
即OE=OF,
∵OB=OD,
∴四边形EBFD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,OF=OD,
∴OE=OF=OB=OD,
∴四边形EBFD是平行四边形,BD=EF,
∴平行四边形EBFD是矩形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF
∵E,F是线段AC上两动点,同时分别从A,C两点出发以1cm/s的速度向点C,A运动,
∴AE=CF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∵AE=CF,
∴OE=OF
∴四边形DEBF为平行四边形,
∴当BD=EF时,四边形DEBF为矩形,
∴OE=ODBD,即AC﹣tBD或tACBD,
∴14﹣t8或t148,
解得:t=3(s)或t=11(s),
∴当运动时间t为3秒或11秒时,四边形DEBF是矩形.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠ECF,
∵EF∥BC,
∴四边形BCFE是平行四边形,
∵CE平分∠BCD,
∴∠BCE=∠ECF,
∴∠BCE=∠1,
∴BC=BE,
∴四边形BCFE是菱形;
(2)∵∠1=∠ECF,∠1=∠2,
∴∠ECF=∠2,
∴CM=FM,
∵MH⊥CD,
∴CF=2CH=2×1=2,
∵四边形BCFE是菱形;
∴BC=CF=2;
(3)连接BF交CE于点O,
∵G是BC中点,
∴CGCB,
∵CHCF,
∴CG=CH,
在△CGM和△CHM中,
,
∴△CGM≌△CHM(SAS),
∴∠CGM=∠CHM=90°,
即FG⊥BC,
∴CF=BF,
∵BC=CF,
∴BC=CF=BF,
∴△BCF是等边三角形,
∴∠BFC=60°,
∴∠2=∠BFG=30°,
∵BF⊥CE,
∴OM=MH,
∵OE=OC=FG,
∴EM=FG+MH.
23.(1)解:点的坐标为,点的坐标为,
,,
由折叠可知:,
则,
则点,
,
,
所以点;
(2)将点(0,8)、(6,0)的坐标代入一次函数表达式:并解得:
,,
故直线的表达式为:;
(3)①当点在轴负半轴时,
,则点;
当时,点;
②当点在轴正半轴时,
,故点;
综上,点的坐标为:或或.
21世纪教育网(www.21cnjy.com)
