10.1 相交线 - 第2课时 - 垂线 课件 (共30张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 10.1 相交线 - 第2课时 - 垂线 课件 (共30张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:30:24 | ||
图片预览








文档简介
(共30张PPT)
第 10章 相交线
10.1 相交线
第2课时 - 垂线
初中数学七年级下册(HK版)
学习目标
1.理解垂线、垂线段的概念,能用三角尺或量角器过一点画已知直线的垂线,掌握垂线的性质.
2.知道点到直线的距离的意义,能求解相关问题.
学习重难点
理解垂线、垂线段的概念,掌握垂线的性质.知道点到直线的距离的意义.
理解垂线、垂线段的概念,掌握垂线的性质.知道点到直线的距离的意义.
难点
重点
回顾复习
角的 名称 特 征 性质
对 顶 角
对顶角相等
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
创设情境
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
知识点 对顶角及其性质
新知引入
思考
将十字街口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么?
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫做垂足.
两条直线垂直的例子很多,你能再举出一些两条直线互相垂直的例子吗?
窗户的四边
围栏
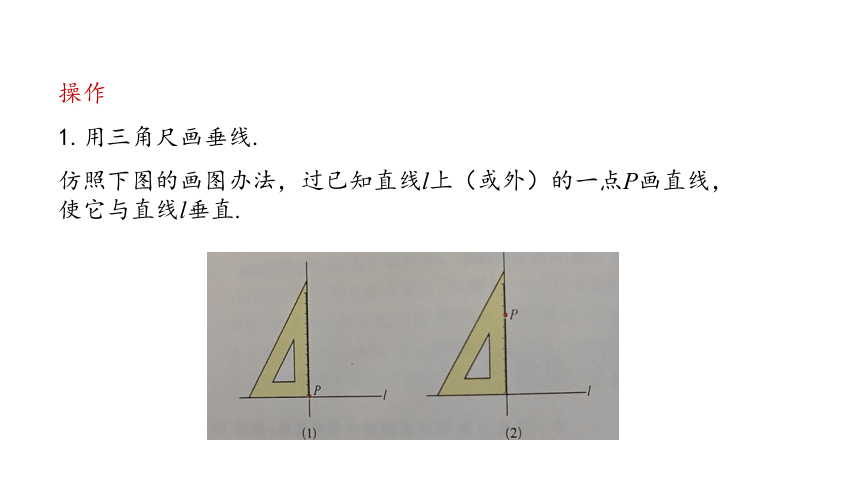
操作
1.用三角尺画垂线.
仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
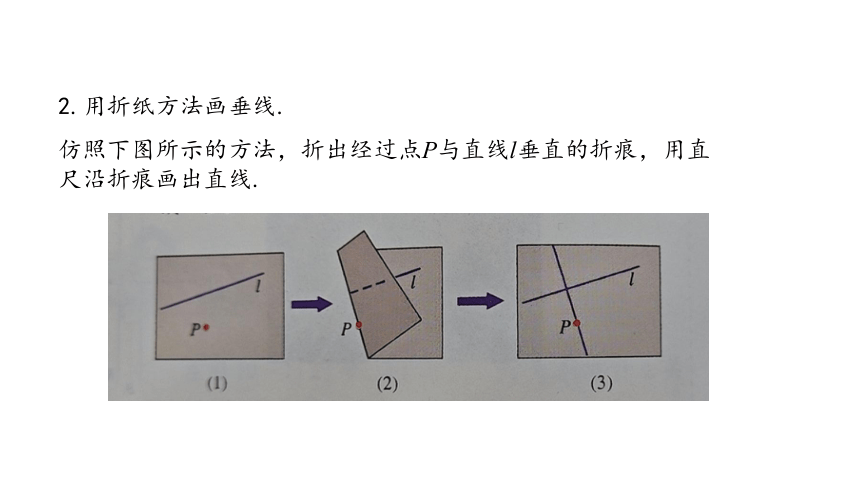
2.用折纸方法画垂线.
仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线.
1.落.
2.画.
如图,已知直线 l,作 l 的垂线.
l
O
A
这样画直线 l 的垂线可以画几条?
无数条.
通过上面的操作,你知道过一点画已知直线的垂线,能画几条吗?
l
A
B
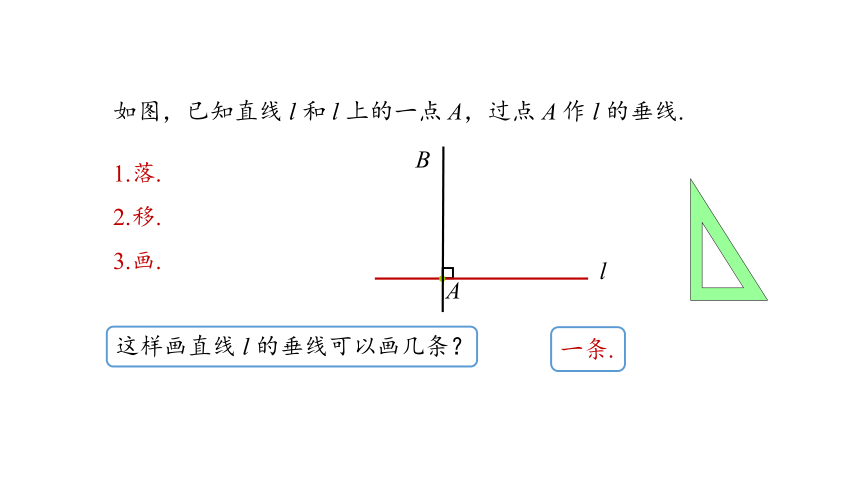
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
l
A
B
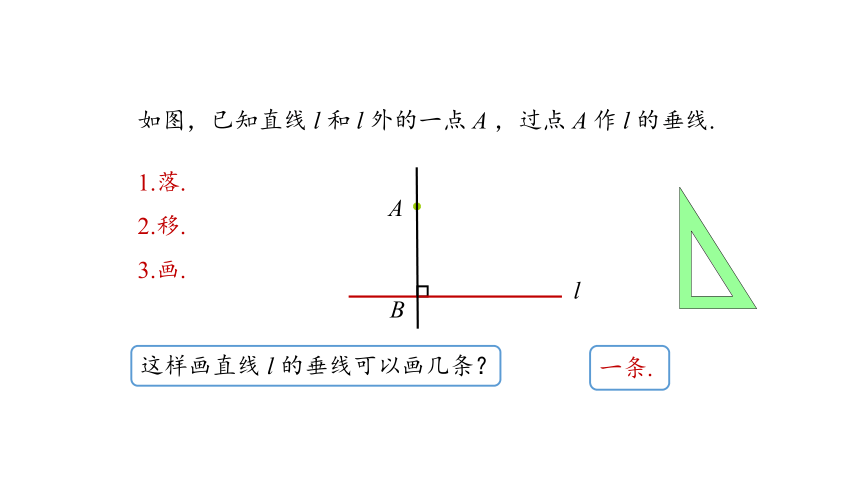
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂线,实际上是作线段所在的直线互相垂直,或作射线所在的直线的垂线,因为射线和线段都是直线的一部分.在垂线的画法中,有时需延长线段,垂足在延长线上,并记上直角符号“﹁”.
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
垂线的基本事实:过一点有且只有一条直线垂直于已知直线.
存在且唯一
注意:不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直.
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
观察
1.如图,点P在直线l外,在直线l上任意取一些点A,B,C,O,把这些点分别与点P连接,得到线段PA,PB,PC,PO,其中PO⊥l.观察这些线段,比较它们的长短,其中哪一条线段最短?
2.点P在直线l外,把一根细绳的一端用图钉固定在点P处,拉紧细绳,按如图所示步骤进行操作.
观察细绳上的标记点O(垂直拉紧时的垂足)位置的变化,你有什么发现?
垂线性质:在连接直线外一点与直线上各点的线段中,垂线段(连接直线外一点与垂足形成的线段)最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
总结归纳:
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
例题示范
例 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:垂线段最短
N
随堂练习
1.如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
2.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
5
3.如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
因为AB ⊥ l ,BC ⊥ l . 且交点都为 B .
所以A、B、C 三点在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直).
4.如图,AO⊥FD,OD 为∠BOC 的平分线,OE 为射线OB 的反向延长线,若∠AOB = 40°,求∠EOF、∠COE 的度数.
解:因为AO⊥OD且∠AOB=40°,
所以∠BOD=90°-40°=50°,所以∠EOF=50°.
又因为OD平分∠BOC,所以∠DOC=∠BOD=50°,
所以∠COE=180°-50°-50°=80°.
A
F
D
O
B
C
E
5.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
解:(1)如图,连接AD,BC 交于 H ,因为两点之间线段最短,所以 H 为蓄水池位置,它到四个村庄距离之和最小.
H
(2)如图,过 H 作 HG⊥EF ,垂足为 G .“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA =
2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm
B.小于 2 cm
C.大于 2cm
D.不大于 2 cm
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
B
3.如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
解:(1)因为 OM ⊥ AB ,所以∠1 + ∠AOC = 90°.又∠1 = ∠2,所以∠2 + ∠AOC = 90°,所以∠NOD = 180°-(∠2 + ∠AOC)= 180°- 90°= 90°.
(2)由已知条件∠BOC =4∠1,即 90°+∠1 = 4∠1,可得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,所以由对顶角相等可得∠BOD = 60°,所以∠MOD =90°+∠BOD = 150°.
归纳小结
垂线
垂线和垂线段
定义
性质
垂线段
定义
点到直线的距离
过一点有且只有一条直线垂直于已知直线
垂线段最短
第 10章 相交线
10.1 相交线
第2课时 - 垂线
初中数学七年级下册(HK版)
学习目标
1.理解垂线、垂线段的概念,能用三角尺或量角器过一点画已知直线的垂线,掌握垂线的性质.
2.知道点到直线的距离的意义,能求解相关问题.
学习重难点
理解垂线、垂线段的概念,掌握垂线的性质.知道点到直线的距离的意义.
理解垂线、垂线段的概念,掌握垂线的性质.知道点到直线的距离的意义.
难点
重点
回顾复习
角的 名称 特 征 性质
对 顶 角
对顶角相等
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
创设情境
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
知识点 对顶角及其性质
新知引入
思考
将十字街口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么?
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫做垂足.
两条直线垂直的例子很多,你能再举出一些两条直线互相垂直的例子吗?
窗户的四边
围栏
操作
1.用三角尺画垂线.
仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
2.用折纸方法画垂线.
仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线.
1.落.
2.画.
如图,已知直线 l,作 l 的垂线.
l
O
A
这样画直线 l 的垂线可以画几条?
无数条.
通过上面的操作,你知道过一点画已知直线的垂线,能画几条吗?
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条?
一条.
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂线,实际上是作线段所在的直线互相垂直,或作射线所在的直线的垂线,因为射线和线段都是直线的一部分.在垂线的画法中,有时需延长线段,垂足在延长线上,并记上直角符号“﹁”.
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
垂线的基本事实:过一点有且只有一条直线垂直于已知直线.
存在且唯一
注意:不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直.
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
观察
1.如图,点P在直线l外,在直线l上任意取一些点A,B,C,O,把这些点分别与点P连接,得到线段PA,PB,PC,PO,其中PO⊥l.观察这些线段,比较它们的长短,其中哪一条线段最短?
2.点P在直线l外,把一根细绳的一端用图钉固定在点P处,拉紧细绳,按如图所示步骤进行操作.
观察细绳上的标记点O(垂直拉紧时的垂足)位置的变化,你有什么发现?
垂线性质:在连接直线外一点与直线上各点的线段中,垂线段(连接直线外一点与垂足形成的线段)最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
总结归纳:
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
例题示范
例 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:垂线段最短
N
随堂练习
1.如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
2.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
5
3.如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
因为AB ⊥ l ,BC ⊥ l . 且交点都为 B .
所以A、B、C 三点在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直).
4.如图,AO⊥FD,OD 为∠BOC 的平分线,OE 为射线OB 的反向延长线,若∠AOB = 40°,求∠EOF、∠COE 的度数.
解:因为AO⊥OD且∠AOB=40°,
所以∠BOD=90°-40°=50°,所以∠EOF=50°.
又因为OD平分∠BOC,所以∠DOC=∠BOD=50°,
所以∠COE=180°-50°-50°=80°.
A
F
D
O
B
C
E
5.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
解:(1)如图,连接AD,BC 交于 H ,因为两点之间线段最短,所以 H 为蓄水池位置,它到四个村庄距离之和最小.
H
(2)如图,过 H 作 HG⊥EF ,垂足为 G .“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA =
2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm
B.小于 2 cm
C.大于 2cm
D.不大于 2 cm
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
B
3.如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
解:(1)因为 OM ⊥ AB ,所以∠1 + ∠AOC = 90°.又∠1 = ∠2,所以∠2 + ∠AOC = 90°,所以∠NOD = 180°-(∠2 + ∠AOC)= 180°- 90°= 90°.
(2)由已知条件∠BOC =4∠1,即 90°+∠1 = 4∠1,可得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,所以由对顶角相等可得∠BOD = 60°,所以∠MOD =90°+∠BOD = 150°.
归纳小结
垂线
垂线和垂线段
定义
性质
垂线段
定义
点到直线的距离
过一点有且只有一条直线垂直于已知直线
垂线段最短
