10.2 平行线的判定 - 第2课时 - 同位角、内错角、同旁内角 课件 (共25张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 10.2 平行线的判定 - 第2课时 - 同位角、内错角、同旁内角 课件 (共25张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 572.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
第 10章 相交线
10.2 平行线的判定
第2课时 - 同位角、内错角、同旁内角
初中数学七年级下册(HK版)
学习目标
1.理解什么是同位角、内错角、同旁内角,能正确识别图形中的同位角、内错角和同旁内角.
2.能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
学习重难点
理解什么是同位角、内错角、同旁内角,能正确识别图形中的同位角、内错角和同旁内角.
能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
难点
重点
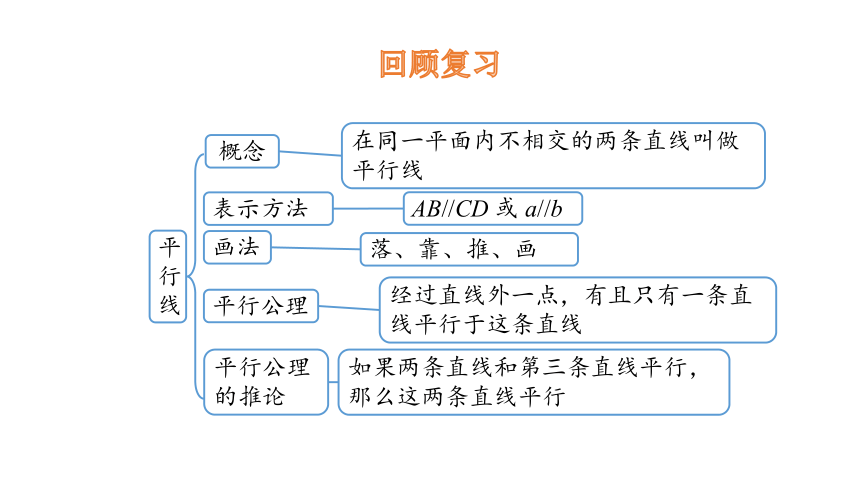
回顾复习
表示方法
平行
线
如果两条直线和第三条直线平行,那么这两条直线平行
画法
平行公理
平行公理的推论
概念
落、靠、推、画
经过直线外一点,有且只有一条直线平行于这条直线
在同一平面内不相交的两条直线叫做平行线
AB//CD 或 a//b
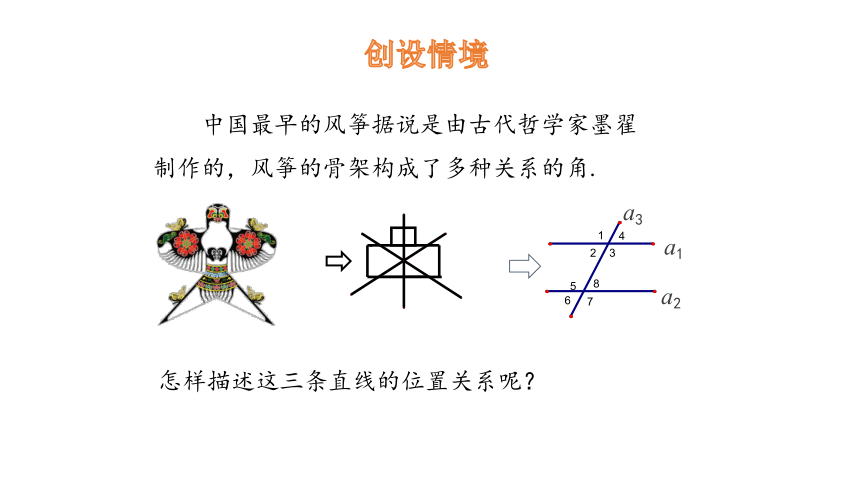
创设情境
中国最早的风筝据说是由古代哲学家墨翟制作的,风筝的骨架构成了多种关系的角.
怎样描述这三条直线的位置关系呢?
a1
a2
a3
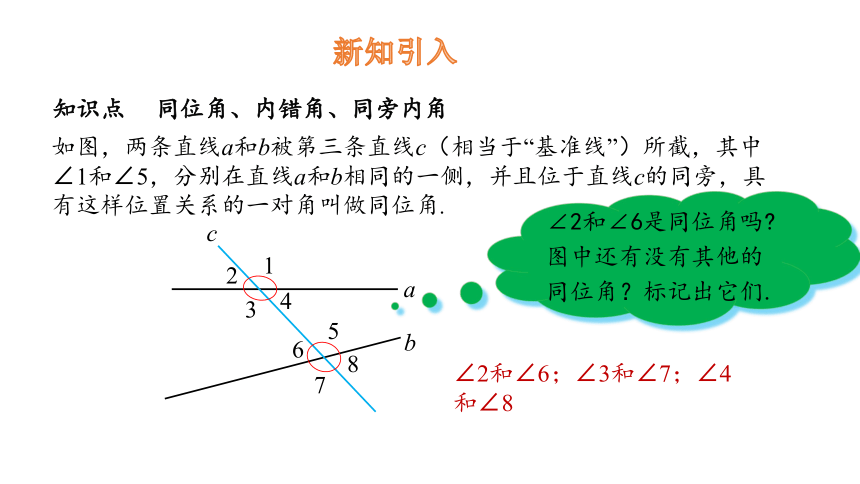
知识点 同位角、内错角、同旁内角
新知引入
如图,两条直线a和b被第三条直线c(相当于“基准线”)所截,其中∠1和∠5,分别在直线a和b相同的一侧,并且位于直线c的同旁,具有这样位置关系的一对角叫做同位角.
∠2和∠6是同位角吗 图中还有没有其他的同位角?标记出它们.
1
3
2
4
5
7
6
8
a
b
c
∠2和∠6;∠3和∠7;∠4和∠8
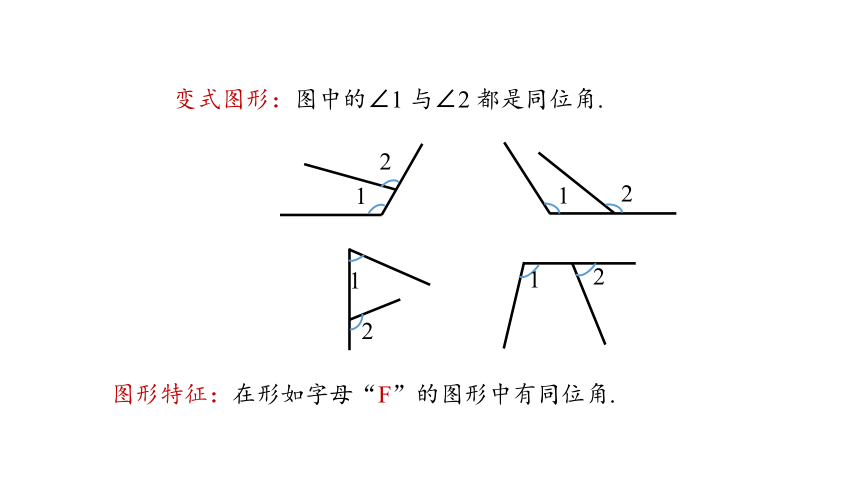
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
1
2
1
2
1
2
2
特别提醒:
1. 同位角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.同位角的顶点不是公共的 .
3.“同”表示“相同”,“位”表示“位置”.“同位角”可理解为“相同位置的两个角”,即如果一个角在左上方,那么另一个角也应在左上方.以此类推,两个同位角的位置关系具有 “同上、同左”“同上、同右” “同下、同左”“同下、同右的特征.
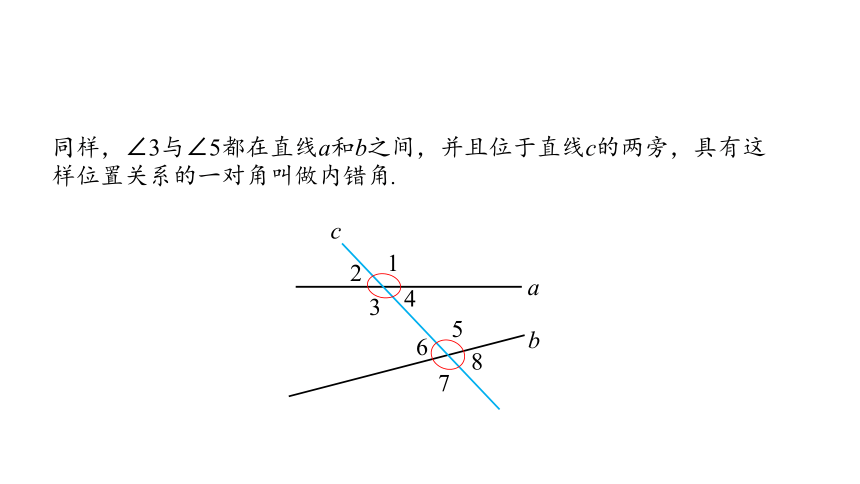
同样,∠3与∠5都在直线a和b之间,并且位于直线c的两旁,具有这样位置关系的一对角叫做内错角.
1
3
2
4
5
7
6
8
a
b
c
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
特别提醒:
1.内错角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.内错角的顶点不是公共的 .
3.“内”可理解为夹在两直线之间,“错”可理解为交错,即位于第三条直线的两侧 . 内错角的位置关系具有“同内、异侧 ”的特征.
∠4与∠5都在直线a和b之间,并且位于直线c的两旁,具有这样位置关系的一对角叫做同旁内角.
1
3
2
4
5
7
6
8
a
b
c
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
特别提醒:
1.同旁内角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.同旁内角的顶点不是公共的 .
3.“同旁”即在第三条直线的同一旁,“内”表示夹在两直线之间.同旁内角的位置关系具有“同内、同侧”的特征.
角的名称 位置特征 基本图形 结构特征 相同点 共同特征
同位角
同旁内角
内错角
F
Z
U
1
2
1
2
1
2
都在截线同侧
都没有
公共顶点
都在被截线之间
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
同位角、内错角、同旁内角的特征
注意:(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
判断三线八角的方法
1.把两个角在图中描画出来;
2.找到两个角的公共直线;
3.观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
三线八角手势记忆法
同位角
内错角
同旁内角
例 分别指出下列图中的同位角、内错角、同旁内角.
a
b
c
1
2
3
4
(2)
1
2
3
4
5
6
7
8
(1)
解:图(1)中,同位角有∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;内错角有∠4与∠5,∠3与∠6;同旁内角有∠3与∠5,∠4与∠6.
图(2)中,同位角有∠1与∠3,∠2与∠4,同旁内角有∠2与∠3;无内错角.
例题示范
随堂练习
1.如图,射线 AB,AC 被射线 DE 所截,图中的∠1 与∠2 是( )
A.内错角
B.对顶角
C.同位角
D.同旁内角
A
A
D
B
C
E
2
1
2.如图,给出下列四个结论:
①∠2 与∠6 是内错角;②∠3 与∠4 是内错角;
③∠5 与∠6 是同旁内角;④∠1 与∠4 是同旁内角.
其中正确的是( )
A.①② B.②③④
C.①②④ D.①②③④
C
3.如图:
①∠DAE 的同位角是______,它们是直线______
和直线______被直线______所截形成的.
②∠CAD 的内错角是______,它们是直线______
和直线______被直线______所截形成的.
③∠B 的同旁内角有______________________.
∠B
AD
BC
AB
∠C
AD
BC
AC
∠DAB,∠CAB,∠C
1.如图所示,下列说法中,错误的是( )
A.∠A 与∠EDC 是同位角
B.∠A 与∠C 是同旁内角
C.∠A 与∠ADC 是同旁内角
D.∠A 与∠ABF 是内错角
B
拓展提升
A
B
F
C
E
D
2.如图,已知∠1和∠2是内错角,则下列表述正确的是( )
A.∠1和∠2是由直线AD、AC被CE所截形成的
B.∠1和∠2是由直线AD、AC被BD所截形成的
C.∠1和∠2是由直线DA、DB被CE所截形成的
D.∠1和∠2是由直线DA、DB被AC所截形成的
B
3.如图,∠1 和∠2,∠3 和∠4 各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?
(1) (2)
解:(1)∠1 和∠2 是直线 AB、CD 被直线BD 所截形成的,是内错角;∠3 和∠4 是直线 AD、BC 被直线 BD 所截形成的,是内错角.
(2)∠1 和∠2 是直线 AB、CD 被直线BC所截形成的,是同旁内角;∠3 和∠4 是直线 AD、BC 被直线 AE 所截形成的,是同位角.
“F”型
“Z”型
“U”型
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角
内错角
同旁内角
归纳小结
2.在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
第 10章 相交线
10.2 平行线的判定
第2课时 - 同位角、内错角、同旁内角
初中数学七年级下册(HK版)
学习目标
1.理解什么是同位角、内错角、同旁内角,能正确识别图形中的同位角、内错角和同旁内角.
2.能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
学习重难点
理解什么是同位角、内错角、同旁内角,能正确识别图形中的同位角、内错角和同旁内角.
能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
难点
重点
回顾复习
表示方法
平行
线
如果两条直线和第三条直线平行,那么这两条直线平行
画法
平行公理
平行公理的推论
概念
落、靠、推、画
经过直线外一点,有且只有一条直线平行于这条直线
在同一平面内不相交的两条直线叫做平行线
AB//CD 或 a//b
创设情境
中国最早的风筝据说是由古代哲学家墨翟制作的,风筝的骨架构成了多种关系的角.
怎样描述这三条直线的位置关系呢?
a1
a2
a3
知识点 同位角、内错角、同旁内角
新知引入
如图,两条直线a和b被第三条直线c(相当于“基准线”)所截,其中∠1和∠5,分别在直线a和b相同的一侧,并且位于直线c的同旁,具有这样位置关系的一对角叫做同位角.
∠2和∠6是同位角吗 图中还有没有其他的同位角?标记出它们.
1
3
2
4
5
7
6
8
a
b
c
∠2和∠6;∠3和∠7;∠4和∠8
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
1
2
1
2
1
2
2
特别提醒:
1. 同位角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.同位角的顶点不是公共的 .
3.“同”表示“相同”,“位”表示“位置”.“同位角”可理解为“相同位置的两个角”,即如果一个角在左上方,那么另一个角也应在左上方.以此类推,两个同位角的位置关系具有 “同上、同左”“同上、同右” “同下、同左”“同下、同右的特征.
同样,∠3与∠5都在直线a和b之间,并且位于直线c的两旁,具有这样位置关系的一对角叫做内错角.
1
3
2
4
5
7
6
8
a
b
c
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
特别提醒:
1.内错角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.内错角的顶点不是公共的 .
3.“内”可理解为夹在两直线之间,“错”可理解为交错,即位于第三条直线的两侧 . 内错角的位置关系具有“同内、异侧 ”的特征.
∠4与∠5都在直线a和b之间,并且位于直线c的两旁,具有这样位置关系的一对角叫做同旁内角.
1
3
2
4
5
7
6
8
a
b
c
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
特别提醒:
1.同旁内角是成对出现的,并且是由三条直线组成的,即一对边共线,另一对边不共线 .
2.同旁内角的顶点不是公共的 .
3.“同旁”即在第三条直线的同一旁,“内”表示夹在两直线之间.同旁内角的位置关系具有“同内、同侧”的特征.
角的名称 位置特征 基本图形 结构特征 相同点 共同特征
同位角
同旁内角
内错角
F
Z
U
1
2
1
2
1
2
都在截线同侧
都没有
公共顶点
都在被截线之间
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
同位角、内错角、同旁内角的特征
注意:(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
判断三线八角的方法
1.把两个角在图中描画出来;
2.找到两个角的公共直线;
3.观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
三线八角手势记忆法
同位角
内错角
同旁内角
例 分别指出下列图中的同位角、内错角、同旁内角.
a
b
c
1
2
3
4
(2)
1
2
3
4
5
6
7
8
(1)
解:图(1)中,同位角有∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;内错角有∠4与∠5,∠3与∠6;同旁内角有∠3与∠5,∠4与∠6.
图(2)中,同位角有∠1与∠3,∠2与∠4,同旁内角有∠2与∠3;无内错角.
例题示范
随堂练习
1.如图,射线 AB,AC 被射线 DE 所截,图中的∠1 与∠2 是( )
A.内错角
B.对顶角
C.同位角
D.同旁内角
A
A
D
B
C
E
2
1
2.如图,给出下列四个结论:
①∠2 与∠6 是内错角;②∠3 与∠4 是内错角;
③∠5 与∠6 是同旁内角;④∠1 与∠4 是同旁内角.
其中正确的是( )
A.①② B.②③④
C.①②④ D.①②③④
C
3.如图:
①∠DAE 的同位角是______,它们是直线______
和直线______被直线______所截形成的.
②∠CAD 的内错角是______,它们是直线______
和直线______被直线______所截形成的.
③∠B 的同旁内角有______________________.
∠B
AD
BC
AB
∠C
AD
BC
AC
∠DAB,∠CAB,∠C
1.如图所示,下列说法中,错误的是( )
A.∠A 与∠EDC 是同位角
B.∠A 与∠C 是同旁内角
C.∠A 与∠ADC 是同旁内角
D.∠A 与∠ABF 是内错角
B
拓展提升
A
B
F
C
E
D
2.如图,已知∠1和∠2是内错角,则下列表述正确的是( )
A.∠1和∠2是由直线AD、AC被CE所截形成的
B.∠1和∠2是由直线AD、AC被BD所截形成的
C.∠1和∠2是由直线DA、DB被CE所截形成的
D.∠1和∠2是由直线DA、DB被AC所截形成的
B
3.如图,∠1 和∠2,∠3 和∠4 各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?
(1) (2)
解:(1)∠1 和∠2 是直线 AB、CD 被直线BD 所截形成的,是内错角;∠3 和∠4 是直线 AD、BC 被直线 BD 所截形成的,是内错角.
(2)∠1 和∠2 是直线 AB、CD 被直线BC所截形成的,是同旁内角;∠3 和∠4 是直线 AD、BC 被直线 AE 所截形成的,是同位角.
“F”型
“Z”型
“U”型
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角
内错角
同旁内角
归纳小结
2.在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
