10.3 平行线的性质 - 第2课时 - 平行线的性质与判定 课件 (共21张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 10.3 平行线的性质 - 第2课时 - 平行线的性质与判定 课件 (共21张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 193.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:58:36 | ||
图片预览






文档简介
(共21张PPT)
第 10章 相交线
10.3 平行线的性质
第2课时 - 平行线的性质与判定
初中数学七年级下册(HK版)
学习目标
1.进一步熟悉平行线的判定方法和性质.
2.能用平行线的性质和判定进行简单的推理和计算.
学习重难点
进一步熟悉平行线的判定方法和性质.
能用平行线的性质和判定进行简单的推理和计算.
难点
重点
回顾复习
判定两直线平行的方法有哪些?
定义法.
平行公理的推论.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质有哪些?
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
创设情境
前面我们学行线的判定方法和平行线的性质,实际上,在实际应用中,两者是相互结合使用的,下面我们就来看看应用平行线的判定和性质能解决哪些问题吧!
新知引入
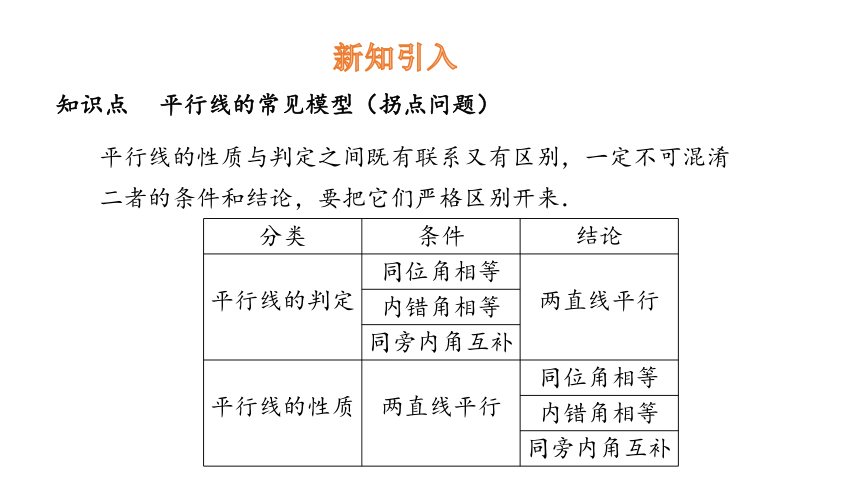
知识点 平行线的常见模型(拐点问题)
平行线的性质与判定之间既有联系又有区别,一定不可混淆二者的条件和结论,要把它们严格区别开来.
分类 条件 结论
平行线的判定 同位角相等
两直线平行
内错角相等
同旁内角互补
平行线的性质 两直线平行 同位角相等
内错角相等
同旁内角互补
A
B
C
D
E
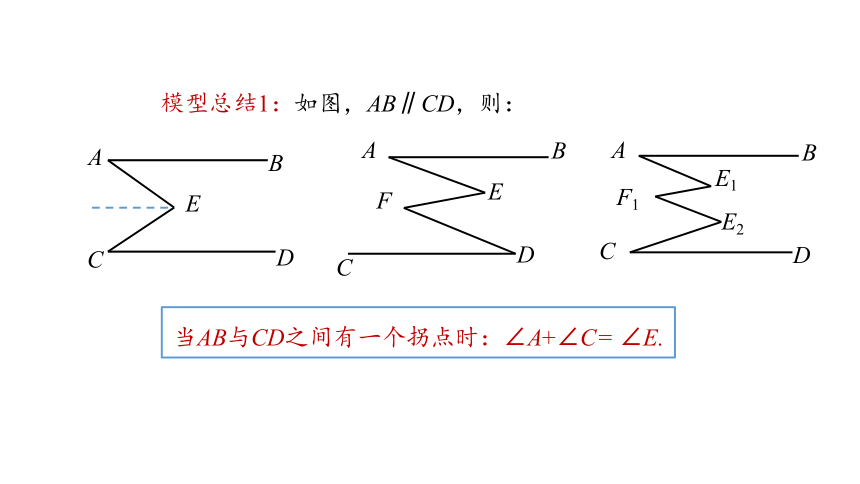
当AB与CD之间有一个拐点时:∠A+∠C= ∠E.
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
模型总结1:如图,AB∥CD,则:
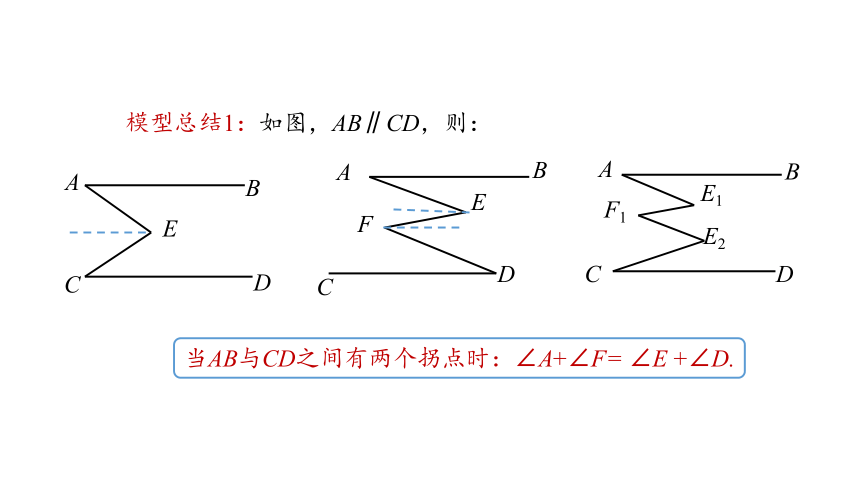
当AB与CD之间有两个拐点时:∠A+∠F= ∠E +∠D.
模型总结1:如图,AB∥CD,则:
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当AB与CD之间有三个拐点时:∠A+∠F1 +∠C = ∠E1 +∠E2.
模型总结1:如图,AB∥CD,则:
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
思考:如下图,你能找到∠A,∠F1 ,∠F2 ,… , ∠Fn-1与∠E1 ,E2 ,…,∠Em-1,∠D之间的关系吗?
∠A+∠F1 + ∠F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+ ∠Em-1+ ∠D
例题示范
例 如图,AB∥CD,猜想∠A、∠P 与∠PCD 之间的关系,并说明理由.
解:如图,过点P作PE ∥ AB.
因为AB∥CD,所以 PE ∥ AB ∥CD.
所以∠EPC=∠PCD,∠APE =∠A.
所以∠APE+∠APC=∠EPC= ∠PCD,
所以∠A+∠APC = ∠PCD.
A
B
C
D
P
E
模型总结2:如图,AB∥CD,则:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°.
A
B
C
D
E1
E2
E3
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
C
A
B
D
E
A
C
D
B
E2
E1
A
B
C
D
E1
E2
E3
模型总结2:如图,AB∥CD,则:
当有三个拐点时:∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
C
A
B
D
E
A
C
D
B
E2
E1
A
B
C
D
E1
E2
E3
模型总结2:如图,AB∥CD,则:
…
A
B
C
D
E1
E2
En
当有 n 个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C =(n+1)×180°.
思考:若有 n 个拐点,你能找到规律吗?
例题示范
例 如图,AB//CD,试说明∠B+∠D +∠DEB=360°.
解:过点 E 作 EF//AB.
所以∠B+∠BEF=180°.
因为AB//CD,∴EF//CD.
所以∠D +∠DEF=180°,
所以∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF =360°,
即∠B+∠D+∠DEB=360°.
F
C
A
B
D
E
随堂练习
1.把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
A. 45°
B. 60°
C. 75°
D. 82.5°
C
A
B
C
D
E
F
导引:过点 E 作 EF//AB.
2.如图,若 AB//CD,你能确定∠B、∠D 与∠BED 之间的关系吗?说说你的看法.
B
D
C
E
A
F
解:如图,过点 E 作 EF//AB.
所以∠B=∠BEF.
因为AB//CD,所以EF//CD.
所以∠D =∠DEF.
所以∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
拓展提升
∠P+∠A+∠C=360°
∠P=∠A+∠C
1.如图,AB//CD,分别探究下面四个图中∠P 与∠A,∠C之间的关系.
E
E
解:∠APC+∠A=∠C.理由如下:
过点 P 作 PE//AB,则∠EPA+∠A=180°.
因为∠EPA=∠APC+∠1,
所以∠APC+∠1+∠A=180°,
所以 ∠APC+∠A=180°-∠1.
因为 AB//CD,∴ PE//CD,
所以 ∠1+∠C=180°,所以 ∠C= 180°-∠1.
所以∠APC+∠A=∠C.
E
1
解:∠A=∠APC+∠C.理由如下:
过点 P 作 PE//AB,则∠1+∠A=180°.
因为 AB//CD,所以 PE//CD,
所以∠EPC+∠C=180°,即∠1+∠APC+∠C=180°,
所以180°-∠A+∠APC+∠C=180°.
所以∠A=∠APC+ ∠C.
E
1
(4)
归纳小结
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
性质
角的关系
线的关系
判定
第 10章 相交线
10.3 平行线的性质
第2课时 - 平行线的性质与判定
初中数学七年级下册(HK版)
学习目标
1.进一步熟悉平行线的判定方法和性质.
2.能用平行线的性质和判定进行简单的推理和计算.
学习重难点
进一步熟悉平行线的判定方法和性质.
能用平行线的性质和判定进行简单的推理和计算.
难点
重点
回顾复习
判定两直线平行的方法有哪些?
定义法.
平行公理的推论.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质有哪些?
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
创设情境
前面我们学行线的判定方法和平行线的性质,实际上,在实际应用中,两者是相互结合使用的,下面我们就来看看应用平行线的判定和性质能解决哪些问题吧!
新知引入
知识点 平行线的常见模型(拐点问题)
平行线的性质与判定之间既有联系又有区别,一定不可混淆二者的条件和结论,要把它们严格区别开来.
分类 条件 结论
平行线的判定 同位角相等
两直线平行
内错角相等
同旁内角互补
平行线的性质 两直线平行 同位角相等
内错角相等
同旁内角互补
A
B
C
D
E
当AB与CD之间有一个拐点时:∠A+∠C= ∠E.
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
模型总结1:如图,AB∥CD,则:
当AB与CD之间有两个拐点时:∠A+∠F= ∠E +∠D.
模型总结1:如图,AB∥CD,则:
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当AB与CD之间有三个拐点时:∠A+∠F1 +∠C = ∠E1 +∠E2.
模型总结1:如图,AB∥CD,则:
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
思考:如下图,你能找到∠A,∠F1 ,∠F2 ,… , ∠Fn-1与∠E1 ,E2 ,…,∠Em-1,∠D之间的关系吗?
∠A+∠F1 + ∠F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+ ∠Em-1+ ∠D
例题示范
例 如图,AB∥CD,猜想∠A、∠P 与∠PCD 之间的关系,并说明理由.
解:如图,过点P作PE ∥ AB.
因为AB∥CD,所以 PE ∥ AB ∥CD.
所以∠EPC=∠PCD,∠APE =∠A.
所以∠APE+∠APC=∠EPC= ∠PCD,
所以∠A+∠APC = ∠PCD.
A
B
C
D
P
E
模型总结2:如图,AB∥CD,则:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°.
A
B
C
D
E1
E2
E3
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
C
A
B
D
E
A
C
D
B
E2
E1
A
B
C
D
E1
E2
E3
模型总结2:如图,AB∥CD,则:
当有三个拐点时:∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
C
A
B
D
E
A
C
D
B
E2
E1
A
B
C
D
E1
E2
E3
模型总结2:如图,AB∥CD,则:
…
A
B
C
D
E1
E2
En
当有 n 个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C =(n+1)×180°.
思考:若有 n 个拐点,你能找到规律吗?
例题示范
例 如图,AB//CD,试说明∠B+∠D +∠DEB=360°.
解:过点 E 作 EF//AB.
所以∠B+∠BEF=180°.
因为AB//CD,∴EF//CD.
所以∠D +∠DEF=180°,
所以∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF =360°,
即∠B+∠D+∠DEB=360°.
F
C
A
B
D
E
随堂练习
1.把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
A. 45°
B. 60°
C. 75°
D. 82.5°
C
A
B
C
D
E
F
导引:过点 E 作 EF//AB.
2.如图,若 AB//CD,你能确定∠B、∠D 与∠BED 之间的关系吗?说说你的看法.
B
D
C
E
A
F
解:如图,过点 E 作 EF//AB.
所以∠B=∠BEF.
因为AB//CD,所以EF//CD.
所以∠D =∠DEF.
所以∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
拓展提升
∠P+∠A+∠C=360°
∠P=∠A+∠C
1.如图,AB//CD,分别探究下面四个图中∠P 与∠A,∠C之间的关系.
E
E
解:∠APC+∠A=∠C.理由如下:
过点 P 作 PE//AB,则∠EPA+∠A=180°.
因为∠EPA=∠APC+∠1,
所以∠APC+∠1+∠A=180°,
所以 ∠APC+∠A=180°-∠1.
因为 AB//CD,∴ PE//CD,
所以 ∠1+∠C=180°,所以 ∠C= 180°-∠1.
所以∠APC+∠A=∠C.
E
1
解:∠A=∠APC+∠C.理由如下:
过点 P 作 PE//AB,则∠1+∠A=180°.
因为 AB//CD,所以 PE//CD,
所以∠EPC+∠C=180°,即∠1+∠APC+∠C=180°,
所以180°-∠A+∠APC+∠C=180°.
所以∠A=∠APC+ ∠C.
E
1
(4)
归纳小结
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
性质
角的关系
线的关系
判定
