6.1 平方根、立方根 - 1.平方根 课件 (共25张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 6.1 平方根、立方根 - 1.平方根 课件 (共25张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第 6章 实数
6.1 平方根、立方根
1.平方根
初中数学七年级下册(HK版)
学习目标
1.了解平方根的概念,会表示一个数的平方根.
2.了解算术平方根的概念,会用根号表示一个正数的算术平方根.
3.了解平方和开方互为逆运算,会用平方运算求某些非负数的平方根.
4.会求一个正数的算术平方根,并解决实际问题.
学习重难点
1.了解平方根的概念,会表示一个数的平方根.
2.了解算术平方根的概念,会用根号表示一个正数的算术平方根.
1.了解平方和开方互为逆运算,会用平方运算求某些非负数的平方根.
2.会求一个正数的算术平方根,并解决实际问题.
难点
重点
创设情境
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1 m ,如图,问这种地砖一块的边长是多少?
知识点 平方根
新知引入
设一块正方形地砖的边长为x m,根据题意,有
x =
这是已知一个数的平方,求这个数的问题.
平方根的概念:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做二次方根.
例如,由于10 =100,(-10) =100,,所以100的平方根是+10和-10(可以合写为±10).
交流
1.16的平方根是什么? ±4
2.0的平方根是什么? 0
3.-9有没有平方根? 没有
一个正数a的平方根有两个,它们互为相反数.
我们用表示a的正的平方根,读作“根号a”,其中a叫做被开方数,这个根也叫做a的算术平方根,另一个负的平方根记为-.
0的平方根是0,0的算术平方根也是0,即=0.
负数没有平方根.
总结
中的a是一个非负数,a的算术平方根( )也是一个非负数,这也是算术平方根的性质——双重非负性.
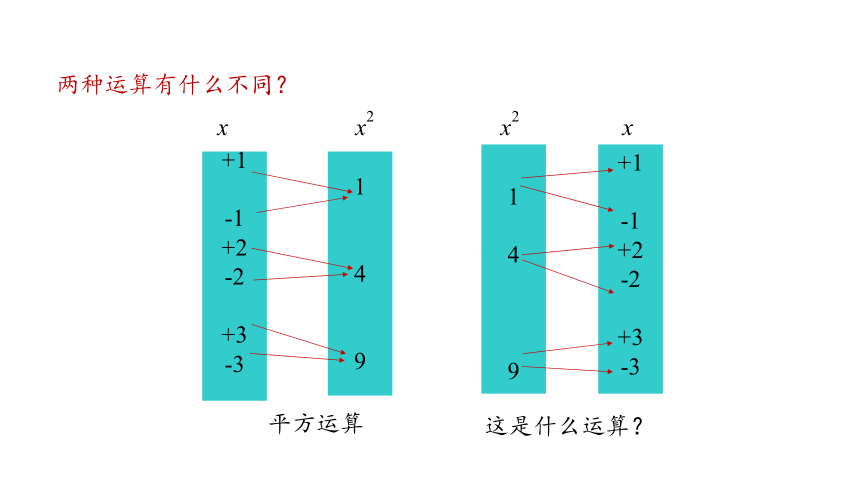
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
x x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2 x
求一个数的平方根的运算叫做开平方.
由上可知,开平方是平方的逆运算.根据这种关系,我们可以求出一些数的平方根.
平方与开平方有什么关系?
开平方的定义:
例1 判断下列各数是否有平方根,为什么?
25;;0.016 9;-64.
例题示范
解:因为正数和零都有平方根,负数没有平方根,所以25,,0.016 9都有平方根;-64没有平方根.
例2 求下列各数的平方根和算术平方根:
(1)1;(2)81;(3)64;(4)(-3) .
解:(1)因为(±1) =1,所以1的平方根是±1,即±=±1;1的算术平方根是1.
(2)因为(±9) =81,所以81的平方根是±9,即±=±9;81的算术平方根是9.
(3)因为(±8) =64,所以64的平方根是±8,即±=±8;64的算术平方根是8.
(4)(-3) =9.因为(±3) =9,所以9的平方根是±3,也就是(-3) 的平方根是±3,即±±3;(-3) 的算术平方根是3.
例3 利用计算器求下列各式的值(精确到0.01):
(1);(2);(3);(4).
解:(1)在计算器上依次键入:
(2)
(3)-
(4)在计算器上依次键入: ( 5 ÷ 7 ) =,
即可得
本章引言中提到的速度v2是第二宇宙速度,v2=
其中g取9.8 m/s ,r取6.4×106 m,用计算器可求得v2=
例4 跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作.如果不考虑空气阻力等其他因素影响,弹跳到最高点后,人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式:h=gr ,其h的单位是m,t的单位是s,g=9.8 m/s .假设跳板的高度是3 m,运动员在跳板上跳起至高出跳板1.2 m处开始下落,那么运动员下落到水面约需多长时间?
解:设运动员下落到水面约需t s,根据题意,得
3+1.2=×9.8t ,
t =
≈0.857 1,
t≈0.93.
因而,运动员下落到水面约需0.93 s.
随堂练习
A
1.(济宁·中考)4的算术平方根是( )
A. 2 B. -2
C. ±2 D. 4
2.若 1=0,则x的值是( )
A.-1 B.0
C.1 D.2
C
3.(中考·桂林)9的平方根是( )
A.3 B.±3
C.-3 D.9
4.某正数的两个不同的平方根是2a-1与-a+2,则这个数是( )
A.1 B.3
C.-3 D.9
D
B
5.下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
6.若方程(x-5)2=19的两根为a和b,且a>b,则下列结论中正确的是( )
A.a是19的算术平方根
B.b是19的平方根
C.a-5是19的算术平方根
D.b+5是19的平方根
C
1.若式子有意义,则x的取值范围是( )
A.x≥0
B.x≤2
C.x≥-2
D.x≥2
拓展提升
D
2.下列说法中不正确的有( )
①一个数的算术平方根一定是正数;
②100的算术平方根是10,记作=10;
③(3.14-π)2的算术平方根是3.14-π;
④a2的算术平方根为a;
⑤算术平方根不可能是负数.
A.2个 B.3个 C.4个 D.5个
B
3.若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4
B.8
C.±4
D.±8
4.一个正数的平方根分别是x+1和x-5,则x=______.
D
2
5.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
解:设每块地板砖的边长为x m.
由题意,得240x =60,即x =,
于是x==0.5.
所以,每块地板砖的边长是0.5 m.
归纳小结
平方根
平方根的概念
开平方及相关运算
平方根的性质
=a(a≥0).
1.算术平方根的概念,式子中的双重非负性:一是a≥0,二是≥0.
2.算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.
3.求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
第 6章 实数
6.1 平方根、立方根
1.平方根
初中数学七年级下册(HK版)
学习目标
1.了解平方根的概念,会表示一个数的平方根.
2.了解算术平方根的概念,会用根号表示一个正数的算术平方根.
3.了解平方和开方互为逆运算,会用平方运算求某些非负数的平方根.
4.会求一个正数的算术平方根,并解决实际问题.
学习重难点
1.了解平方根的概念,会表示一个数的平方根.
2.了解算术平方根的概念,会用根号表示一个正数的算术平方根.
1.了解平方和开方互为逆运算,会用平方运算求某些非负数的平方根.
2.会求一个正数的算术平方根,并解决实际问题.
难点
重点
创设情境
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1 m ,如图,问这种地砖一块的边长是多少?
知识点 平方根
新知引入
设一块正方形地砖的边长为x m,根据题意,有
x =
这是已知一个数的平方,求这个数的问题.
平方根的概念:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做二次方根.
例如,由于10 =100,(-10) =100,,所以100的平方根是+10和-10(可以合写为±10).
交流
1.16的平方根是什么? ±4
2.0的平方根是什么? 0
3.-9有没有平方根? 没有
一个正数a的平方根有两个,它们互为相反数.
我们用表示a的正的平方根,读作“根号a”,其中a叫做被开方数,这个根也叫做a的算术平方根,另一个负的平方根记为-.
0的平方根是0,0的算术平方根也是0,即=0.
负数没有平方根.
总结
中的a是一个非负数,a的算术平方根( )也是一个非负数,这也是算术平方根的性质——双重非负性.
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
x x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2 x
求一个数的平方根的运算叫做开平方.
由上可知,开平方是平方的逆运算.根据这种关系,我们可以求出一些数的平方根.
平方与开平方有什么关系?
开平方的定义:
例1 判断下列各数是否有平方根,为什么?
25;;0.016 9;-64.
例题示范
解:因为正数和零都有平方根,负数没有平方根,所以25,,0.016 9都有平方根;-64没有平方根.
例2 求下列各数的平方根和算术平方根:
(1)1;(2)81;(3)64;(4)(-3) .
解:(1)因为(±1) =1,所以1的平方根是±1,即±=±1;1的算术平方根是1.
(2)因为(±9) =81,所以81的平方根是±9,即±=±9;81的算术平方根是9.
(3)因为(±8) =64,所以64的平方根是±8,即±=±8;64的算术平方根是8.
(4)(-3) =9.因为(±3) =9,所以9的平方根是±3,也就是(-3) 的平方根是±3,即±±3;(-3) 的算术平方根是3.
例3 利用计算器求下列各式的值(精确到0.01):
(1);(2);(3);(4).
解:(1)在计算器上依次键入:
(2)
(3)-
(4)在计算器上依次键入: ( 5 ÷ 7 ) =,
即可得
本章引言中提到的速度v2是第二宇宙速度,v2=
其中g取9.8 m/s ,r取6.4×106 m,用计算器可求得v2=
例4 跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作.如果不考虑空气阻力等其他因素影响,弹跳到最高点后,人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式:h=gr ,其h的单位是m,t的单位是s,g=9.8 m/s .假设跳板的高度是3 m,运动员在跳板上跳起至高出跳板1.2 m处开始下落,那么运动员下落到水面约需多长时间?
解:设运动员下落到水面约需t s,根据题意,得
3+1.2=×9.8t ,
t =
≈0.857 1,
t≈0.93.
因而,运动员下落到水面约需0.93 s.
随堂练习
A
1.(济宁·中考)4的算术平方根是( )
A. 2 B. -2
C. ±2 D. 4
2.若 1=0,则x的值是( )
A.-1 B.0
C.1 D.2
C
3.(中考·桂林)9的平方根是( )
A.3 B.±3
C.-3 D.9
4.某正数的两个不同的平方根是2a-1与-a+2,则这个数是( )
A.1 B.3
C.-3 D.9
D
B
5.下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
6.若方程(x-5)2=19的两根为a和b,且a>b,则下列结论中正确的是( )
A.a是19的算术平方根
B.b是19的平方根
C.a-5是19的算术平方根
D.b+5是19的平方根
C
1.若式子有意义,则x的取值范围是( )
A.x≥0
B.x≤2
C.x≥-2
D.x≥2
拓展提升
D
2.下列说法中不正确的有( )
①一个数的算术平方根一定是正数;
②100的算术平方根是10,记作=10;
③(3.14-π)2的算术平方根是3.14-π;
④a2的算术平方根为a;
⑤算术平方根不可能是负数.
A.2个 B.3个 C.4个 D.5个
B
3.若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4
B.8
C.±4
D.±8
4.一个正数的平方根分别是x+1和x-5,则x=______.
D
2
5.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
解:设每块地板砖的边长为x m.
由题意,得240x =60,即x =,
于是x==0.5.
所以,每块地板砖的边长是0.5 m.
归纳小结
平方根
平方根的概念
开平方及相关运算
平方根的性质
=a(a≥0).
1.算术平方根的概念,式子中的双重非负性:一是a≥0,二是≥0.
2.算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.
3.求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
