6.2 实数 - 第2课时 - 实数的运算 课件(共22张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 6.2 实数 - 第2课时 - 实数的运算 课件(共22张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 798.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览






文档简介
第 6章 实数
6.2 实数
第2课时 - 实数的运算
初中数学七年级下册(HK版)
学习目标
1.理解在实数范围内的相反数、倒数、绝对值的意义.
2.掌握实数的运算法则,能进行简单的实数的运算及近似计算.
学习重难点
理解在实数范围内的相反数、倒数、绝对值的意义.
掌握实数的运算法则,能进行简单的实数的运算及近似计算.
难点
重点
回顾复习
1.实数的定义:有理数和无理数统称为实数.
2.实数的分类
(1)按定义分:
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
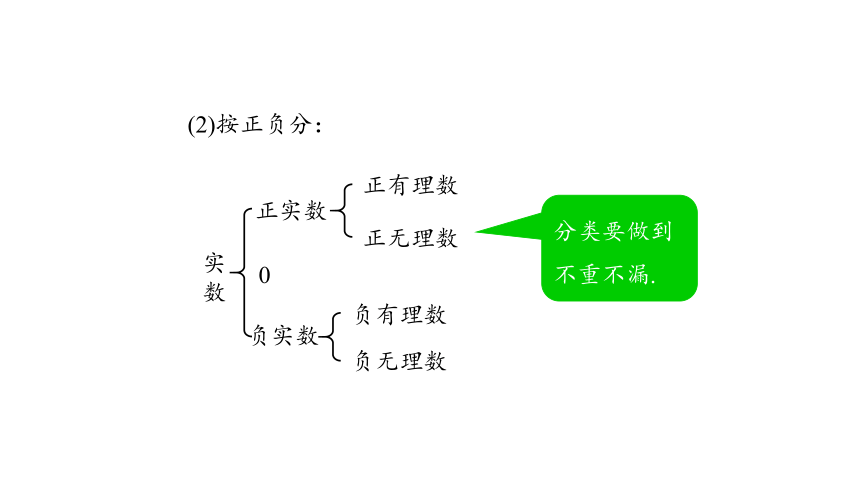
(2)按正负分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
分类要做到不重不漏.
创设情境
把有理数扩充到实数之后,有理数关于相反数和绝对值的意义同样适合于实数,进行实数的运算时,有理数的运算法则及运算性质等同样适用. 类比有理数的运算,如何进行实数的运算呢?
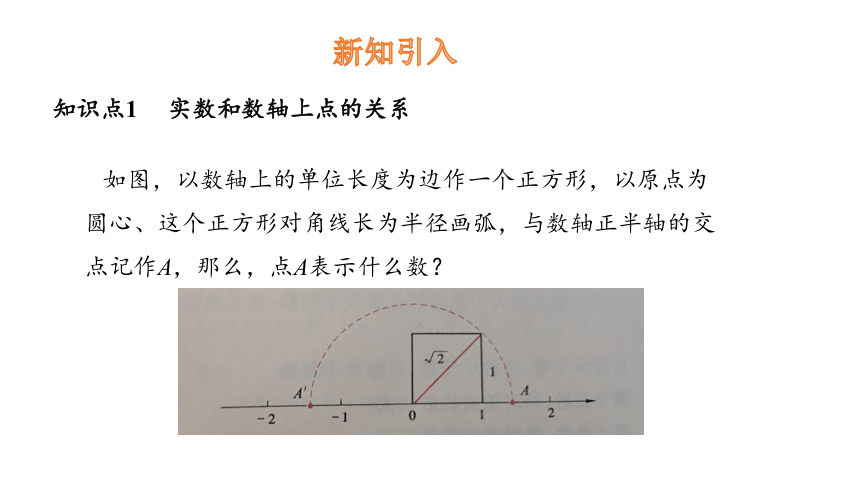
知识点1 实数和数轴上点的关系
新知引入
如图,以数轴上的单位长度为边作一个正方形,以原点为圆心、这个正方形对角线长为半径画弧,与数轴正半轴的交点记作A,那么,点A表示什么数?
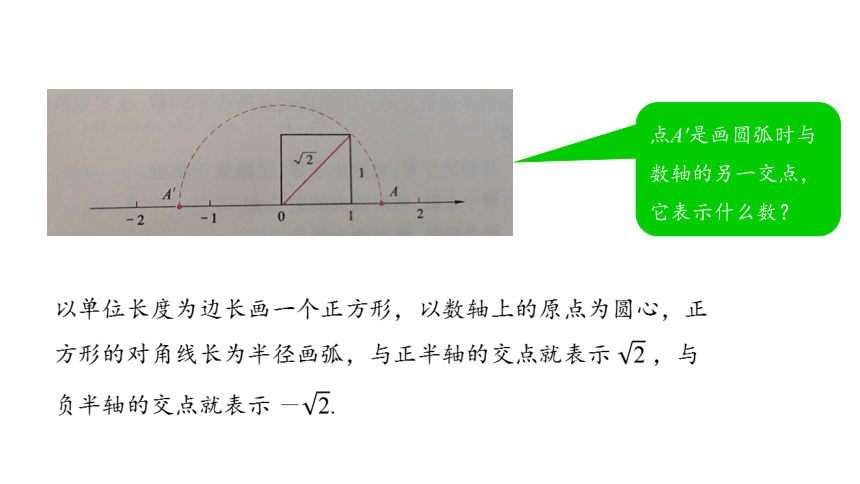
以单位长度为边长画一个正方形,以数轴上的原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点就表示 2 ,与负半轴的交点就表示?-2.
?
点A'是画圆弧时与数轴的另一交点,它表示什么数?
一般地,与有理数一样,每个无理数也都可以用数轴上的一个点来表示;反过来,数轴上的点不是表示无理数就是表示有理数.所以,把数从有理数扩充到实数以后,实数和数轴上的点一一对应,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
例题示范
例 (1)如图所示,OA=OB,数轴上点A对应的数是什么?它介于哪两个整数之间?
(2)如果将所有有理数标到数轴上,那么数轴被填满了吗?
(3)你能在数轴上找到5对应的点吗?与同伴进行交流.
?
解:(1)A点对应的数等于2 ,它介于1与2之间.
(2)如果将所有有理数都标到数轴上,数轴未被填满,在数轴上还可以表示无理数.
(3)构造直角边分别为2和1的直角三角形,斜边的长即为5 .
?
知识点2 实数的相反数、倒数、绝对值
新知引入
猜一猜:无理数的相反数、倒数、绝对值的意义是什么呢?
在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样.例如,2与-2互为相反数,有2+(-2)=0.
2与12互为倒数,有2×12=1.
任一实数a的绝对值仍然用|a|表示,如
|3|=3,|?3|=3.
?
实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对实数仍然适用.
例题示范
例 近似计算:
(1)3+π(精确到0.01);
(2)5×7(精确到0.1).
?
解:(1)3+π≈1.732+3.142=4.874≈1.87.
(2)5×7≈2.24×2.65=5.936≈5.9?.
?
知识点3 实数的大小比较
新知引入
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点表示的数.在实数范围内也有:
正数大于零,负数小于零,正数大于负数.
两个正数,绝对值大的数较大.
两个负数,绝对值大的数反而小.
例题示范
例 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
-1,2,-2,-2,|-22|,5.
?
解:
由数轴上各点的位置,得
-2<-2<-1<|-22|<5.
?
随堂练习
1.计算32-2的结果是( )
A.3 B. 2 C.22 D.42
2.估计(23+62)×13的值应在( )
A.4和5之间 B.5和6之间
C.6和7之间 D.7和8之间
?
C
C
3.(中考·恩施州)在实数范围内定义运算“☆”:a☆b=a+b-1,例如:2☆3=2+3-1=4.如果2☆x=1,则x的值是( )
A.-1 B.1
C.0 D.2
C
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1
B.-π-1
C.-π+1
D.π-1或-π-1
D
1.计算25-38的结果是( )
A.3 B.7 C.-3 D.-7
?
拓展提升
A
2.定义一个新运算,若i1=i,i2=-1,i3=-i,i4=1,i5=i,i6=-1,i7=-i,i8=1,…,则i2022=( )
A.-i B.i C.-1 D.1
C
【点拨】因为i1=i,i2=-1,i3=-i,i4=1,i5=i,i6=-1,i7=-i,i8=1,…,所以每4个数据一循环.因为2 022÷4=505……2,所以i2 022=i2=-1.故选C.
3.如图,两个实数互为相反数,在数轴上的对应点分别是点A、点B,则下列说法正确的是( )
A.原点在点A的左边
B.原点在线段AB的中点处
C.原点在点B的右边
D.原点可以在点A或点B上
B
4.已知a,b,c,d,e,f为实数,且a,b互为倒数,c,d互为相反数,e的绝对值为2,f的算术平方根是8,求12ab+????+????5+e2+3????的值.
?
解:因为a,b互为倒数,所以ab=1.
因为c,d互为相反数,所以c+d=0.
因为|e|=2,所以e2=2.
因为3????=8,所以f=64.
所以原式=12×1+0+2+364=132.
?
归纳小结
1.在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样.
2.实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对实数仍然适用.
3. 两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点表示的数.在实数范围内也有:正数大于零,负数小于零,正数大于负数.两个正数,绝对值大的数较大.两个负数,绝对值大的数反而小.
6.2 实数
第2课时 - 实数的运算
初中数学七年级下册(HK版)
学习目标
1.理解在实数范围内的相反数、倒数、绝对值的意义.
2.掌握实数的运算法则,能进行简单的实数的运算及近似计算.
学习重难点
理解在实数范围内的相反数、倒数、绝对值的意义.
掌握实数的运算法则,能进行简单的实数的运算及近似计算.
难点
重点
回顾复习
1.实数的定义:有理数和无理数统称为实数.
2.实数的分类
(1)按定义分:
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
(2)按正负分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
分类要做到不重不漏.
创设情境
把有理数扩充到实数之后,有理数关于相反数和绝对值的意义同样适合于实数,进行实数的运算时,有理数的运算法则及运算性质等同样适用. 类比有理数的运算,如何进行实数的运算呢?
知识点1 实数和数轴上点的关系
新知引入
如图,以数轴上的单位长度为边作一个正方形,以原点为圆心、这个正方形对角线长为半径画弧,与数轴正半轴的交点记作A,那么,点A表示什么数?
以单位长度为边长画一个正方形,以数轴上的原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点就表示 2 ,与负半轴的交点就表示?-2.
?
点A'是画圆弧时与数轴的另一交点,它表示什么数?
一般地,与有理数一样,每个无理数也都可以用数轴上的一个点来表示;反过来,数轴上的点不是表示无理数就是表示有理数.所以,把数从有理数扩充到实数以后,实数和数轴上的点一一对应,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
例题示范
例 (1)如图所示,OA=OB,数轴上点A对应的数是什么?它介于哪两个整数之间?
(2)如果将所有有理数标到数轴上,那么数轴被填满了吗?
(3)你能在数轴上找到5对应的点吗?与同伴进行交流.
?
解:(1)A点对应的数等于2 ,它介于1与2之间.
(2)如果将所有有理数都标到数轴上,数轴未被填满,在数轴上还可以表示无理数.
(3)构造直角边分别为2和1的直角三角形,斜边的长即为5 .
?
知识点2 实数的相反数、倒数、绝对值
新知引入
猜一猜:无理数的相反数、倒数、绝对值的意义是什么呢?
在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样.例如,2与-2互为相反数,有2+(-2)=0.
2与12互为倒数,有2×12=1.
任一实数a的绝对值仍然用|a|表示,如
|3|=3,|?3|=3.
?
实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对实数仍然适用.
例题示范
例 近似计算:
(1)3+π(精确到0.01);
(2)5×7(精确到0.1).
?
解:(1)3+π≈1.732+3.142=4.874≈1.87.
(2)5×7≈2.24×2.65=5.936≈5.9?.
?
知识点3 实数的大小比较
新知引入
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点表示的数.在实数范围内也有:
正数大于零,负数小于零,正数大于负数.
两个正数,绝对值大的数较大.
两个负数,绝对值大的数反而小.
例题示范
例 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
-1,2,-2,-2,|-22|,5.
?
解:
由数轴上各点的位置,得
-2<-2<-1<|-22|<5.
?
随堂练习
1.计算32-2的结果是( )
A.3 B. 2 C.22 D.42
2.估计(23+62)×13的值应在( )
A.4和5之间 B.5和6之间
C.6和7之间 D.7和8之间
?
C
C
3.(中考·恩施州)在实数范围内定义运算“☆”:a☆b=a+b-1,例如:2☆3=2+3-1=4.如果2☆x=1,则x的值是( )
A.-1 B.1
C.0 D.2
C
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1
B.-π-1
C.-π+1
D.π-1或-π-1
D
1.计算25-38的结果是( )
A.3 B.7 C.-3 D.-7
?
拓展提升
A
2.定义一个新运算,若i1=i,i2=-1,i3=-i,i4=1,i5=i,i6=-1,i7=-i,i8=1,…,则i2022=( )
A.-i B.i C.-1 D.1
C
【点拨】因为i1=i,i2=-1,i3=-i,i4=1,i5=i,i6=-1,i7=-i,i8=1,…,所以每4个数据一循环.因为2 022÷4=505……2,所以i2 022=i2=-1.故选C.
3.如图,两个实数互为相反数,在数轴上的对应点分别是点A、点B,则下列说法正确的是( )
A.原点在点A的左边
B.原点在线段AB的中点处
C.原点在点B的右边
D.原点可以在点A或点B上
B
4.已知a,b,c,d,e,f为实数,且a,b互为倒数,c,d互为相反数,e的绝对值为2,f的算术平方根是8,求12ab+????+????5+e2+3????的值.
?
解:因为a,b互为倒数,所以ab=1.
因为c,d互为相反数,所以c+d=0.
因为|e|=2,所以e2=2.
因为3????=8,所以f=64.
所以原式=12×1+0+2+364=132.
?
归纳小结
1.在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样.
2.实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对实数仍然适用.
3. 两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点表示的数.在实数范围内也有:正数大于零,负数小于零,正数大于负数.两个正数,绝对值大的数较大.两个负数,绝对值大的数反而小.
