8.1.1 幂的运算-----同底数幂的乘法 课件 (共20张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.1.1 幂的运算-----同底数幂的乘法 课件 (共20张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:52:12 | ||
图片预览






文档简介
(共20张PPT)
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.1 同底数幂的乘法
学习目标
1.理解并掌握幂的运算性质1(同底数幂的乘法).(重点)
2.运用同底数幂的乘法法则进行相关运算.(难点)
3.经历探索同底数幂的乘法法则的过程,进一步体会幂的意义,提高推理能力和有条理的表达能力.
知识回顾
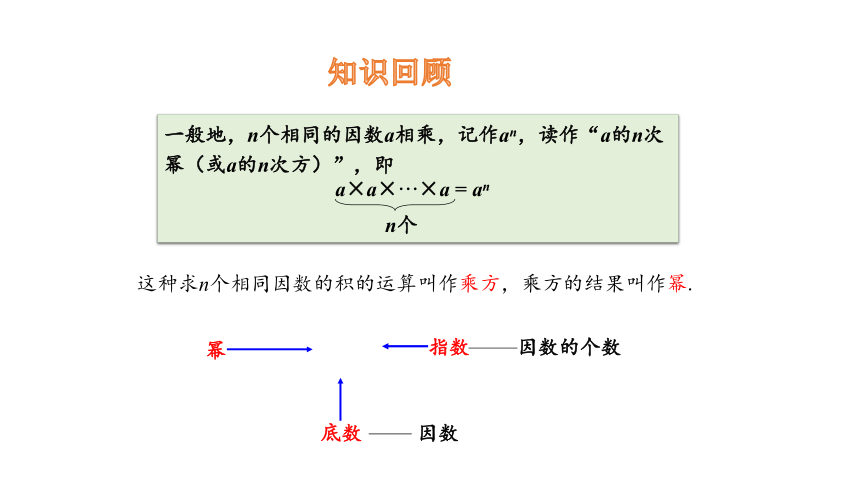
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a×a×···×a = an
n个
这种求n个相同因数的积的运算叫作乘方,乘方的结果叫作幂.
幂
指数
因数的个数
底数
因数
回顾有理数的乘方,计算:
101=___, 102=____,103=______,104=_______,
106=__________,1010=_______________,…
知识回顾
10
100
1 000
10 000
1 000 000
10 000 000 000
用科学记数法表示数
你观察到什么规律?
1.10的几次幂就等于1后面有几个0.
2.运算结果的位数比指数大1.
情境导入
我国首台千万亿次超级计算机系统“天河一号3计算机每秒可进行2.57×1015次运算,问它工作1h(3.6×10 s)可进行多少次运算?
分析:已知每秒进行运算的次数及时间,求总的运算次数.
2.57×1015×3.6×103 =2.57×3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
思 考
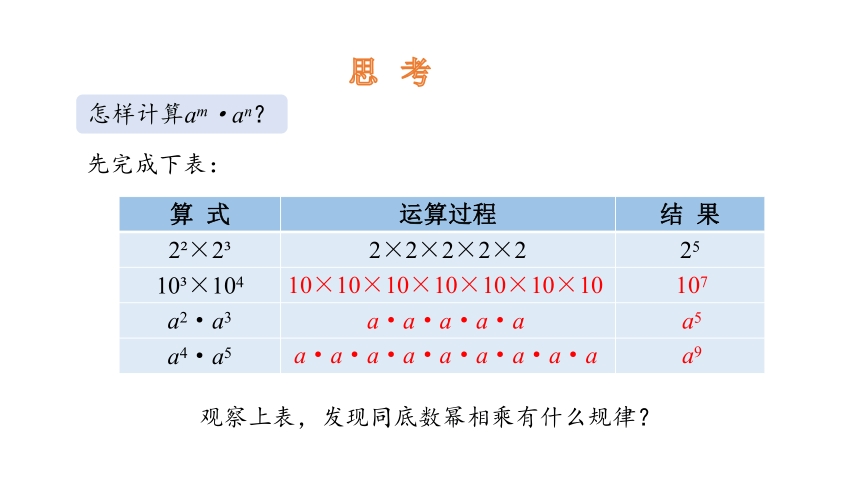
怎样计算am·an?
先完成下表:
算 式 运算过程 结 果
2 ×2 2×2×2×2×2 25
10 ×104
a2·a3
a4·a5
10×10×10×10×10×10×10
107
a·a·a·a·a
a5
a·a·a·a·a·a·a·a·a
a9
观察上表,发现同底数幂相乘有什么规律?
一般地,如果字母m,n都是正整数,那么
新课讲授
同底数幂的乘法
(根据___________.)
(根据 .)
=(a·a·…·a)(a·a·…·a)
m个
n个
=(a·a·…·a)
(m+n)个
= am+n.
幂的意义
幂的意义
(根据 .)
乘法结合律
am·an
幂的运算性质1
知识拓展
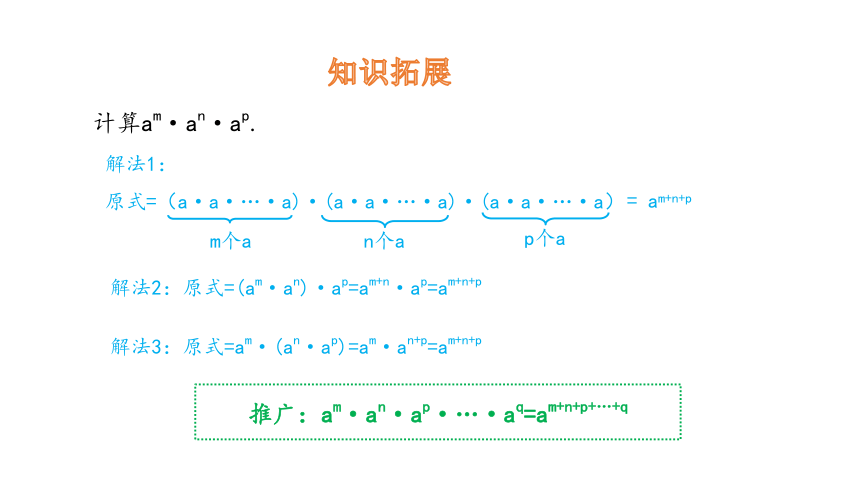
计算am·an·ap.
解法2:原式=(am·an)·ap=am+n·ap=am+n+p
解法3:原式=am·(an·ap)=am·an+p=am+n+p
解法1:
原式=(a·a·…·a)·(a·a·…·a)·(a·a·…·a)
m个a
n个a
= am+n+p
p个a
推广:am·an·ap·…·aq=am+n+p+…+q
教材例题
例.计算:
(1)5×8;
=(××…×)×(××…×)
5个
8个
= ××…×
(5+8)个
= 13
= 5+8
= 13.
例.计算:
(2)2×7;
=[(-2)×(-2)]×[(-3)×(-3)×…×(-3)]
2个
7个
=(-2)×(-2)×…×(-2)
(2+7)个
=(-2)9
=(-2)2+7
=(-2)9
教材例题
例.计算:
(3)a ·a ·a6;
=a·a·…·a
(2+3+6)个
=a11
=(a·a)·(a·a·a)·(a·a·a·a·a·a)
2个
3个
6个
=a2+3+6
=a11
教材例题
例.计算:
(4)(-y)3·y4·a6;
=-y ·y4
(3+4)个
=-y7
=[(-y)·(-y)·(-y)]·(y·y·y·y)
3个(-y)
4个y
=-y3+4
=-y7
教材例题
例1. 计算:
(1)3×;(2)7×5;(3)b2m·b2m+1(m是正整数).
解:(1)3×=3+1=4;
(2)7×5=7+5=12;
(3)b2m·b2m+1=b2m+(2m+1)=b4m+1.
例题解读
例题解读
例2 光的速度约为3×105千米/秒,太阳光照射到地球上大约需要5×102秒,地球距离太阳大约有多远 (结果用科学记数法表示)
解:根据“路程=速度×时间”可得
3×105×5×102=15×107(km).
15×107=1.5×108
地球距离太阳大约有1.5×108km.
例3 计算(a-b)2n·(b-a)·(a-b)m-1的结果是( )
A.(a-b)2n+m B.-(a-b)2n+m
C.(b-a)2n+m D.以上都不对
例题解读
解析:b-a=-(a-b).
原式=(a-b)2n ·[-(a-b)]·(a-b)m-1
=-(a-b)2n·(a-b)·(a-b)m-1
=-(a-b)2n+1+m-1
=-(a-b)2n+m.
注意
①系数相乘时,不要漏乘(a-b)前面的(-1);
②指数相加时,不要漏加(a-b)的指数1.
B
x3·x5=x15 ( ) (2)x·x3=x3 ( )
(3)x3+x5=x8 ( ) (4)x2·x2=2x4 ( )
(5)(-x)2 ·(-x)3 =(-x)5=-x5 ( ) (6)a3·a2 - a2·a3 =0 ( )
(7)a3·b5=(ab)8 ( ) (8)y7+y7=y14 ( )
随堂练习
1.判断(正确的打“√”,错误的打“×”,并改正)
√
√
×
×
×
×
×
×
改正:x8
改正:x4
不能合并
改正:a3b5
改正:x4
改正:2y7
随堂练习
3.若m为偶数,则(a-b)m·(b-a)n与(b-a)m+n的结果( )
A.相等 B.互为相反数
C.不相等 D.以上说法都不对
4.(云南中考)按一定规律排列的单项式:a,-2a,4a,-8a,
16a,-32a,….第n个单项式是( )
A.(-2)n-1 a B.(-2)na
C.2n-1 a D.2na
随堂练习
A
A
随堂练习
5.已知我国平均每平方千米的土地上,一年内从太阳得到的能量相当于燃烧 1.3×108千克煤所产生的能量,那么我国山东省约15.58万平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤所产生的能量?
课时小结
幂的运算性质1——同底数幂的乘法
同底数幂相乘,底数不变,指数相加.
am·an
= am+n
(m,n都是正整数)
推广:am·an·ap·…·aq=am+n+p+…+q
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.1 同底数幂的乘法
学习目标
1.理解并掌握幂的运算性质1(同底数幂的乘法).(重点)
2.运用同底数幂的乘法法则进行相关运算.(难点)
3.经历探索同底数幂的乘法法则的过程,进一步体会幂的意义,提高推理能力和有条理的表达能力.
知识回顾
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a×a×···×a = an
n个
这种求n个相同因数的积的运算叫作乘方,乘方的结果叫作幂.
幂
指数
因数的个数
底数
因数
回顾有理数的乘方,计算:
101=___, 102=____,103=______,104=_______,
106=__________,1010=_______________,…
知识回顾
10
100
1 000
10 000
1 000 000
10 000 000 000
用科学记数法表示数
你观察到什么规律?
1.10的几次幂就等于1后面有几个0.
2.运算结果的位数比指数大1.
情境导入
我国首台千万亿次超级计算机系统“天河一号3计算机每秒可进行2.57×1015次运算,问它工作1h(3.6×10 s)可进行多少次运算?
分析:已知每秒进行运算的次数及时间,求总的运算次数.
2.57×1015×3.6×103 =2.57×3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
思 考
怎样计算am·an?
先完成下表:
算 式 运算过程 结 果
2 ×2 2×2×2×2×2 25
10 ×104
a2·a3
a4·a5
10×10×10×10×10×10×10
107
a·a·a·a·a
a5
a·a·a·a·a·a·a·a·a
a9
观察上表,发现同底数幂相乘有什么规律?
一般地,如果字母m,n都是正整数,那么
新课讲授
同底数幂的乘法
(根据___________.)
(根据 .)
=(a·a·…·a)(a·a·…·a)
m个
n个
=(a·a·…·a)
(m+n)个
= am+n.
幂的意义
幂的意义
(根据 .)
乘法结合律
am·an
幂的运算性质1
知识拓展
计算am·an·ap.
解法2:原式=(am·an)·ap=am+n·ap=am+n+p
解法3:原式=am·(an·ap)=am·an+p=am+n+p
解法1:
原式=(a·a·…·a)·(a·a·…·a)·(a·a·…·a)
m个a
n个a
= am+n+p
p个a
推广:am·an·ap·…·aq=am+n+p+…+q
教材例题
例.计算:
(1)5×8;
=(××…×)×(××…×)
5个
8个
= ××…×
(5+8)个
= 13
= 5+8
= 13.
例.计算:
(2)2×7;
=[(-2)×(-2)]×[(-3)×(-3)×…×(-3)]
2个
7个
=(-2)×(-2)×…×(-2)
(2+7)个
=(-2)9
=(-2)2+7
=(-2)9
教材例题
例.计算:
(3)a ·a ·a6;
=a·a·…·a
(2+3+6)个
=a11
=(a·a)·(a·a·a)·(a·a·a·a·a·a)
2个
3个
6个
=a2+3+6
=a11
教材例题
例.计算:
(4)(-y)3·y4·a6;
=-y ·y4
(3+4)个
=-y7
=[(-y)·(-y)·(-y)]·(y·y·y·y)
3个(-y)
4个y
=-y3+4
=-y7
教材例题
例1. 计算:
(1)3×;(2)7×5;(3)b2m·b2m+1(m是正整数).
解:(1)3×=3+1=4;
(2)7×5=7+5=12;
(3)b2m·b2m+1=b2m+(2m+1)=b4m+1.
例题解读
例题解读
例2 光的速度约为3×105千米/秒,太阳光照射到地球上大约需要5×102秒,地球距离太阳大约有多远 (结果用科学记数法表示)
解:根据“路程=速度×时间”可得
3×105×5×102=15×107(km).
15×107=1.5×108
地球距离太阳大约有1.5×108km.
例3 计算(a-b)2n·(b-a)·(a-b)m-1的结果是( )
A.(a-b)2n+m B.-(a-b)2n+m
C.(b-a)2n+m D.以上都不对
例题解读
解析:b-a=-(a-b).
原式=(a-b)2n ·[-(a-b)]·(a-b)m-1
=-(a-b)2n·(a-b)·(a-b)m-1
=-(a-b)2n+1+m-1
=-(a-b)2n+m.
注意
①系数相乘时,不要漏乘(a-b)前面的(-1);
②指数相加时,不要漏加(a-b)的指数1.
B
x3·x5=x15 ( ) (2)x·x3=x3 ( )
(3)x3+x5=x8 ( ) (4)x2·x2=2x4 ( )
(5)(-x)2 ·(-x)3 =(-x)5=-x5 ( ) (6)a3·a2 - a2·a3 =0 ( )
(7)a3·b5=(ab)8 ( ) (8)y7+y7=y14 ( )
随堂练习
1.判断(正确的打“√”,错误的打“×”,并改正)
√
√
×
×
×
×
×
×
改正:x8
改正:x4
不能合并
改正:a3b5
改正:x4
改正:2y7
随堂练习
3.若m为偶数,则(a-b)m·(b-a)n与(b-a)m+n的结果( )
A.相等 B.互为相反数
C.不相等 D.以上说法都不对
4.(云南中考)按一定规律排列的单项式:a,-2a,4a,-8a,
16a,-32a,….第n个单项式是( )
A.(-2)n-1 a B.(-2)na
C.2n-1 a D.2na
随堂练习
A
A
随堂练习
5.已知我国平均每平方千米的土地上,一年内从太阳得到的能量相当于燃烧 1.3×108千克煤所产生的能量,那么我国山东省约15.58万平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤所产生的能量?
课时小结
幂的运算性质1——同底数幂的乘法
同底数幂相乘,底数不变,指数相加.
am·an
= am+n
(m,n都是正整数)
推广:am·an·ap·…·aq=am+n+p+…+q
