8.1.2(2) 幂的运算-----幂的乘方与积的乘方 课件 (共16张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.1.2(2) 幂的运算-----幂的乘方与积的乘方 课件 (共16张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 20:57:25 | ||
图片预览





文档简介
(共16张PPT)
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.2 幂的乘方与积的乘方
第2课时 积的乘方
学习目标
1.会推导积的乘方法则,并能运用幂的运算性质3(积的乘方)进行有关计算.(重点、难点)
2.经历探索积的乘方的运算性质的过程,进一步体会幂运算的意义.
知识回顾
幂的乘方运算法则:
(am)n=amn
(m,n都是正整数)
幂的意义:
a×a×···×a = an
n个
幂同底数幂的乘法法则:
am·an=am+n(m,n都是正整数)
情境导入
地球可以近似地看做是球体,地球的半径约为6.4×10 km,它的体积大约是多少立方千米 (π取3.14)
球的体积公式是,
其中V是体积,r是球的半径.
地球的体积是
×3.14×(6.4×10 ) .
等于多少呢?
思 考
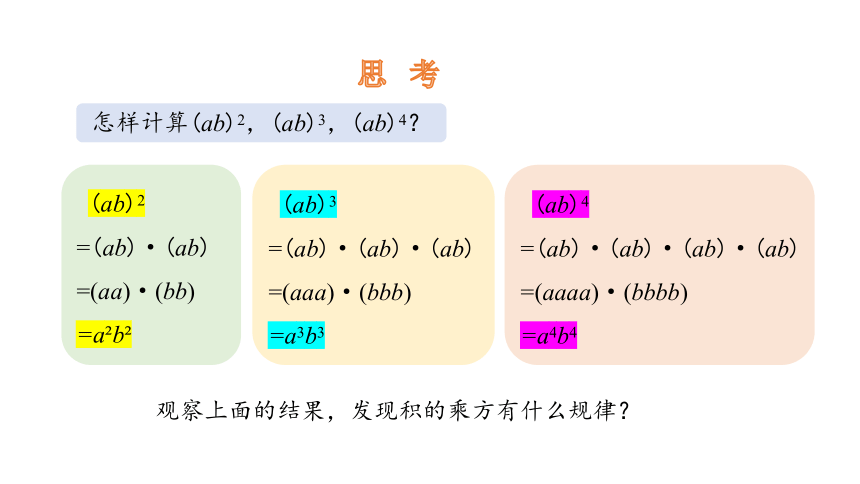
怎样计算(ab)2,(ab)3,(ab)4?
(ab)2
=(ab)·(ab)
=(aa)·(bb)
=a b
观察上面的结果,发现积的乘方有什么规律?
(ab)3
=(ab)·(ab)·(ab)
=(aaa)·(bbb)
=a3b3
(ab)4
=(ab)·(ab)·(ab)·(ab)
=(aaaa)·(bbbb)
=a4b4
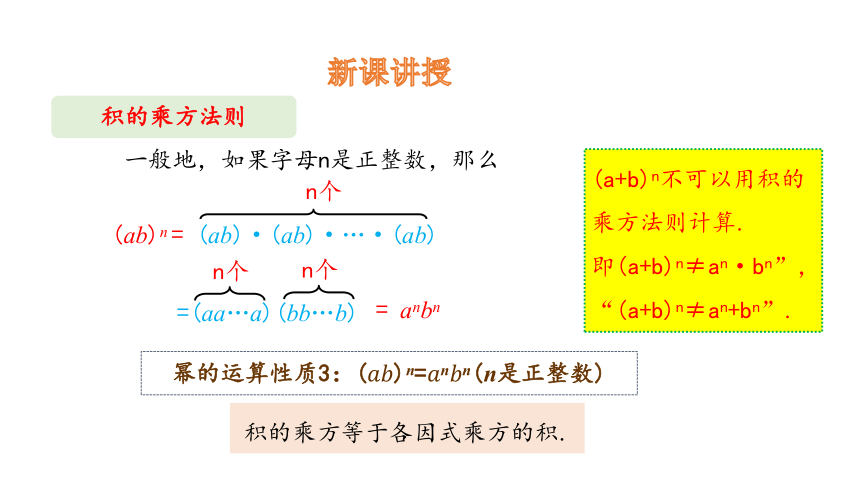
新课讲授
积的乘方法则
幂的运算性质3:()n=nn(n是正整数)
积的乘方等于各因式乘方的积.
(a+b)n不可以用积的乘方法则计算.
即(a+b)n≠an·bn”,“(a+b)n≠an+bn”.
一般地,如果字母n是正整数,那么
= anbn
(ab)n = (ab)·(ab)·…·(ab)
n个
=(aa…a)(bb…b)
n个
n个
教材例题
例 计算:
(1)(2x)4 ; (2)(-3ab c )2.
(2x)4
=(2x)·(2x)·(2x)·(2x)
=(2×2×2×2)·(x·x·x·x)
=24x4=16x4
(-3ab c )2
=(-3ab c )·(-3ab c )
=(-3) ·(a) ·(b ) ·(c3)
=9a3b4c6
教材例题
地球可以近似地看做是球体,地球的半径约为6.4×10 km,它的体积大约是多少立方千米 (π取3.14)
地球的体积是
×3.14×(6.4×10 )
=×3.14×6.43×109
≈1.1×1012(km3)
例题解读
(1)(3×5)4=3( )×5( ); (2)(3×5)m=3( )×5( );
(3×5)4
=(3×5)×(3×5)×(3×5)×(3×5)
=(3×3×3×3)×(5×5×5×5)
=34×54.
幂的意义
乘法交换律、结合律
幂的意义
4
4
(3×5)m
=(3×5)×(3×5)×…×(3×5)
=(3×3×…×3)×(5×5×…×5)
=3m×5m.
幂的意义
乘法交换律、结合律
幂的意义
m个(3×5)
m个3
m个5
m
m
例1 计算:
例题解读
例2 计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 .
=32x2
=9x2;
(1)(3x)2
解:
(2)(-2b)5
= (-2)5b5
=-32b5;
(3)(-2xy)4
= (-2x)4 y4
=(-2)4 x4 y4
=16x4 y4;
例题解读
例3 计算:x3 · x5 + (x2)4 +(-2x4)2.
x3·x5 + (x2)4 +(-2x4)2
解:
=x8+x8+4x8
=6x8
①同底数幂的乘法;
②幂的乘方;
③积的乘方.
①
②
③
④合并同类项.
④
知识拓展
三个或三个以上的积的乘方,是否也具有上面的性质 (abc)n等于什么?
(abc)n=an·bn·cn
证明:
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
三个或三个以上的积的乘方,也具有上面的性质.
乘法结合律
积的乘方
积的乘方
随堂练习
1.计算(-x2)3的结果是( )
(A)-x5 (B)x5 (C)-x6 (D)x6
2.下列四个算式中,正确的算式有( )
①(a3)3=a3+3=a6; ②[(b2)2]2=b8;
③[(-x)3]4=(-x)12=x12; ④(-y2)5=y10.
(A)0个 (B)1个 (C)2个 (D)3个
C
√
√
C
(1)-2a6-(-3a ) ; (4)(x y6)n+(-2xny2n) ;
(2)a ·a5++(a )4+(-3a4) ; (5)[(x ) ] -3(x ·x ·x) .
(3)(-2anb3n) +(a b6)n;
随堂练习
3.计算:
随堂练习
4.(1)已知an=2,b2n=3,求(a3b4)2n的值.
解:原式=a6nb8n=(an)6(b2n)4=26×34=5 184.
(2)若59=a,95=b,用a,b表示4545的值.
解:因为a5=(59)5=545,b9=(95)9=945,
所以4545=(5×9)45=545×945=a5b9.
课时小结
幂的运算性质2——幂的乘方
(am)n=amn
(m,n都是正整数)
①幂的乘方法则的逆用:amn=(am)n=(an)m.
②积的乘方法则的逆用:anbn=(ab)n.
幂的运算性质3——积的乘方
(ab)n=anbn
(n是正整数)
幂的运算性质1——同底数幂的乘法
am·an
=am+n
(m,n都是正整数)
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.2 幂的乘方与积的乘方
第2课时 积的乘方
学习目标
1.会推导积的乘方法则,并能运用幂的运算性质3(积的乘方)进行有关计算.(重点、难点)
2.经历探索积的乘方的运算性质的过程,进一步体会幂运算的意义.
知识回顾
幂的乘方运算法则:
(am)n=amn
(m,n都是正整数)
幂的意义:
a×a×···×a = an
n个
幂同底数幂的乘法法则:
am·an=am+n(m,n都是正整数)
情境导入
地球可以近似地看做是球体,地球的半径约为6.4×10 km,它的体积大约是多少立方千米 (π取3.14)
球的体积公式是,
其中V是体积,r是球的半径.
地球的体积是
×3.14×(6.4×10 ) .
等于多少呢?
思 考
怎样计算(ab)2,(ab)3,(ab)4?
(ab)2
=(ab)·(ab)
=(aa)·(bb)
=a b
观察上面的结果,发现积的乘方有什么规律?
(ab)3
=(ab)·(ab)·(ab)
=(aaa)·(bbb)
=a3b3
(ab)4
=(ab)·(ab)·(ab)·(ab)
=(aaaa)·(bbbb)
=a4b4
新课讲授
积的乘方法则
幂的运算性质3:()n=nn(n是正整数)
积的乘方等于各因式乘方的积.
(a+b)n不可以用积的乘方法则计算.
即(a+b)n≠an·bn”,“(a+b)n≠an+bn”.
一般地,如果字母n是正整数,那么
= anbn
(ab)n = (ab)·(ab)·…·(ab)
n个
=(aa…a)(bb…b)
n个
n个
教材例题
例 计算:
(1)(2x)4 ; (2)(-3ab c )2.
(2x)4
=(2x)·(2x)·(2x)·(2x)
=(2×2×2×2)·(x·x·x·x)
=24x4=16x4
(-3ab c )2
=(-3ab c )·(-3ab c )
=(-3) ·(a) ·(b ) ·(c3)
=9a3b4c6
教材例题
地球可以近似地看做是球体,地球的半径约为6.4×10 km,它的体积大约是多少立方千米 (π取3.14)
地球的体积是
×3.14×(6.4×10 )
=×3.14×6.43×109
≈1.1×1012(km3)
例题解读
(1)(3×5)4=3( )×5( ); (2)(3×5)m=3( )×5( );
(3×5)4
=(3×5)×(3×5)×(3×5)×(3×5)
=(3×3×3×3)×(5×5×5×5)
=34×54.
幂的意义
乘法交换律、结合律
幂的意义
4
4
(3×5)m
=(3×5)×(3×5)×…×(3×5)
=(3×3×…×3)×(5×5×…×5)
=3m×5m.
幂的意义
乘法交换律、结合律
幂的意义
m个(3×5)
m个3
m个5
m
m
例1 计算:
例题解读
例2 计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 .
=32x2
=9x2;
(1)(3x)2
解:
(2)(-2b)5
= (-2)5b5
=-32b5;
(3)(-2xy)4
= (-2x)4 y4
=(-2)4 x4 y4
=16x4 y4;
例题解读
例3 计算:x3 · x5 + (x2)4 +(-2x4)2.
x3·x5 + (x2)4 +(-2x4)2
解:
=x8+x8+4x8
=6x8
①同底数幂的乘法;
②幂的乘方;
③积的乘方.
①
②
③
④合并同类项.
④
知识拓展
三个或三个以上的积的乘方,是否也具有上面的性质 (abc)n等于什么?
(abc)n=an·bn·cn
证明:
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
三个或三个以上的积的乘方,也具有上面的性质.
乘法结合律
积的乘方
积的乘方
随堂练习
1.计算(-x2)3的结果是( )
(A)-x5 (B)x5 (C)-x6 (D)x6
2.下列四个算式中,正确的算式有( )
①(a3)3=a3+3=a6; ②[(b2)2]2=b8;
③[(-x)3]4=(-x)12=x12; ④(-y2)5=y10.
(A)0个 (B)1个 (C)2个 (D)3个
C
√
√
C
(1)-2a6-(-3a ) ; (4)(x y6)n+(-2xny2n) ;
(2)a ·a5++(a )4+(-3a4) ; (5)[(x ) ] -3(x ·x ·x) .
(3)(-2anb3n) +(a b6)n;
随堂练习
3.计算:
随堂练习
4.(1)已知an=2,b2n=3,求(a3b4)2n的值.
解:原式=a6nb8n=(an)6(b2n)4=26×34=5 184.
(2)若59=a,95=b,用a,b表示4545的值.
解:因为a5=(59)5=545,b9=(95)9=945,
所以4545=(5×9)45=545×945=a5b9.
课时小结
幂的运算性质2——幂的乘方
(am)n=amn
(m,n都是正整数)
①幂的乘方法则的逆用:amn=(am)n=(an)m.
②积的乘方法则的逆用:anbn=(ab)n.
幂的运算性质3——积的乘方
(ab)n=anbn
(n是正整数)
幂的运算性质1——同底数幂的乘法
am·an
=am+n
(m,n都是正整数)
