8.1.3(2) 幂的运算---零指数幂与负整数指数幂 课件(2课时,共30张ppt) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.1.3(2) 幂的运算---零指数幂与负整数指数幂 课件(2课时,共30张ppt) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览










文档简介
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.3 同底数幂的除法
第2课时 零次幂与负整数次幂
学习目标
1.理解零次幂和负整数指数幂的概念及性质.
2.会熟练进行零次幂和负整数指数幂的运算.(重点、难点)
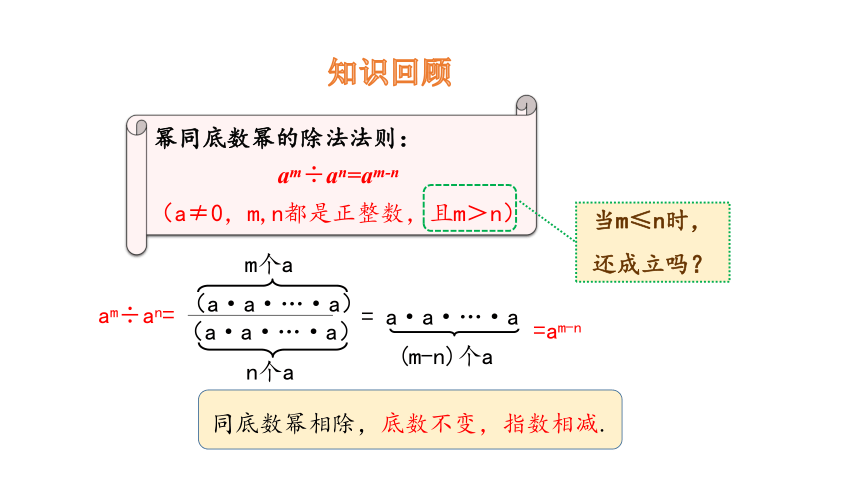
知识回顾
幂同底数幂的除法法则:
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减.
当m≤n时,
还成立吗?
= a·a·…·a
(m-n)个a
am÷an=
=am-n
(a·a·…·a)
(a·a·…·a)
m个a
n个a
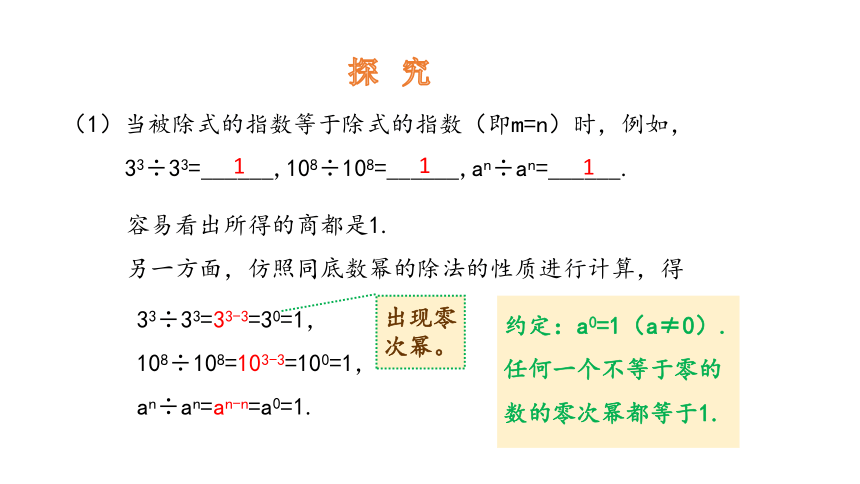
探 究
(1)当被除式的指数等于除式的指数(即m=n)时,例如,
33÷33=______,108÷108=______,an÷an=______.
1
1
1
容易看出所得的商都是1.
另一方面,仿照同底数幂的除法的性质进行计算,得
33÷33=33-3=30=1,
108÷108=103-3=100=1,
an÷an=an-n=a0=1.
出现零次幂。
约定:a0=1(a≠0).
任何一个不等于零的数的零次幂都等于1.
探 究
(2)当被除式的指数小于除式的指数(即m<n)时,例如,
32÷35=______,104÷108=______,am÷an=___________.
那么可以通过分数约分,得
32÷35=3?35=3?3?×3?=13?,
?
104÷108=104108=104104×104=1104,
?
am÷an=????????????????=1?????????
探 究
(2)当被除式的指数小于除式的指数(即m<n)时,例如,
32÷35=______,104÷108=______,am÷an=______________.
另一方面,仿照同底数幂的除法的性质进行计算,得
32÷35=32-5=3-3,104÷108=104-8=10-4,
am÷an=am-n=a-p.(p=n-m)
3-3 10-4 a-p(p=n-m)
出现负整数次幂。
约定:a-p=????????????(a≠0,p是正整数).任何一个不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数.
?
幂同底数幂的除法法则:
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
归纳总结
当m≤n时,也成立.
规定:a0=1(a≠0);a-p=1????p(a≠0,p是正整数).
即任何一个不等于零的数,它的零次幂等于1,
它的-p(p是正整数)次幂等于这个数的p次幂的倒数.
?
教材例题
例 计算:
(1)106÷106; (2)(17)0÷(17)-2; (3)(-2)3÷(-2)5.
?
解:(1)106÷106=106?6=100=1.
?
(2)(17)0÷(17)?2=(17)0?(?2)=(17)2=149.
?
(3)(-2)3÷(-2)5=(?2)3?5=(?2)?2=1(?2)?=14.
?
例题解读
例1 用小数或分数表示下列各数:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
解:(1)10-3=110?=11?000=0.001.
?
(2)70×8-2=1×18?=164.
?
(3)1.6×10-4=1.6×1104=1.6×0.000?1=0.000?16.
?
例题解读
例2 下列各式的计算中,不正确的个数是( )
①100÷10-1=10; ②10-4×(2×7)0=10 000;
③(-0.1)0÷(-2-1)-3=8; ④(-10)-4÷(-10-1)-4=-1.
A.4 B.3 C.2 D.1
解析:①100÷10-1=1÷110=10,正确;
②10-4×(2×7)0=1104×1=0.000 1,不正确;
③(-0.1)0÷(-2-1)-3=1÷(-23)=1÷(-8)=-18,不正确;
④(-10)-4÷(-10-1)-4=10-4÷104=10-8,不正确.故选B.
?
B
例题解读
例3 已知(2x+3)x+2 021=1,求x的值.
解:此题要分情况讨论.
①当2x+3=1时,解得x=-1,则x+2 021=2 020,
此时(2x+3)x+2 021=12 020=1.
②当2x+3=-1时,解得x=-2,则x+2 021=2 019,
此时(2x+3)x+2 021=(-1)2 019=-1.
③当x+2 021=0时,解得x=-2 021,则2x+3=2×(-2 021)+3=-4 039≠0,
此时(2x+3)x+2 021=(2x+3)0=1.
综上所述,x的值为-2 021或-1.
不要漏掉底数等于-1的情况,此时要求指数是偶数.
随堂练习
1.在-12,(x-3.14)0,2-1,0这四个数中,最小的数是( )
A.-12 B.(x-3.14)0 C.2-1 D.0
2.计算(12)-1-(-3)2的结果是 .
?
解析:-12=-1,(x-3.14)0=1,2-1=12,所以最小的数是-1,即-1?.故选A.
?
A
解析:(12)-1-(-3)2=2?9=?7.
?
-7
3. 计算下列各式:
随堂练习
课时小结
零次幂与负整数次幂
规定:a0=1(a≠0);a-p=1????p(a≠0,p是正整数).
即任何一个不等于零的数,它的零次幂等于1,
它的-p(p是正整数)次幂等于这个数的p次幂的倒数.
?
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.3 同底数幂的除法
第3课时 用科学记数法表示绝对值小于1的数
学习目标
1.会用科学记数法表示绝对值小于1的数.(重点)
2.借助自己熟悉的事物感受绝对值较小的数据.
知识回顾
1.用科学记数法表示绝对值较大的数
2.将用科学记数法表示的数还原的方法
一般地,一个绝对值大于10的数都可记成±a×10n的形式,其中1≤a<10,n是正整数,n 等于原数的整数位数减 1.
把一个用科学记数法表示的数还原时,只需将小数点向右移动 n 位(不足的数位用 0 补齐),并把乘号和10n 去掉即可.
情境导入
生活中的较小的数
①细胞的直径只有1微米(um),即0.000 001m.
②某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s.
③一个氧原子的质量0.000 000 000 000 000 000 000 000 026 57kg.
这些绝对值小于1的数如何表示呢?
新课讲授
用科学记数法表示绝对值小于1的数
不难得出
0.000 001=11?000?000=1106=1×10?6,
?
-0.000 43=?4.310?000=?4.3104=?4.3×10?4.
?
可见,绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零).
情境导入
0.000 000 000 000 000 000 000 000 026 57=2.657×10?26.
?
0.000 000 001=1109=1×10?9,
?
生活中的较小的数
①细胞的直径只有1微米(um),即0.000 001m.
②某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s.
③一个氧原子的质量0.000 000 000 000 000 000 000 000 026 57kg.
例 用科学记数法表示下列各数:
教材例题
0.000 76,
0.000 001 59.
0.000 76=7.6×0.000 1=7.6×10-4.
0.000 001 59=-1.59×0.000 001=-1.59×10-6.
例题解读
例1 用科学记数法表示下列各数:
(1)0.000 030 4;
(2)-0.000 000 305;
(3)2万5千亿;
(4)零点零零零四二.
解:(1)0.000 030 4=3.04×10-5;
(2)-0.000 000 305=-3.05×10-7;
(3)2万5千亿写作2 500 000 000 000,
2 500 000 000 000=2.5×1012;
(4)零点零零零四二写作0.000 42,
0.000 42=4.2×10-4.
例题解读
例2 用小数表示下列各数:
(1)2×10-7;
(2)3.14×10-5;
(3)7.08×10-3;
(4)2.17×10-2.
解:(1)2×10-7=0.000 000 2.
(2)3.14×10-5=0.000 031 4.
(3)7.08×10-3=0.007 08.
(4)2.17×10-2=0.021 7.
将科学记数法表示的数a×10-n“还原”成通常表示的数,
就是把a的小数点向左移动n位所得到的数.
例题解读
例3 在电子显微镜下测得一个圆球形体细胞的直径是0.000 005 cm,求20 000个这样的细胞排成的细胞链的长度.
解:0.000 005=5×10-6,20 000=2×104.
0.000 005×20 000=5×10-6×2×104
=5×2×10-6×104
=10×10-2=10-1
=0.1(cm).
答:20 000个这样的细胞排成的细胞链的长度为0.1 cm.
用科学记数法表示较大或较小的数,有利于按幂的运算性质简化计算.
随堂练习
1.用科学记数法表示下列各数.
(1)0.000 326 7; (2)-0.001 1;
(3)0.024 5;
(4)-0.000 010 42;
(5)0.002 001.
解:(1)0.000 326 7=3.267×10-4;
(2)-0.001 1=-1.1×10-3;
(3)0.024 5=2.45×10-2;
(4)-0.000 010 42=1.042×10-5;
(5)0.002 001=2.001×10-3.
随堂练习
2.写出原来的数,并指出精确到哪一位.
(1)-1×10-2; (2)-7.001×10-3;
(3)5.2×10-5;
(4)1.05×10-5.
解:(1)-1×10-2=-0.01,精确到百分位;
(2)-7.001×10-3=-0.007 001,精确到百万分位;
(3)5.2×10-5=0.000 052,精确到百万分位;
(4)1.05×10-5=0.000 010 5,精确到千万分位.
随堂练习
3.世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂,体长仅0.021厘米,其质量也只有0.000 005克.
(1)用科学记数法表示上述两个数据.
解:(1)0.021厘米用科学记数法表示为2.1×10-2厘米;
0.000 005克用科学记数法表示为5×10-6克.
随堂练习
3.世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂,体长仅0.021厘米,其质量也只有0.000 005克.
(1)用科学记数法表示上述两个数据.
(2)一个鸡蛋的质量大约是50克,多少只卵蜂的质量和与这个鸡蛋的质量相等?
(2)设x只卵蜂的质量和与这个鸡蛋的质量相等,
根据题意,得 0.000 005x=50,解得x=10 000 000=1×107.
所以1×107只卵蜂的质量和与这个鸡蛋的质量相等.
纳米
资
料
拓
展
课时小结
用科学记数法表示绝对值小于1的数
绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,
n是正整数,n等于原数中第一个不等于零的数字前面的零
的个数(包括小数点前面的一个零).
8.1 幂的运算
8.1.3 同底数幂的除法
第2课时 零次幂与负整数次幂
学习目标
1.理解零次幂和负整数指数幂的概念及性质.
2.会熟练进行零次幂和负整数指数幂的运算.(重点、难点)
知识回顾
幂同底数幂的除法法则:
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减.
当m≤n时,
还成立吗?
= a·a·…·a
(m-n)个a
am÷an=
=am-n
(a·a·…·a)
(a·a·…·a)
m个a
n个a
探 究
(1)当被除式的指数等于除式的指数(即m=n)时,例如,
33÷33=______,108÷108=______,an÷an=______.
1
1
1
容易看出所得的商都是1.
另一方面,仿照同底数幂的除法的性质进行计算,得
33÷33=33-3=30=1,
108÷108=103-3=100=1,
an÷an=an-n=a0=1.
出现零次幂。
约定:a0=1(a≠0).
任何一个不等于零的数的零次幂都等于1.
探 究
(2)当被除式的指数小于除式的指数(即m<n)时,例如,
32÷35=______,104÷108=______,am÷an=___________.
那么可以通过分数约分,得
32÷35=3?35=3?3?×3?=13?,
?
104÷108=104108=104104×104=1104,
?
am÷an=????????????????=1?????????
探 究
(2)当被除式的指数小于除式的指数(即m<n)时,例如,
32÷35=______,104÷108=______,am÷an=______________.
另一方面,仿照同底数幂的除法的性质进行计算,得
32÷35=32-5=3-3,104÷108=104-8=10-4,
am÷an=am-n=a-p.(p=n-m)
3-3 10-4 a-p(p=n-m)
出现负整数次幂。
约定:a-p=????????????(a≠0,p是正整数).任何一个不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数.
?
幂同底数幂的除法法则:
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
归纳总结
当m≤n时,也成立.
规定:a0=1(a≠0);a-p=1????p(a≠0,p是正整数).
即任何一个不等于零的数,它的零次幂等于1,
它的-p(p是正整数)次幂等于这个数的p次幂的倒数.
?
教材例题
例 计算:
(1)106÷106; (2)(17)0÷(17)-2; (3)(-2)3÷(-2)5.
?
解:(1)106÷106=106?6=100=1.
?
(2)(17)0÷(17)?2=(17)0?(?2)=(17)2=149.
?
(3)(-2)3÷(-2)5=(?2)3?5=(?2)?2=1(?2)?=14.
?
例题解读
例1 用小数或分数表示下列各数:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
解:(1)10-3=110?=11?000=0.001.
?
(2)70×8-2=1×18?=164.
?
(3)1.6×10-4=1.6×1104=1.6×0.000?1=0.000?16.
?
例题解读
例2 下列各式的计算中,不正确的个数是( )
①100÷10-1=10; ②10-4×(2×7)0=10 000;
③(-0.1)0÷(-2-1)-3=8; ④(-10)-4÷(-10-1)-4=-1.
A.4 B.3 C.2 D.1
解析:①100÷10-1=1÷110=10,正确;
②10-4×(2×7)0=1104×1=0.000 1,不正确;
③(-0.1)0÷(-2-1)-3=1÷(-23)=1÷(-8)=-18,不正确;
④(-10)-4÷(-10-1)-4=10-4÷104=10-8,不正确.故选B.
?
B
例题解读
例3 已知(2x+3)x+2 021=1,求x的值.
解:此题要分情况讨论.
①当2x+3=1时,解得x=-1,则x+2 021=2 020,
此时(2x+3)x+2 021=12 020=1.
②当2x+3=-1时,解得x=-2,则x+2 021=2 019,
此时(2x+3)x+2 021=(-1)2 019=-1.
③当x+2 021=0时,解得x=-2 021,则2x+3=2×(-2 021)+3=-4 039≠0,
此时(2x+3)x+2 021=(2x+3)0=1.
综上所述,x的值为-2 021或-1.
不要漏掉底数等于-1的情况,此时要求指数是偶数.
随堂练习
1.在-12,(x-3.14)0,2-1,0这四个数中,最小的数是( )
A.-12 B.(x-3.14)0 C.2-1 D.0
2.计算(12)-1-(-3)2的结果是 .
?
解析:-12=-1,(x-3.14)0=1,2-1=12,所以最小的数是-1,即-1?.故选A.
?
A
解析:(12)-1-(-3)2=2?9=?7.
?
-7
3. 计算下列各式:
随堂练习
课时小结
零次幂与负整数次幂
规定:a0=1(a≠0);a-p=1????p(a≠0,p是正整数).
即任何一个不等于零的数,它的零次幂等于1,
它的-p(p是正整数)次幂等于这个数的p次幂的倒数.
?
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.3 同底数幂的除法
第3课时 用科学记数法表示绝对值小于1的数
学习目标
1.会用科学记数法表示绝对值小于1的数.(重点)
2.借助自己熟悉的事物感受绝对值较小的数据.
知识回顾
1.用科学记数法表示绝对值较大的数
2.将用科学记数法表示的数还原的方法
一般地,一个绝对值大于10的数都可记成±a×10n的形式,其中1≤a<10,n是正整数,n 等于原数的整数位数减 1.
把一个用科学记数法表示的数还原时,只需将小数点向右移动 n 位(不足的数位用 0 补齐),并把乘号和10n 去掉即可.
情境导入
生活中的较小的数
①细胞的直径只有1微米(um),即0.000 001m.
②某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s.
③一个氧原子的质量0.000 000 000 000 000 000 000 000 026 57kg.
这些绝对值小于1的数如何表示呢?
新课讲授
用科学记数法表示绝对值小于1的数
不难得出
0.000 001=11?000?000=1106=1×10?6,
?
-0.000 43=?4.310?000=?4.3104=?4.3×10?4.
?
可见,绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零).
情境导入
0.000 000 000 000 000 000 000 000 026 57=2.657×10?26.
?
0.000 000 001=1109=1×10?9,
?
生活中的较小的数
①细胞的直径只有1微米(um),即0.000 001m.
②某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000 000 001s.
③一个氧原子的质量0.000 000 000 000 000 000 000 000 026 57kg.
例 用科学记数法表示下列各数:
教材例题
0.000 76,
0.000 001 59.
0.000 76=7.6×0.000 1=7.6×10-4.
0.000 001 59=-1.59×0.000 001=-1.59×10-6.
例题解读
例1 用科学记数法表示下列各数:
(1)0.000 030 4;
(2)-0.000 000 305;
(3)2万5千亿;
(4)零点零零零四二.
解:(1)0.000 030 4=3.04×10-5;
(2)-0.000 000 305=-3.05×10-7;
(3)2万5千亿写作2 500 000 000 000,
2 500 000 000 000=2.5×1012;
(4)零点零零零四二写作0.000 42,
0.000 42=4.2×10-4.
例题解读
例2 用小数表示下列各数:
(1)2×10-7;
(2)3.14×10-5;
(3)7.08×10-3;
(4)2.17×10-2.
解:(1)2×10-7=0.000 000 2.
(2)3.14×10-5=0.000 031 4.
(3)7.08×10-3=0.007 08.
(4)2.17×10-2=0.021 7.
将科学记数法表示的数a×10-n“还原”成通常表示的数,
就是把a的小数点向左移动n位所得到的数.
例题解读
例3 在电子显微镜下测得一个圆球形体细胞的直径是0.000 005 cm,求20 000个这样的细胞排成的细胞链的长度.
解:0.000 005=5×10-6,20 000=2×104.
0.000 005×20 000=5×10-6×2×104
=5×2×10-6×104
=10×10-2=10-1
=0.1(cm).
答:20 000个这样的细胞排成的细胞链的长度为0.1 cm.
用科学记数法表示较大或较小的数,有利于按幂的运算性质简化计算.
随堂练习
1.用科学记数法表示下列各数.
(1)0.000 326 7; (2)-0.001 1;
(3)0.024 5;
(4)-0.000 010 42;
(5)0.002 001.
解:(1)0.000 326 7=3.267×10-4;
(2)-0.001 1=-1.1×10-3;
(3)0.024 5=2.45×10-2;
(4)-0.000 010 42=1.042×10-5;
(5)0.002 001=2.001×10-3.
随堂练习
2.写出原来的数,并指出精确到哪一位.
(1)-1×10-2; (2)-7.001×10-3;
(3)5.2×10-5;
(4)1.05×10-5.
解:(1)-1×10-2=-0.01,精确到百分位;
(2)-7.001×10-3=-0.007 001,精确到百万分位;
(3)5.2×10-5=0.000 052,精确到百万分位;
(4)1.05×10-5=0.000 010 5,精确到千万分位.
随堂练习
3.世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂,体长仅0.021厘米,其质量也只有0.000 005克.
(1)用科学记数法表示上述两个数据.
解:(1)0.021厘米用科学记数法表示为2.1×10-2厘米;
0.000 005克用科学记数法表示为5×10-6克.
随堂练习
3.世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂,体长仅0.021厘米,其质量也只有0.000 005克.
(1)用科学记数法表示上述两个数据.
(2)一个鸡蛋的质量大约是50克,多少只卵蜂的质量和与这个鸡蛋的质量相等?
(2)设x只卵蜂的质量和与这个鸡蛋的质量相等,
根据题意,得 0.000 005x=50,解得x=10 000 000=1×107.
所以1×107只卵蜂的质量和与这个鸡蛋的质量相等.
纳米
资
料
拓
展
课时小结
用科学记数法表示绝对值小于1的数
绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,
n是正整数,n等于原数中第一个不等于零的数字前面的零
的个数(包括小数点前面的一个零).
