8.2.2(1) 整式乘法-----单项式与多项式相乘 课件 (共18张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.2.2(1) 整式乘法-----单项式与多项式相乘 课件 (共18张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 21:08:12 | ||
图片预览




文档简介
(共18张PPT)
第八章 整式乘法与因式分解
8.2 整式乘法
8.2.2 单项式与多项式相乘
第1课时 单项式乘多项式
学习目标
1.能根据乘法分配律和单项式与单项式相乘的法则探究单项式与多项式相乘的法则.(重点、难点)
2.掌握单项式与多项式相乘的法则,并会利用法则进行乘法运算.(重点)
知识回顾
1. 同底数幂相乘,底数不变,指数相加.
2. 幂的乘方,底数不变,指数相乘
(am)n=amn(m,n为正整数)
am·an=am+n(m,n为正整数)
3. 积的乘方等于各因数乘方的积.
(ab)n=anbn(n为正整数)
知识回顾
单项式的乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
情境导入
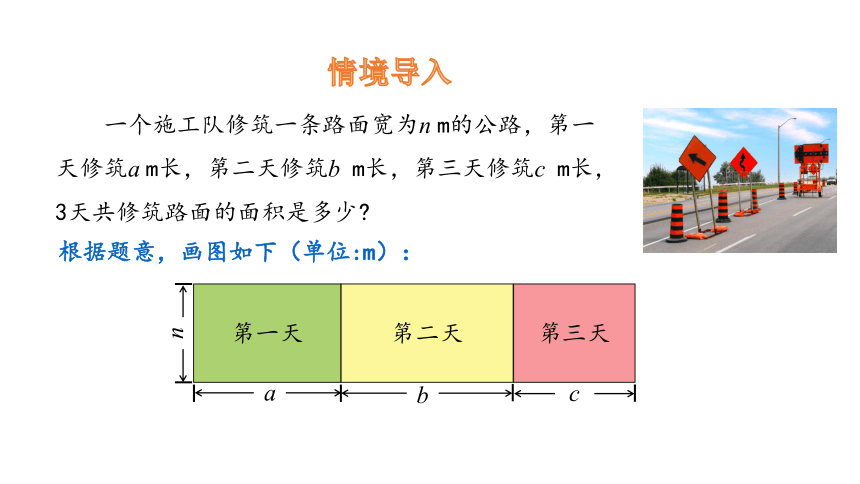
一个施工队修筑一条路面宽为n m的公路,第一天修筑a m长,第二天修筑b m长,第三天修筑c m长,3天共修筑路面的面积是多少
根据题意,画图如下(单位:m):
第一天
第二天
第三天
n
a
b
c
情境导入
第一天
第二天
第三天
n
a
b
c
a+b+c
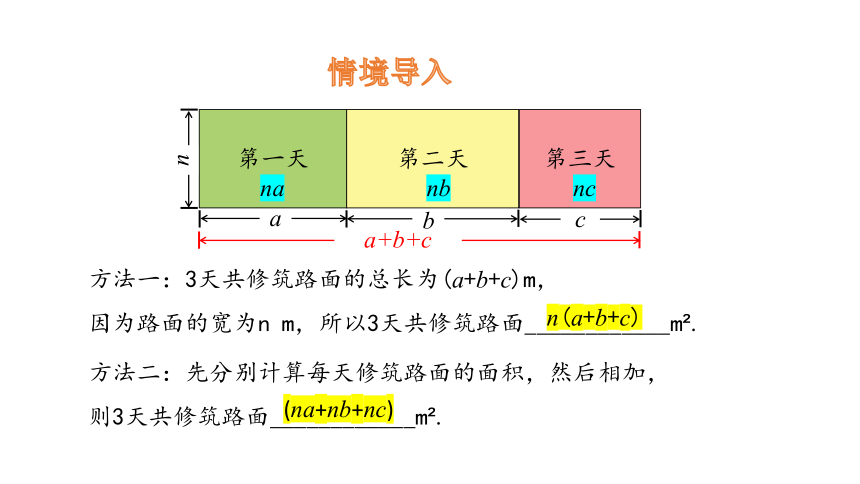
方法一:3天共修筑路面的总长为(a+b+c)m,
因为路面的宽为n m,所以3天共修筑路面____________m .
n(a+b+c)
方法二:先分别计算每天修筑路面的面积,然后相加,
则3天共修筑路面____________m .
na
nb
nc
(na+nb+nc)
情境导入
第一天
第二天
第三天
n
a
b
c
a+b+c
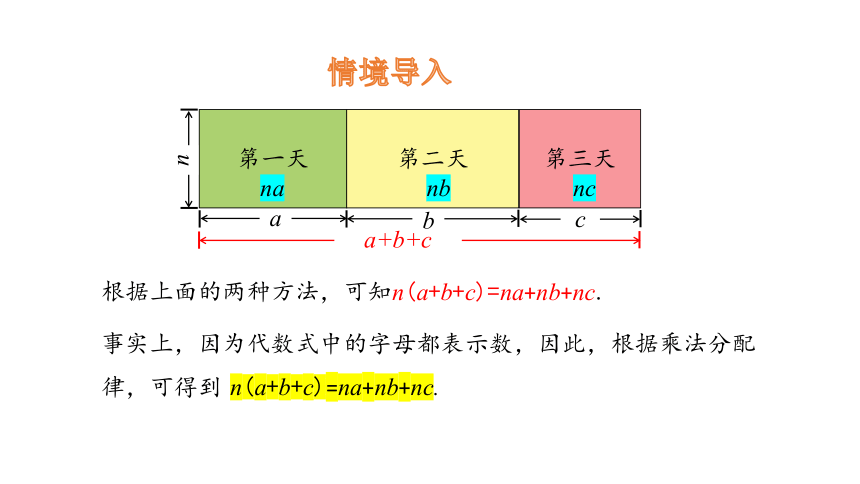
根据上面的两种方法,可知n(a+b+c)=na+nb+nc.
事实上,因为代数式中的字母都表示数,因此,根据乘法分配律,可得到
na
nb
nc
n(a+b+c)=na+nb+nc.
知识要点
单项式与多项式的乘法法则:
注意:单项式乘多项式的每一项时,要注意各项符号的确定.
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
教材例题
例 计算:
(1)(-2x)(x2-x+1); (2)a(a2+a)-a2(a-2).
解:(1)(-2x)(x2-x+1)
=(-2x)x2+(-2x)·(-x)+(-2x)·1
=-2x3+2x2-2x.
(2)a(a2+a)-a2(a-2)
=a·a2+a·a-a2·a+2a2
=a3+a2-a3+2a2
=3a2.
例题解读
例1 计算:
(1)2ab(5ab2+3a2b);
(2)(ab -2ab)·ab;
(3)-5m2n(2n+3m-n2);
(4)2(x+y2z+xy2z3)·xyz.
原式=2ab·5ab2+2ab·3a2b
=10a b +6a b .
原式=-5m2n·2n-5m2n·3m-
5m2n·(-n2)
=-10m2n -15m n+5m n .
原式=(2x+2y2z+2xy2z3)·xyz
=2x·xyz+2y2z·xyz+2xy2z3·xyz
=2x yz+2xy z +2x y z4.
原式=ab ·ab+(-2ab)·ab
=a b -a b .
例题解读
例2 镇纸是中国古代传统工艺品,是指写字作画时用以压纸的东西,也称作镇尺、压尺. 某长方体形状的镇纸长为3a-4,宽为2a,高为2a,求它的体积.
分析:长方体的体积公式为长×宽×高,代入式子,根据单项式乘多项式的运算法则计算即可.
解:它的体积为(3a-4)·2a·2a
=3a·2a·2a-4×2a·2a
=12a -16a .
例题解读
例3.
解析:根据题意,得
原式=9mn·(8m+5n)
=72m2n+45mn2.
故选B.
B
例题解读
例4 先化简,再求值:
5a(2a2-5a+3)-2a2(5a+5)+7a2,其中 a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a,
当 a=2 时,原式=-82.
方法总结:在计算时要注意先化简然后再代值计算.
整式的加减运算实际上就是去括号与合并同类项.
随堂练习
1.(2020兰州中考)化简:a(a-2)+4a=( )
A.a2+2a B.a2+6a C.a2-6a D.a2+4a-2
A
2.(济宁金乡期末)在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:-3x(-2x2+3x-1)=6x3-9x2+□.“□”的地方被墨水弄污了,你认为“□”内应填写( )
A. 1 B. -1 C. 3x D. -3x
C
随堂练习
3
随堂练习
4.如图,梯形ABCD的下底长为a,上底长为b,四边形ABEF是正方形.用多项式表示图中阴影部分的面积.
分析:图中阴影部分的面积=梯形ABCD的面积-空白正方形ABEF的面积.
根据图可知,正方形ABEF的边长为b.
随堂练习
5.先化简,再求值.
3a(2a2 - 4a + 3) - 2a2(3a + 4),其中 a = -2.
解:3a(2a2 - 4a + 3) - 2a2(3a + 4)
= 6a3 - 12a2 + 9a - 6a3 - 8a2
= -20a2 + 9a.
当 a = -2 时,原式 = -20×(-2)2 + 9×(-2) = -98.
课时小结
单项式与多项式的乘法法则
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
单项式与多项式相乘注意三点
(1)先算乘方,再算乘法,最后算加减;
(2)计算的结果仍是多项式,结果中有同类项的要合并同类项;
(3)积的符号由单项式的符号与多项式项的符号确定.
第八章 整式乘法与因式分解
8.2 整式乘法
8.2.2 单项式与多项式相乘
第1课时 单项式乘多项式
学习目标
1.能根据乘法分配律和单项式与单项式相乘的法则探究单项式与多项式相乘的法则.(重点、难点)
2.掌握单项式与多项式相乘的法则,并会利用法则进行乘法运算.(重点)
知识回顾
1. 同底数幂相乘,底数不变,指数相加.
2. 幂的乘方,底数不变,指数相乘
(am)n=amn(m,n为正整数)
am·an=am+n(m,n为正整数)
3. 积的乘方等于各因数乘方的积.
(ab)n=anbn(n为正整数)
知识回顾
单项式的乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
情境导入
一个施工队修筑一条路面宽为n m的公路,第一天修筑a m长,第二天修筑b m长,第三天修筑c m长,3天共修筑路面的面积是多少
根据题意,画图如下(单位:m):
第一天
第二天
第三天
n
a
b
c
情境导入
第一天
第二天
第三天
n
a
b
c
a+b+c
方法一:3天共修筑路面的总长为(a+b+c)m,
因为路面的宽为n m,所以3天共修筑路面____________m .
n(a+b+c)
方法二:先分别计算每天修筑路面的面积,然后相加,
则3天共修筑路面____________m .
na
nb
nc
(na+nb+nc)
情境导入
第一天
第二天
第三天
n
a
b
c
a+b+c
根据上面的两种方法,可知n(a+b+c)=na+nb+nc.
事实上,因为代数式中的字母都表示数,因此,根据乘法分配律,可得到
na
nb
nc
n(a+b+c)=na+nb+nc.
知识要点
单项式与多项式的乘法法则:
注意:单项式乘多项式的每一项时,要注意各项符号的确定.
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
教材例题
例 计算:
(1)(-2x)(x2-x+1); (2)a(a2+a)-a2(a-2).
解:(1)(-2x)(x2-x+1)
=(-2x)x2+(-2x)·(-x)+(-2x)·1
=-2x3+2x2-2x.
(2)a(a2+a)-a2(a-2)
=a·a2+a·a-a2·a+2a2
=a3+a2-a3+2a2
=3a2.
例题解读
例1 计算:
(1)2ab(5ab2+3a2b);
(2)(ab -2ab)·ab;
(3)-5m2n(2n+3m-n2);
(4)2(x+y2z+xy2z3)·xyz.
原式=2ab·5ab2+2ab·3a2b
=10a b +6a b .
原式=-5m2n·2n-5m2n·3m-
5m2n·(-n2)
=-10m2n -15m n+5m n .
原式=(2x+2y2z+2xy2z3)·xyz
=2x·xyz+2y2z·xyz+2xy2z3·xyz
=2x yz+2xy z +2x y z4.
原式=ab ·ab+(-2ab)·ab
=a b -a b .
例题解读
例2 镇纸是中国古代传统工艺品,是指写字作画时用以压纸的东西,也称作镇尺、压尺. 某长方体形状的镇纸长为3a-4,宽为2a,高为2a,求它的体积.
分析:长方体的体积公式为长×宽×高,代入式子,根据单项式乘多项式的运算法则计算即可.
解:它的体积为(3a-4)·2a·2a
=3a·2a·2a-4×2a·2a
=12a -16a .
例题解读
例3.
解析:根据题意,得
原式=9mn·(8m+5n)
=72m2n+45mn2.
故选B.
B
例题解读
例4 先化简,再求值:
5a(2a2-5a+3)-2a2(5a+5)+7a2,其中 a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a,
当 a=2 时,原式=-82.
方法总结:在计算时要注意先化简然后再代值计算.
整式的加减运算实际上就是去括号与合并同类项.
随堂练习
1.(2020兰州中考)化简:a(a-2)+4a=( )
A.a2+2a B.a2+6a C.a2-6a D.a2+4a-2
A
2.(济宁金乡期末)在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:-3x(-2x2+3x-1)=6x3-9x2+□.“□”的地方被墨水弄污了,你认为“□”内应填写( )
A. 1 B. -1 C. 3x D. -3x
C
随堂练习
3
随堂练习
4.如图,梯形ABCD的下底长为a,上底长为b,四边形ABEF是正方形.用多项式表示图中阴影部分的面积.
分析:图中阴影部分的面积=梯形ABCD的面积-空白正方形ABEF的面积.
根据图可知,正方形ABEF的边长为b.
随堂练习
5.先化简,再求值.
3a(2a2 - 4a + 3) - 2a2(3a + 4),其中 a = -2.
解:3a(2a2 - 4a + 3) - 2a2(3a + 4)
= 6a3 - 12a2 + 9a - 6a3 - 8a2
= -20a2 + 9a.
当 a = -2 时,原式 = -20×(-2)2 + 9×(-2) = -98.
课时小结
单项式与多项式的乘法法则
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
单项式与多项式相乘注意三点
(1)先算乘方,再算乘法,最后算加减;
(2)计算的结果仍是多项式,结果中有同类项的要合并同类项;
(3)积的符号由单项式的符号与多项式项的符号确定.
