8.3(1) 完全平方公式与平方差公式-----完全平方公式 课件 (共20张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.3(1) 完全平方公式与平方差公式-----完全平方公式 课件 (共20张PPT) 2023-2024学年数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 227.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第八章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
8.3.1 完全平方公式
学习目标
1.能根据多项式的乘法推导出完全平方公式.(重点)
2.理解并掌握完全平方公式,并能进行计算.(重点、难点)
知识回顾
(1)a 表示的意义是:
(2)(a+b) 表示的意义是:
a 表示两个a相乘.
(a+b) 表示两个(a+b)相乘.
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
多项式与多项式的乘法法则
新课引入
观察下列算式及其运算结果,你发现了什么规律
发现:两数和的平方,等于它们的平方和加上它们的积的2倍.
6m=2×m×3
(2+3x)2=(2+3x)(2+3x)
=22+2×3x+2×3x+9x2
=4+12x+9x .
(m+3)2=(m+3)(m+3)
=m2+3m+3m+9
=m2+6m+9;
12x=2×2×3x
新课讲授
完全平方公式用语言叙述是:两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
由多项式乘法可得乘法公式
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
左侧两个公式,可以直接应用于运算,称为完全平方公式.
新课讲授
由多项式乘法可得乘法公式
请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式.
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
另外,在公式(a+b) =a +2ab+b 中用-b代替b,
可得[a+(-b)] =a +2a·(-b)+(-b) ,
即(a-b) =a -2ab+b .
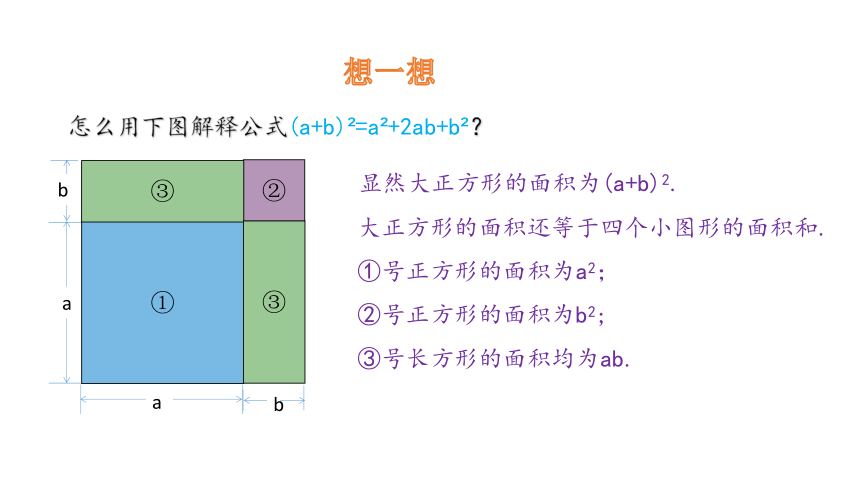
想一想
怎么用下图解释公式(a+b) =a +2ab+b ?
a
a
b
b
①
②
③
③
显然大正方形的面积为(a+b)2.
大正方形的面积还等于四个小图形的面积和.
①号正方形的面积为a2;
②号正方形的面积为b2;
③号长方形的面积均为ab.
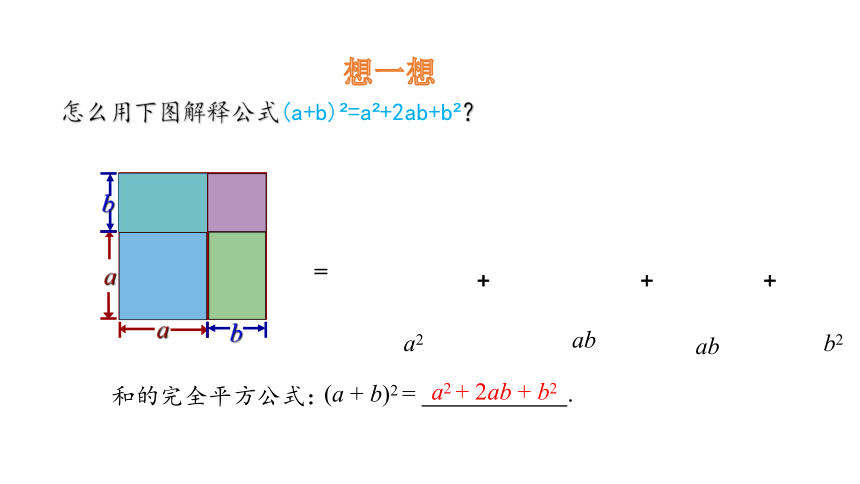
想一想
怎么用下图解释公式(a+b) =a +2ab+b ?
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a + b)2 = .
a2 + 2ab + b2
和的完全平方公式:
图中大正方形的面积为a2;
图中两个绿色长方形的面积均为ab;
图中蓝色正方形的面积为b2;
因此红色正方形的面积=大正方形的面积-2个绿色长方形的面积+蓝色正方形的面积,即(a-b) =a -2ab+b .
怎么用下图解释公式(a-b) =a -2ab+b ?
图中红色正方形的面积为(a-b)2;
想一想
教材例题
例 利用乘法公式计算:
(1)(2x+y) ; (2)(3a-2b) .
解:运用公式计算,要先识别a,b在具体式子中分别表示什么.
(1)(2x+y) =(2x) +2·(2x)y+y
=4x +4xy+y .
(a + b) = a + 2 a b + b
(2)(3a-2b) =(3a) +2·(3a)(2b)+(2b)
=9a -12ab+4b .
(a - b) = a - 2 a b + b
例题解读
例1 用完全平方公式计算:
(1)(2x-3)2; (2)(4x+5y)2; (3)(m-a) .
解:(1)(2x-3)(2x-3)
=4x -6x-6x+9
=4x -12x+9.
(2)(4x+5y)(4x+5y)
=16x +20xy+20xy+25y
=16x +40xy+25y .
(3)()()
=
= .
例题解读
例2.若x2+(m-3)x+16是完全平方式,则m的值为( )
A.11或-7 B.13或-7 C.11或-5 D.13或-5
解析:x2+(m-3)x+16可以写成x2+(m-3)x+4 或x2+(m-3)x+(-4) 的形式.
若x2+(m-3)x+4 是完全平方式,
则(m-3)x=2×x×4=8x,所以m=11;
若x2+(m-3)x+(-4) 是完全平方式,
则(m-3)x=2×x×(-4)=-8x,所以m=-5.
因此,m的值可能为11或-5.
C
例题解读
例3.一个正方形的边长增加3 cm,它的面积就增加99 cm2,这个正方形的边长为 .
解析:不妨设这个正方形的边长为x cm,
则增加3 cm后边长为(x+3)cm,
所以正方形的面积增加99 cm ,
可列方程为(x+3) -x =99.
从而解得x=15.
15 cm
例题解读
例4.利用完全平方公式计算:
(1)1022; (2)1972.
(2)1972
=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809.
解:(1)1022
=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10 404.
例题解读
例5 计算:(x + y + z)2.
解:原式 = [x + (y + z)]2
= x2 + 2x(y + z) + (y + z)2
= x2 + 2xy + 2xz + y2 + 2yz + z2
= x2 + y2 + z2 + 2xy + 2xz + 2yz.
方法总结:运用分组和整体思想计算,该等式也称为三数的完全平方公式.
随堂练习
1. 下列变形中,错误的是( )
①(b-4c)2=b2-16c2; ②(a-2bc)2=a2+4abc+4b2c2;
③(x+y)2=x2+xy+y2; ④(4m-n)2=16m2-8mn+n2.
A.①②③ B.①②④
C.①③④ D.②③④
A
2.已知(a+b)2=49,a2+b2=25,则ab=( )
A.24 B.48 C.12 D.5
C
随堂练习
3.计算:
(1)(a-b)2;
(2)(2x-3y)2;
(3)(2x+y2)2;
(4)(x+3)2;
(5)(x-3)2;
(6)(2m-n)2;
(a-b) =a -ab-ba+b =a -2ab+b .
(2x-3y) =4x -6xy-6xy+9y =4x -12xy+9y .
(2x+y ) =4x +2xy +2xy +y4=4x +4y +y4.
(x+3) =x +3x+3x+9=x +6x+9.
(x-3) =x -3x-3x+9=x -6x+9.
(2m-n) =4m -2mn-2mn+n =4m -4mn+n .
随堂练习
4.(河北中考)现有甲、乙、丙三种不同的正方形和长方形纸片(边长如图).
(1)取甲、乙纸片各1块,其面积和为________;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片________块.
a2+b2
4
例题解读
5.用完全平方公式计算:
(1)205 ; (2)499 ; (3)46 .
原式=(200+5)
=200 +2×200×5+25
=40 000+2 000+25
=42 250.
原式=(500-1)
=500 -2×500×1+1
=250 000-1 000+1
=249001.
计算前观察原数是哪两个数的和或者差,然后再计算.
原式=(50-4)
=50 -2×50×4+16
=2 500-400+16
=2 416.
课时小结
1. 完全平方公式
两个数的和(或差)的平方,等于这个两个数的平方和加(或减)这两个数的乘积的2倍.用字母表示为:(a+b) =a +2ab+b ,(a-b) =a -2ab+b .
2. 完全平方公式的特点
(1)左边是一个二项式的完全平方.
(2)右边是一个二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍.
巧记:首平方,尾平方,积的2倍在中央.
第八章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
8.3.1 完全平方公式
学习目标
1.能根据多项式的乘法推导出完全平方公式.(重点)
2.理解并掌握完全平方公式,并能进行计算.(重点、难点)
知识回顾
(1)a 表示的意义是:
(2)(a+b) 表示的意义是:
a 表示两个a相乘.
(a+b) 表示两个(a+b)相乘.
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
多项式与多项式的乘法法则
新课引入
观察下列算式及其运算结果,你发现了什么规律
发现:两数和的平方,等于它们的平方和加上它们的积的2倍.
6m=2×m×3
(2+3x)2=(2+3x)(2+3x)
=22+2×3x+2×3x+9x2
=4+12x+9x .
(m+3)2=(m+3)(m+3)
=m2+3m+3m+9
=m2+6m+9;
12x=2×2×3x
新课讲授
完全平方公式用语言叙述是:两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
由多项式乘法可得乘法公式
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
左侧两个公式,可以直接应用于运算,称为完全平方公式.
新课讲授
由多项式乘法可得乘法公式
请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式.
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
另外,在公式(a+b) =a +2ab+b 中用-b代替b,
可得[a+(-b)] =a +2a·(-b)+(-b) ,
即(a-b) =a -2ab+b .
想一想
怎么用下图解释公式(a+b) =a +2ab+b ?
a
a
b
b
①
②
③
③
显然大正方形的面积为(a+b)2.
大正方形的面积还等于四个小图形的面积和.
①号正方形的面积为a2;
②号正方形的面积为b2;
③号长方形的面积均为ab.
想一想
怎么用下图解释公式(a+b) =a +2ab+b ?
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a + b)2 = .
a2 + 2ab + b2
和的完全平方公式:
图中大正方形的面积为a2;
图中两个绿色长方形的面积均为ab;
图中蓝色正方形的面积为b2;
因此红色正方形的面积=大正方形的面积-2个绿色长方形的面积+蓝色正方形的面积,即(a-b) =a -2ab+b .
怎么用下图解释公式(a-b) =a -2ab+b ?
图中红色正方形的面积为(a-b)2;
想一想
教材例题
例 利用乘法公式计算:
(1)(2x+y) ; (2)(3a-2b) .
解:运用公式计算,要先识别a,b在具体式子中分别表示什么.
(1)(2x+y) =(2x) +2·(2x)y+y
=4x +4xy+y .
(a + b) = a + 2 a b + b
(2)(3a-2b) =(3a) +2·(3a)(2b)+(2b)
=9a -12ab+4b .
(a - b) = a - 2 a b + b
例题解读
例1 用完全平方公式计算:
(1)(2x-3)2; (2)(4x+5y)2; (3)(m-a) .
解:(1)(2x-3)(2x-3)
=4x -6x-6x+9
=4x -12x+9.
(2)(4x+5y)(4x+5y)
=16x +20xy+20xy+25y
=16x +40xy+25y .
(3)()()
=
= .
例题解读
例2.若x2+(m-3)x+16是完全平方式,则m的值为( )
A.11或-7 B.13或-7 C.11或-5 D.13或-5
解析:x2+(m-3)x+16可以写成x2+(m-3)x+4 或x2+(m-3)x+(-4) 的形式.
若x2+(m-3)x+4 是完全平方式,
则(m-3)x=2×x×4=8x,所以m=11;
若x2+(m-3)x+(-4) 是完全平方式,
则(m-3)x=2×x×(-4)=-8x,所以m=-5.
因此,m的值可能为11或-5.
C
例题解读
例3.一个正方形的边长增加3 cm,它的面积就增加99 cm2,这个正方形的边长为 .
解析:不妨设这个正方形的边长为x cm,
则增加3 cm后边长为(x+3)cm,
所以正方形的面积增加99 cm ,
可列方程为(x+3) -x =99.
从而解得x=15.
15 cm
例题解读
例4.利用完全平方公式计算:
(1)1022; (2)1972.
(2)1972
=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809.
解:(1)1022
=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10 404.
例题解读
例5 计算:(x + y + z)2.
解:原式 = [x + (y + z)]2
= x2 + 2x(y + z) + (y + z)2
= x2 + 2xy + 2xz + y2 + 2yz + z2
= x2 + y2 + z2 + 2xy + 2xz + 2yz.
方法总结:运用分组和整体思想计算,该等式也称为三数的完全平方公式.
随堂练习
1. 下列变形中,错误的是( )
①(b-4c)2=b2-16c2; ②(a-2bc)2=a2+4abc+4b2c2;
③(x+y)2=x2+xy+y2; ④(4m-n)2=16m2-8mn+n2.
A.①②③ B.①②④
C.①③④ D.②③④
A
2.已知(a+b)2=49,a2+b2=25,则ab=( )
A.24 B.48 C.12 D.5
C
随堂练习
3.计算:
(1)(a-b)2;
(2)(2x-3y)2;
(3)(2x+y2)2;
(4)(x+3)2;
(5)(x-3)2;
(6)(2m-n)2;
(a-b) =a -ab-ba+b =a -2ab+b .
(2x-3y) =4x -6xy-6xy+9y =4x -12xy+9y .
(2x+y ) =4x +2xy +2xy +y4=4x +4y +y4.
(x+3) =x +3x+3x+9=x +6x+9.
(x-3) =x -3x-3x+9=x -6x+9.
(2m-n) =4m -2mn-2mn+n =4m -4mn+n .
随堂练习
4.(河北中考)现有甲、乙、丙三种不同的正方形和长方形纸片(边长如图).
(1)取甲、乙纸片各1块,其面积和为________;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片________块.
a2+b2
4
例题解读
5.用完全平方公式计算:
(1)205 ; (2)499 ; (3)46 .
原式=(200+5)
=200 +2×200×5+25
=40 000+2 000+25
=42 250.
原式=(500-1)
=500 -2×500×1+1
=250 000-1 000+1
=249001.
计算前观察原数是哪两个数的和或者差,然后再计算.
原式=(50-4)
=50 -2×50×4+16
=2 500-400+16
=2 416.
课时小结
1. 完全平方公式
两个数的和(或差)的平方,等于这个两个数的平方和加(或减)这两个数的乘积的2倍.用字母表示为:(a+b) =a +2ab+b ,(a-b) =a -2ab+b .
2. 完全平方公式的特点
(1)左边是一个二项式的完全平方.
(2)右边是一个二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍.
巧记:首平方,尾平方,积的2倍在中央.
