8.3(2) 完全平方公式与平方差公式-----平方差公式 课件 (共24张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.3(2) 完全平方公式与平方差公式-----平方差公式 课件 (共24张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 318.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 23:39:21 | ||
图片预览





文档简介
(共24张PPT)
第八章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
8.3.2 平方差公式
学习目标
1.掌握平方差公式的推导和运用,并理解平方差公式的几何背景.(重点)
2.掌握平方差公式的应用.(重点、难点)
知识回顾
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
1.多项式与多项式的乘法法则
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
2.完全平方公式
情境导入
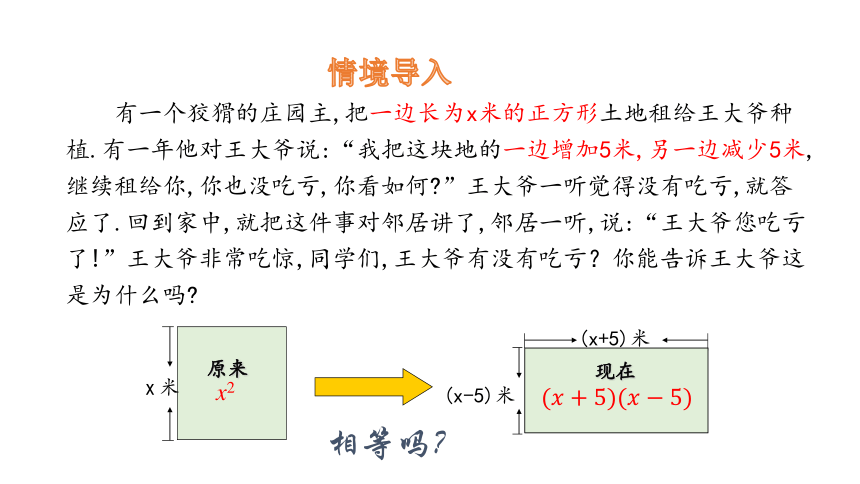
有一个狡猾的庄园主,把一边长为x米的正方形土地租给王大爷种植.有一年他对王大爷说:“我把这块地的一边增加5米,另一边减少5米,继续租给你,你也没吃亏,你看如何 ”王大爷一听觉得没有吃亏,就答应了.回到家中,就把这件事对邻居讲了,邻居一听,说:“王大爷您吃亏了!”王大爷非常吃惊,同学们,王大爷有没有吃亏?你能告诉王大爷这是为什么吗
x 米
原来
x2
(x-5)米
(x+5)米
现在
相等吗?
思 考
1.由多项式乘法计算:
(1)(3m+1)(3m-1); (2)(x +y)(x -y).
解:(1)(3m+1)(3m-1)
=3m·3m-3m+3m-1
=9m -1
(2)(x +y)(x -y)
=x ·x -x ·y+y·x -y·y
=x4-y2
2.你能得到(a+b)(a-b)的计算公式吗?
(a+b)(a-b)=a·a-a·b+b·a-b·b
=a2-b2
知识要点
(a+b)(a-b)=a -b .
这个公式称为平方差公式.
请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式.
用语言表述为:两数和与这两数差的积,等于它们的平方差.
知识要点
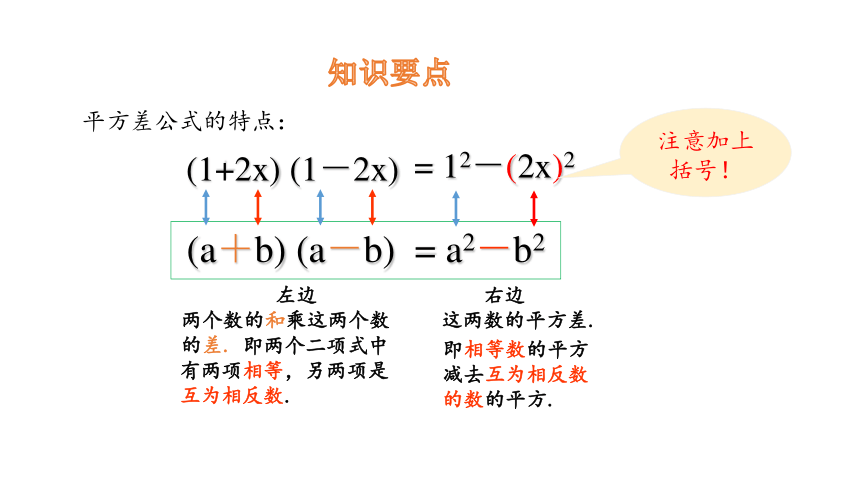
(a+b) (a-b) = a2-b2
左边
两个数的和乘这两个数
的差.
右边
这两数的平方差.
即两个二项式中有两项相等,另两项是互为相反数.
即相等数的平方
减去互为相反数
的数的平方.
(1+2x) (1-2x)
= 12-(2x)2
注意加上括号!
平方差公式的特点:
思 考
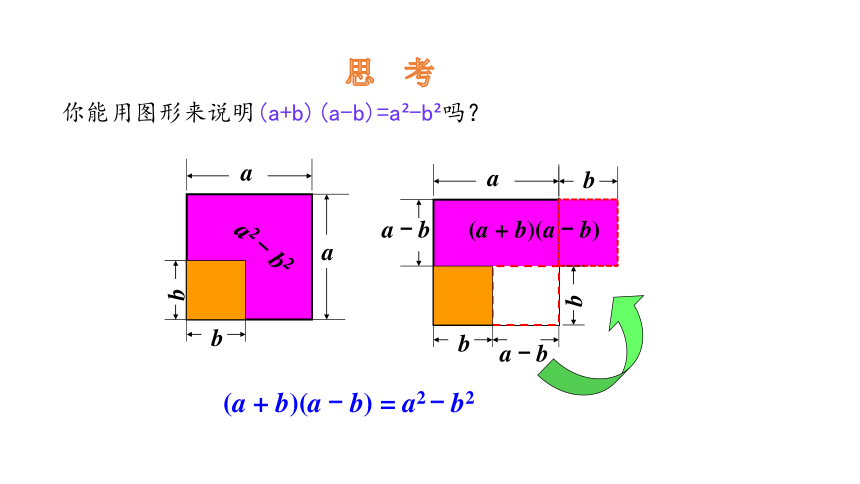
你能用图形来说明(a+b)(a-b)=a -b 吗?
a
a
b
b
a2 - b2
a
b
b
b
(a + b)(a - b)
(a + b)(a - b) = a2 - b2
a - b
a - b
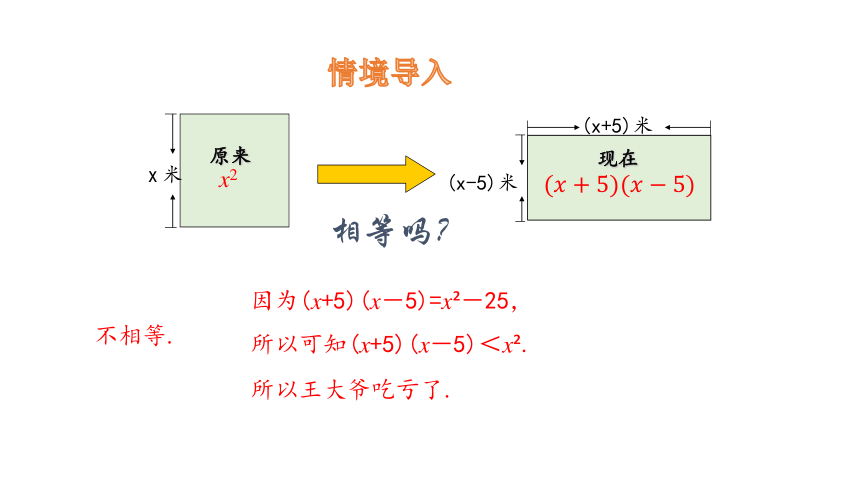
情境导入
x 米
原来
x2
(x-5)米
(x+5)米
现在
相等吗?
不相等.
因为(x+5)(x-5)=x -25,
所以可知(x+5)(x-5)<x .
所以王大爷吃亏了.
教材例题
例1 利用乘法公式计算:
(1)1 999×2 001; (2)(x+3)(x-3)(x +9).
解:(1)1 999×2 001
=(2 000-1)×(2 000+1)
=2 0002-12
=3 999 999.
(2)(x+3)(x-3)(x +9)
=(x -9)(x +9)
=x4-81.
教材例题
例2 计算:
(1)(a+b+c) ; (2)(a-b) .
解:(a+b+c) = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc.
解:(a-b) = (a-b)(a-b)
= (a-b)( a2-2ab + b2)
= a -2a2b+ab2-a2b+2ab -b3
=a -3a2b+3ab -b3.
思 考
(a-b)(-a-b)等于什么?
解:(a-b)(-a-b)可以看做是[(-b)+a][(-b)-a],
这样就转化为可以运用平方差公式的形式.
所以(a-b)(-a-b)=[(-b)+a][(-b)-a]=(-b) -a =b -a .
例题解读
例1 利用平方差公式计算:
(1)(5+6x)(5-6x); (2)(x-2y)(x+2y); (3)(-m+n)(-m-n).
解:(1)(5+6x)(5-6x)
=25-30x+30x-36x
=25-36x .
(2)(x-2y)(x+2y)
=x +2xy-2xy-4y
=x -4y .
注意(3)中,在运用平方差公式时,要把(-m)要看作一个整体,不要漏掉“-”.
(3)(-m+n)(-m-n)
=m +mn-mn-n
=m -n .
(2)(3x+2y)(9x2+4y2)(3x-2y)
=(3x+2y)(3x-2y)(9x2+4y2)
=[(3x)2-(2y)2](9x2+4y2)
=(9x2-4y2)(9x2+4y2)
=(9x2)2-(4y2)2=81x4-16y4.
解:(1)()()(x2+1)
=[() -1](x2+1)
=(x2-1)(x2+1)
=(x2) -1=x4-1.
例题解读
例2 计算:
(1)()()(x2+1); (2)(3x+2y)(9x2+4y2)(3x-2y).
计算结果一定要算到最后,注意连续运用平方差公式.
例题解读
例3 用平方差公式进行计算:
(1)103×97 (2)118×122
解:原式=(100+3)(100-3)
=100 -3
=9 991.
解:原式=(120-2)(120+2)
=120 -2
=14 396.
计算前观察是否满足平方差公式的特点,运用公式计算.
随堂练习
1、判断下列各题能否用平方差公式(a+b)(a-b)=a2-b2计算?
(2)(2x-2y)(2x+2y)
(3)(-m+n)(-m+n)
(4)(a+2b)(2a-b)
(1)(20-5)(20+5)
(6)[(x+z)+2y ] [(x+z)-2y]
(5)(a+b)(-a-b)
能
能
不能
能
不能
不能
随堂练习
2.(x-1)(x+1)-(x +1)的值是( )
A.2x B.0 C.-2 D.-1
3.对于任意整数n,能整除代数式(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
C
C
随堂练习
4.利用平方差公式计算:
(1); (2);
=(-11y) -()
=121y -x .
随堂练习
(3)(x+y)(x2+y2)(x-y).
解:(x+y)(x2+y2)(x-y)
=(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4.
4.利用平方差公式计算:
5.计算:
(1)a (a+b)(a-b)+a b ; (2)(2x-5)(2x+5)-2x(2x-3).
解:原式=a (a -b )+a b
=a4-a b +a b
=a4.
解:原式=(2x) -25-(4x -6x)
=4x -25-4x +6x
=6x-25.
随堂练习
随堂练习
6.计算:
(1)88×92; (2)25×24;
解:(1)88×92
=(90-2)(90+2)
=902-22
=8 100-4
=8 096.
解:(2)25×24
=(25+)(25-)
=252-()2
=625-
=624.
解:(3a+2b)(6a-5b)(2b-3a)(5b+6a)
=[(3a+2b)(2b-3a)][(6a-5b)(5b+6a)]
=(4b2-9a2)(36a2-25b2)
=4×36a2b2-4×25b4-9×36a4+9×25a2b2
=369a2b2-324a4-100b4.
7.计算:
(3a+2b)(6a-5b)(2b-3a)(5b+6a).
随堂练习
课时小结
1.平方差公式:
(a+b)(a-b)=a -b
用语言表述为:两数和与这两数差的积,等于它们的平方差.
课时小结
2. 平方差公式的特点
(1)左边是两个二项式的积,在这两个二项式中有一项(a)完全相同,另一项(b和-b)互为相反数.
(2)右边是乘式中两项(a和b)的平方差(相同项的平方减去符号相反项的平方).
(3)公式中的a和b可以是单项式也可以是多项式.
第八章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
8.3.2 平方差公式
学习目标
1.掌握平方差公式的推导和运用,并理解平方差公式的几何背景.(重点)
2.掌握平方差公式的应用.(重点、难点)
知识回顾
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
1.多项式与多项式的乘法法则
(a+b) =a +2ab+b .
(a-b) =a -2ab+b .
2.完全平方公式
情境导入
有一个狡猾的庄园主,把一边长为x米的正方形土地租给王大爷种植.有一年他对王大爷说:“我把这块地的一边增加5米,另一边减少5米,继续租给你,你也没吃亏,你看如何 ”王大爷一听觉得没有吃亏,就答应了.回到家中,就把这件事对邻居讲了,邻居一听,说:“王大爷您吃亏了!”王大爷非常吃惊,同学们,王大爷有没有吃亏?你能告诉王大爷这是为什么吗
x 米
原来
x2
(x-5)米
(x+5)米
现在
相等吗?
思 考
1.由多项式乘法计算:
(1)(3m+1)(3m-1); (2)(x +y)(x -y).
解:(1)(3m+1)(3m-1)
=3m·3m-3m+3m-1
=9m -1
(2)(x +y)(x -y)
=x ·x -x ·y+y·x -y·y
=x4-y2
2.你能得到(a+b)(a-b)的计算公式吗?
(a+b)(a-b)=a·a-a·b+b·a-b·b
=a2-b2
知识要点
(a+b)(a-b)=a -b .
这个公式称为平方差公式.
请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式.
用语言表述为:两数和与这两数差的积,等于它们的平方差.
知识要点
(a+b) (a-b) = a2-b2
左边
两个数的和乘这两个数
的差.
右边
这两数的平方差.
即两个二项式中有两项相等,另两项是互为相反数.
即相等数的平方
减去互为相反数
的数的平方.
(1+2x) (1-2x)
= 12-(2x)2
注意加上括号!
平方差公式的特点:
思 考
你能用图形来说明(a+b)(a-b)=a -b 吗?
a
a
b
b
a2 - b2
a
b
b
b
(a + b)(a - b)
(a + b)(a - b) = a2 - b2
a - b
a - b
情境导入
x 米
原来
x2
(x-5)米
(x+5)米
现在
相等吗?
不相等.
因为(x+5)(x-5)=x -25,
所以可知(x+5)(x-5)<x .
所以王大爷吃亏了.
教材例题
例1 利用乘法公式计算:
(1)1 999×2 001; (2)(x+3)(x-3)(x +9).
解:(1)1 999×2 001
=(2 000-1)×(2 000+1)
=2 0002-12
=3 999 999.
(2)(x+3)(x-3)(x +9)
=(x -9)(x +9)
=x4-81.
教材例题
例2 计算:
(1)(a+b+c) ; (2)(a-b) .
解:(a+b+c) = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc.
解:(a-b) = (a-b)(a-b)
= (a-b)( a2-2ab + b2)
= a -2a2b+ab2-a2b+2ab -b3
=a -3a2b+3ab -b3.
思 考
(a-b)(-a-b)等于什么?
解:(a-b)(-a-b)可以看做是[(-b)+a][(-b)-a],
这样就转化为可以运用平方差公式的形式.
所以(a-b)(-a-b)=[(-b)+a][(-b)-a]=(-b) -a =b -a .
例题解读
例1 利用平方差公式计算:
(1)(5+6x)(5-6x); (2)(x-2y)(x+2y); (3)(-m+n)(-m-n).
解:(1)(5+6x)(5-6x)
=25-30x+30x-36x
=25-36x .
(2)(x-2y)(x+2y)
=x +2xy-2xy-4y
=x -4y .
注意(3)中,在运用平方差公式时,要把(-m)要看作一个整体,不要漏掉“-”.
(3)(-m+n)(-m-n)
=m +mn-mn-n
=m -n .
(2)(3x+2y)(9x2+4y2)(3x-2y)
=(3x+2y)(3x-2y)(9x2+4y2)
=[(3x)2-(2y)2](9x2+4y2)
=(9x2-4y2)(9x2+4y2)
=(9x2)2-(4y2)2=81x4-16y4.
解:(1)()()(x2+1)
=[() -1](x2+1)
=(x2-1)(x2+1)
=(x2) -1=x4-1.
例题解读
例2 计算:
(1)()()(x2+1); (2)(3x+2y)(9x2+4y2)(3x-2y).
计算结果一定要算到最后,注意连续运用平方差公式.
例题解读
例3 用平方差公式进行计算:
(1)103×97 (2)118×122
解:原式=(100+3)(100-3)
=100 -3
=9 991.
解:原式=(120-2)(120+2)
=120 -2
=14 396.
计算前观察是否满足平方差公式的特点,运用公式计算.
随堂练习
1、判断下列各题能否用平方差公式(a+b)(a-b)=a2-b2计算?
(2)(2x-2y)(2x+2y)
(3)(-m+n)(-m+n)
(4)(a+2b)(2a-b)
(1)(20-5)(20+5)
(6)[(x+z)+2y ] [(x+z)-2y]
(5)(a+b)(-a-b)
能
能
不能
能
不能
不能
随堂练习
2.(x-1)(x+1)-(x +1)的值是( )
A.2x B.0 C.-2 D.-1
3.对于任意整数n,能整除代数式(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
C
C
随堂练习
4.利用平方差公式计算:
(1); (2);
=(-11y) -()
=121y -x .
随堂练习
(3)(x+y)(x2+y2)(x-y).
解:(x+y)(x2+y2)(x-y)
=(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4.
4.利用平方差公式计算:
5.计算:
(1)a (a+b)(a-b)+a b ; (2)(2x-5)(2x+5)-2x(2x-3).
解:原式=a (a -b )+a b
=a4-a b +a b
=a4.
解:原式=(2x) -25-(4x -6x)
=4x -25-4x +6x
=6x-25.
随堂练习
随堂练习
6.计算:
(1)88×92; (2)25×24;
解:(1)88×92
=(90-2)(90+2)
=902-22
=8 100-4
=8 096.
解:(2)25×24
=(25+)(25-)
=252-()2
=625-
=624.
解:(3a+2b)(6a-5b)(2b-3a)(5b+6a)
=[(3a+2b)(2b-3a)][(6a-5b)(5b+6a)]
=(4b2-9a2)(36a2-25b2)
=4×36a2b2-4×25b4-9×36a4+9×25a2b2
=369a2b2-324a4-100b4.
7.计算:
(3a+2b)(6a-5b)(2b-3a)(5b+6a).
随堂练习
课时小结
1.平方差公式:
(a+b)(a-b)=a -b
用语言表述为:两数和与这两数差的积,等于它们的平方差.
课时小结
2. 平方差公式的特点
(1)左边是两个二项式的积,在这两个二项式中有一项(a)完全相同,另一项(b和-b)互为相反数.
(2)右边是乘式中两项(a和b)的平方差(相同项的平方减去符号相反项的平方).
(3)公式中的a和b可以是单项式也可以是多项式.
