8.1.2(1) 幂的运算-----幂的乘方与积的乘方 课件 (共17张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.1.2(1) 幂的运算-----幂的乘方与积的乘方 课件 (共17张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 21:06:22 | ||
图片预览





文档简介
(共17张PPT)
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.2 幂的乘方与积的乘方
第1课时 幂的乘方
学习目标
1.理解幂的运算性质2,并掌握幂的乘方的运算.(重点)
2.运用幂的乘方解决实际问题.(难点)
3.正确区分幂的乘方与同底数幂的乘法.(难点)
知识回顾
幂的意义:
a×a×···×a = an
n个
幂同底数幂的乘法:
am·an=am+n(m,n都是正整数)
=(a·a·…·a)(a·a·…·a)
m个
n个
=(a·a·…·a)
(m+n)个
= am+n.
am·an
知识回顾
正方体的体积比与棱长比的关系
乙正方体的棱长是 2 cm, 则乙正方体的体积 V乙= cm3 .
V甲是V乙的 倍.
8
125
即 53 倍.
甲正方体的棱长是乙正方体的 5 倍,则甲正方体的棱长为_____cm,
甲正方体的体积V甲= cm3.
1 000
10
正方体的体积比=棱长比的立方
情境导入
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星
地球
太阳
情境导入
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星的半径是地球的10倍,它的体积是地球的10 倍!
太阳的半径是地球的10 倍,它的体积是地球的(10 ) 倍!
那么,你知道(10 ) 等于多少吗
思 考
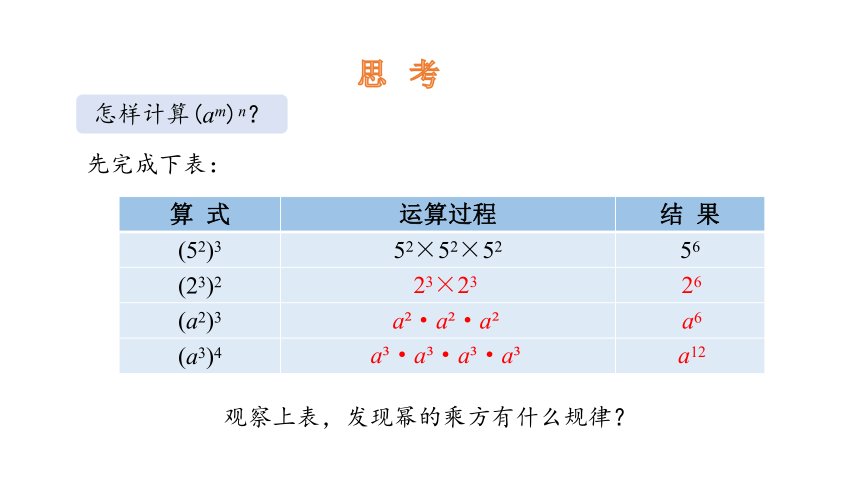
怎样计算(am)n?
先完成下表:
算 式 运算过程 结 果
(52)3 52×52×52 56
(23)2
(a2)3
(a3)4
23×23
26
a ·a ·a
a6
a ·a ·a ·a
a12
观察上表,发现幂的乘方有什么规律?
一般地,如果字母m,n都是正整数,那么
新课讲授
幂的乘方
(根据 ___ )
幂的意义
= amn
(根据____________________)
同底数幂的乘法法则
(am)n = am·am·…·am
n个am
= am+m+…+m
n个m
幂的乘方,底数不变,指数相乘.
幂的运算性质2:(am)n=amn(m,n都是正整数)
新课讲授
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星的半径是地球的10倍,它的体积是地球的10 倍!
太阳的半径是地球的10 倍,它的体积是地球的(10 ) 倍!
那么,你知道(10 ) 等于多少吗
根据幂的乘方的运算法则,可知(10 ) =10 ×10 ×10 =106.
教材例题
例 计算:
(1)(105)3; (2)(x4)2; (3)(-a2)3.
=105×105×105
=105+5+5
(根据 ___ )
幂的意义
=1015
(根据__________________)
同底数幂的乘法法则
=105×3
=(x4)·(x4)
=x4+4
=x8
=x4×2
=(-a )·(-a )·(-a )
=-a2+2+2
=-a6
=-a2×3
例题解读
例1 计算:(1)(102)3 ; (2)(b5)5; (3)(an)3;
(4)-(x2)m ; (5)(y2)3·y; (6)2(a2)6-(a3)4.
(6) 2(a2)6-(a3)4
=102×3
=106 ;
(1)(102)3
【解】
(2) (b5)5
= b5×5
= b25 ;
(3) (an)3
= an×3
=a3n ;
(4) -(x2)m
= -x2×m
= -x2m ;
(5) (y2)3·y
= y2×3·y
= y6·y
=2a2×6-a3×4
=2a12-a12
=a12.
= y7;
例题解读
例2 已知5x=m,5y=n,则52x+3y等于( )
A.2m+3n B.m2+n3
C.6mn D.m2n3
D
解析:因为5x=m,5y=n,
所以52x+3y=52x·53y=(5x)2·(5y)3=m2n3.
注意:
①同底数幂的乘法法则的逆用:am+n=am·an.
②幂的乘方法则的逆用:amn=(am)n=(an)m.
例题解读
例3 阅读下列解题过程:试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,16<27,
所以2100<375.
请根据上述方法解答问题:比较255,344,433的大小.
解:因为255=(25)11=3211,
344=(34)11=8111,433=(43)11=6411,
显然32<64<81,所以255<433<344.
1.下列4个算式中正确的有( )
①(a4)4=a4+4=a8;
②[(b2)2]2=b2×2×2=b8;
③[(-x)3]2=(-x)6=x6;
④(-y2)3=y6.
A.0个 B.1个
C.2个 D.3个
√
×
改正:a16
随堂练习
C
√
×
改正:-y6
本题易错之处在于混淆幂的乘方与同底数幂的乘法法则的运用.
随堂练习
幂的底数和指数不仅仅是单独字母或数字,也可以是某个单项式和多项式.
73×4=712
-y3×4=-y12
am×3=a3m
x3×2+5=x11
(-p)3×2+m=(-p)6+m
x3+1+2-3x2×2+2=-2x6
2. 计算:
随堂练习
3.已知a=833,b=1625,c=3219,试比较a,b,c的大小.
解:因为a=833=(23)33=299,
b=1625=(24)25=2100,
c=3219=(25)19=295,
显然95<99<100,
所以c<a<b.
课时小结
幂的运算性质1——同底数幂的乘法
幂的运算性质2——幂的乘方
am·an
=am+n
(m,n都是正整数)
(am) n=amn
(m,n都是正整数)
①同底数幂的乘法法则的逆用:am+n=am·an.
②幂的乘方法则的逆用:amn=(am)n=(an)m.
第八章 整式乘法与因式分解
8.1 幂的运算
8.1.2 幂的乘方与积的乘方
第1课时 幂的乘方
学习目标
1.理解幂的运算性质2,并掌握幂的乘方的运算.(重点)
2.运用幂的乘方解决实际问题.(难点)
3.正确区分幂的乘方与同底数幂的乘法.(难点)
知识回顾
幂的意义:
a×a×···×a = an
n个
幂同底数幂的乘法:
am·an=am+n(m,n都是正整数)
=(a·a·…·a)(a·a·…·a)
m个
n个
=(a·a·…·a)
(m+n)个
= am+n.
am·an
知识回顾
正方体的体积比与棱长比的关系
乙正方体的棱长是 2 cm, 则乙正方体的体积 V乙= cm3 .
V甲是V乙的 倍.
8
125
即 53 倍.
甲正方体的棱长是乙正方体的 5 倍,则甲正方体的棱长为_____cm,
甲正方体的体积V甲= cm3.
1 000
10
正方体的体积比=棱长比的立方
情境导入
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星
地球
太阳
情境导入
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星的半径是地球的10倍,它的体积是地球的10 倍!
太阳的半径是地球的10 倍,它的体积是地球的(10 ) 倍!
那么,你知道(10 ) 等于多少吗
思 考
怎样计算(am)n?
先完成下表:
算 式 运算过程 结 果
(52)3 52×52×52 56
(23)2
(a2)3
(a3)4
23×23
26
a ·a ·a
a6
a ·a ·a ·a
a12
观察上表,发现幂的乘方有什么规律?
一般地,如果字母m,n都是正整数,那么
新课讲授
幂的乘方
(根据 ___ )
幂的意义
= amn
(根据____________________)
同底数幂的乘法法则
(am)n = am·am·…·am
n个am
= am+m+…+m
n个m
幂的乘方,底数不变,指数相乘.
幂的运算性质2:(am)n=amn(m,n都是正整数)
新课讲授
地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星的半径是地球的10倍,它的体积是地球的10 倍!
太阳的半径是地球的10 倍,它的体积是地球的(10 ) 倍!
那么,你知道(10 ) 等于多少吗
根据幂的乘方的运算法则,可知(10 ) =10 ×10 ×10 =106.
教材例题
例 计算:
(1)(105)3; (2)(x4)2; (3)(-a2)3.
=105×105×105
=105+5+5
(根据 ___ )
幂的意义
=1015
(根据__________________)
同底数幂的乘法法则
=105×3
=(x4)·(x4)
=x4+4
=x8
=x4×2
=(-a )·(-a )·(-a )
=-a2+2+2
=-a6
=-a2×3
例题解读
例1 计算:(1)(102)3 ; (2)(b5)5; (3)(an)3;
(4)-(x2)m ; (5)(y2)3·y; (6)2(a2)6-(a3)4.
(6) 2(a2)6-(a3)4
=102×3
=106 ;
(1)(102)3
【解】
(2) (b5)5
= b5×5
= b25 ;
(3) (an)3
= an×3
=a3n ;
(4) -(x2)m
= -x2×m
= -x2m ;
(5) (y2)3·y
= y2×3·y
= y6·y
=2a2×6-a3×4
=2a12-a12
=a12.
= y7;
例题解读
例2 已知5x=m,5y=n,则52x+3y等于( )
A.2m+3n B.m2+n3
C.6mn D.m2n3
D
解析:因为5x=m,5y=n,
所以52x+3y=52x·53y=(5x)2·(5y)3=m2n3.
注意:
①同底数幂的乘法法则的逆用:am+n=am·an.
②幂的乘方法则的逆用:amn=(am)n=(an)m.
例题解读
例3 阅读下列解题过程:试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,16<27,
所以2100<375.
请根据上述方法解答问题:比较255,344,433的大小.
解:因为255=(25)11=3211,
344=(34)11=8111,433=(43)11=6411,
显然32<64<81,所以255<433<344.
1.下列4个算式中正确的有( )
①(a4)4=a4+4=a8;
②[(b2)2]2=b2×2×2=b8;
③[(-x)3]2=(-x)6=x6;
④(-y2)3=y6.
A.0个 B.1个
C.2个 D.3个
√
×
改正:a16
随堂练习
C
√
×
改正:-y6
本题易错之处在于混淆幂的乘方与同底数幂的乘法法则的运用.
随堂练习
幂的底数和指数不仅仅是单独字母或数字,也可以是某个单项式和多项式.
73×4=712
-y3×4=-y12
am×3=a3m
x3×2+5=x11
(-p)3×2+m=(-p)6+m
x3+1+2-3x2×2+2=-2x6
2. 计算:
随堂练习
3.已知a=833,b=1625,c=3219,试比较a,b,c的大小.
解:因为a=833=(23)33=299,
b=1625=(24)25=2100,
c=3219=(25)19=295,
显然95<99<100,
所以c<a<b.
课时小结
幂的运算性质1——同底数幂的乘法
幂的运算性质2——幂的乘方
am·an
=am+n
(m,n都是正整数)
(am) n=amn
(m,n都是正整数)
①同底数幂的乘法法则的逆用:am+n=am·an.
②幂的乘方法则的逆用:amn=(am)n=(an)m.
