8.2.1(2) 整式乘法-----单项式除以单项式 课件 (共24张PPT) 2023-2024学年数学沪科版七年级下册
文档属性
| 名称 | 8.2.1(2) 整式乘法-----单项式除以单项式 课件 (共24张PPT) 2023-2024学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 369.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 23:41:56 | ||
图片预览








文档简介
(共24张PPT)
第八章 整式乘法与因式分解
8.2 整式乘法
8.2.1 单项式与单项式相乘
第2课时 单项式除以单项式
学习目标
1.理解单项式除以单项式的含义,并掌握单项式除以单项式的运算法则.(重点)
2.能运用单项式除以单项式进行计算并解决问题.(难点)
知识回顾
1.同底数幂的除法法则
同底数幂相除,底数不变,指数相减.
am÷an
= am-n
(a≠0,m,n都是正整数,m>n)
逆用:am-n=am÷an(a≠0,m,n都是正整数,m>n)
推广:am÷an÷ap=am-n-p
知识回顾
2.单项式乘单项式的运算法则
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
试着填一填:
(1)am·an=________; (2)(am)n=________;
(3)am+n÷an=________;(4)amn÷an=________.
am+n
amn
am
amn-n
思 考
怎样计算15a4b3x2÷3a2b3?
计算15a4b3x2÷3a2b3,就是要求一个单项式,使它与3a2b3相乘的积等于15a4b3x2.
因为 (5a2x2)·(3a2b3)=15a4b3x2,
所以 15a4b3x2÷3a2b3=5a2x2.
分析所得式子,能得到什么规律?
思 考
怎样计算15a4b3x2÷3a2b3?
15a4b3x2÷3a2b3=5a2x2.
结果中的5=15÷3;
结果中的a2=a4÷a2=a4-2;
结果中的x2=x2÷1;
因为被除式与除式中都有b3,b3÷b3=1,所以结果中没有b.
分析可得:
同底数幂的除法
举例探究
计算下列各题.
⑴(x5y)÷x2; ⑵(8m n2)÷(2m2n).
小学里学过分数的约分,可以把除法变成分数,再约分!
(8m n2)÷(2m2n)
=
=
(x5y)÷x2
==
=.
知识探究
(1)商式的系数与被除式、除式的系数有什么关系?
(2)被除式、除式中相同字母及其指数在商式的变化规律是什么?
(3)被除式中含有的字母,除式中没有的字母及其指数在商式中有
没有变化?
商式的系数等于被除式的系数除以除式的系数.
对于相同字母,商式中的指数等于被除式中的指数减去除式中的指数.
没有变化.
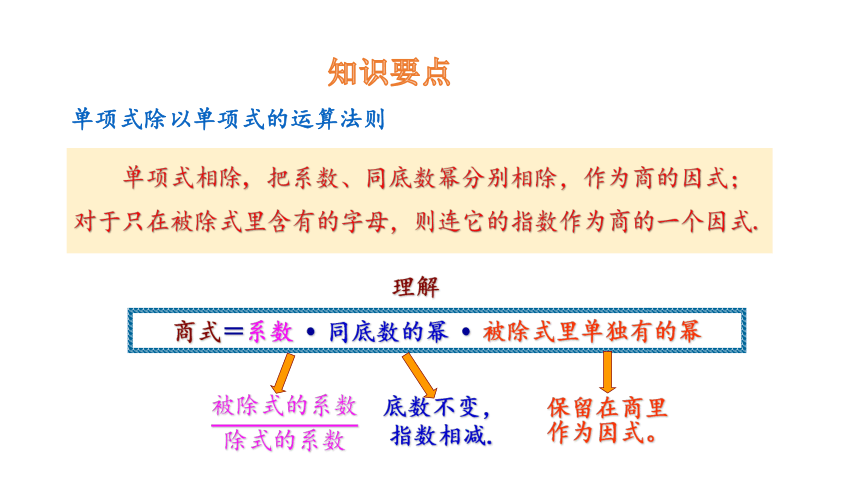
知识要点
单项式除以单项式的运算法则
单项式相除, 把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连它的指数作为商的一个因式.
理解
商式=系数 同底数的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里
作为因式。
教材例题
例1 计算:
(1)32x5y3÷8x3y; (2)-7a8b4c2÷49a7b4.
解:32x5y3÷8x3y
=(32÷8)·x5-3y3-1
=4x2y2
-7a8b4c2÷49a7b4
=[(-7)÷49]·a8-7b4-4c2
=ac2
注意:在计算系数相除时,不要漏掉前面的符号“-”.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(1)它的这一行程相当于地球赤道多少圈?(已知地球半径约6.4×10 km,π取3.14)
解:根据题意,可列式为
3.5×109÷(2×3.14×6.4×103)
≈8.7×104(圈).
探测器的行程相当于地球赤道约87 000圈.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(2)这一行程如果由速度是100km/h的汽车来完成,需要行驶多少年?(1年按365天计算)
解:根据题意,可列式为
3.5×109÷(365×24×100)
≈4.0×103(年).
探测器的行程相当于由速度为100km/h的汽车行驶约4 000年.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(3)这一行程如果由速度是10m/s的短跑飞人来完成,需要跑多少年?
解:根据题意,可列式为
3.5×109÷(365×24×3.6×103×10×10-3)
≈1.1×104(年).
探测器的行程相当于由速度为10m/s的短跑飞人跑约11 000年.
例题解读
例1 计算:
(1)x2y3÷(3x2y); (2)(10a4b3c2)÷(5a3bc);
(1)原式=()·x2-2y3-1
=y2
(2)原式=()·a4-3b3-1c2-1
=2ab2c
例题解读
例1 计算:
(3)(2x2y)3·(-7xy2)÷(14x4y3).
(3)原式=8x6y3·(-7xy2)÷(14x4y3)
=-56x7y5÷(14x4y3)
=-4x y
注意:(3)题,在混合运算中要注意运算顺序,先乘方,再乘除,后加减;
例题解读
例2 若a(xmy4)3÷(3x2yn)2=4x2y2,求a、m、n的值.
解:因为a(xmy4)3÷(3x2yn)2=4x2y2,
所以ax3my12÷9x4y2n=4x2y2,
所以a÷9=4,3m-4=2,12-2n=2,
解得a=36,m=2,n=5.
分析:利用积的乘方的计算法则以及整式的除法运算得出即可.
随堂练习
1.(重庆中考)计算3a6÷a的结果是( )
A.3a6 B.2a5 C.2a6 D.3a5
D
2.如果“□×2ab=4a2b”,那么“□”内应填的代数式是( )
A.2b B.2ab C.a D.2a
D
3.已知a=1.6×109,b=4×103,则a2÷b的结果为( )
A.4×107 B.8×1014 C.6.4×105 D.6.4×1014
D
随堂练习
4.计算:
(1)(a3x3)÷(-ax2); (2)(3a2b3c)3÷(-6a5b3);
随堂练习
4.计算:
(3)(3x2)3·(4y3)2÷(6xy)3; (4)(12x5y6z4)÷(-3x2y2z)÷(2x3y3z2);
随堂练习
4.计算:
(5)(-3a b c) ·(2ac )÷(-18a4b5)÷(3a c ) .
随堂练习
5. 2022年6月28日金沙江巨型水电站全国爱国主义教育示范基地开放日活动暨《水电建设》特种邮票首发仪式在白鹤滩水电站举行。白鹤滩水电站自2021年开始实现发电以来,截止到2022年6月,累计发电量已经达到290亿千瓦时,若某市有10万户居民,平均每户居民每年用电1.45×103千瓦时。那么白鹤滩水电站累计发电量可供该市居民使用多少年?
解:该市年用电量为1.45×103×105=1.45×108(千瓦时),
(2.9×1010)÷(1.45×108)=(2.9÷1.45)×1010-8=200(年).
答:白鹤滩水电站累积发电量可供该市居民使用200年.
均用科学记数法表示.
随堂练习
6.若 3x = 5,3y = 4,求 32x-y 的值.
解:32x-y = 32x÷3y
= (3x)2÷3y
= 52÷4
=.
课时小结
单项式除以单项式的运算法则
单项式相除, 把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连它的指数作为商的一个因式.
归纳总结
通过填表的方式对比学习:
单项式乘单项式 单项式除以单项式
第一步 系数相乘 系数相除
第二步 同底数幂相乘 同底数幂相除
第三步 其余字母连同它的指数不变,作为积的因式 只在被除式里含有的字母连同它的指数一起作为商的一个因式
第八章 整式乘法与因式分解
8.2 整式乘法
8.2.1 单项式与单项式相乘
第2课时 单项式除以单项式
学习目标
1.理解单项式除以单项式的含义,并掌握单项式除以单项式的运算法则.(重点)
2.能运用单项式除以单项式进行计算并解决问题.(难点)
知识回顾
1.同底数幂的除法法则
同底数幂相除,底数不变,指数相减.
am÷an
= am-n
(a≠0,m,n都是正整数,m>n)
逆用:am-n=am÷an(a≠0,m,n都是正整数,m>n)
推广:am÷an÷ap=am-n-p
知识回顾
2.单项式乘单项式的运算法则
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
试着填一填:
(1)am·an=________; (2)(am)n=________;
(3)am+n÷an=________;(4)amn÷an=________.
am+n
amn
am
amn-n
思 考
怎样计算15a4b3x2÷3a2b3?
计算15a4b3x2÷3a2b3,就是要求一个单项式,使它与3a2b3相乘的积等于15a4b3x2.
因为 (5a2x2)·(3a2b3)=15a4b3x2,
所以 15a4b3x2÷3a2b3=5a2x2.
分析所得式子,能得到什么规律?
思 考
怎样计算15a4b3x2÷3a2b3?
15a4b3x2÷3a2b3=5a2x2.
结果中的5=15÷3;
结果中的a2=a4÷a2=a4-2;
结果中的x2=x2÷1;
因为被除式与除式中都有b3,b3÷b3=1,所以结果中没有b.
分析可得:
同底数幂的除法
举例探究
计算下列各题.
⑴(x5y)÷x2; ⑵(8m n2)÷(2m2n).
小学里学过分数的约分,可以把除法变成分数,再约分!
(8m n2)÷(2m2n)
=
=
(x5y)÷x2
==
=.
知识探究
(1)商式的系数与被除式、除式的系数有什么关系?
(2)被除式、除式中相同字母及其指数在商式的变化规律是什么?
(3)被除式中含有的字母,除式中没有的字母及其指数在商式中有
没有变化?
商式的系数等于被除式的系数除以除式的系数.
对于相同字母,商式中的指数等于被除式中的指数减去除式中的指数.
没有变化.
知识要点
单项式除以单项式的运算法则
单项式相除, 把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连它的指数作为商的一个因式.
理解
商式=系数 同底数的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里
作为因式。
教材例题
例1 计算:
(1)32x5y3÷8x3y; (2)-7a8b4c2÷49a7b4.
解:32x5y3÷8x3y
=(32÷8)·x5-3y3-1
=4x2y2
-7a8b4c2÷49a7b4
=[(-7)÷49]·a8-7b4-4c2
=ac2
注意:在计算系数相除时,不要漏掉前面的符号“-”.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(1)它的这一行程相当于地球赤道多少圈?(已知地球半径约6.4×10 km,π取3.14)
解:根据题意,可列式为
3.5×109÷(2×3.14×6.4×103)
≈8.7×104(圈).
探测器的行程相当于地球赤道约87 000圈.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(2)这一行程如果由速度是100km/h的汽车来完成,需要行驶多少年?(1年按365天计算)
解:根据题意,可列式为
3.5×109÷(365×24×100)
≈4.0×103(年).
探测器的行程相当于由速度为100km/h的汽车行驶约4 000年.
教材例题
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道.
(3)这一行程如果由速度是10m/s的短跑飞人来完成,需要跑多少年?
解:根据题意,可列式为
3.5×109÷(365×24×3.6×103×10×10-3)
≈1.1×104(年).
探测器的行程相当于由速度为10m/s的短跑飞人跑约11 000年.
例题解读
例1 计算:
(1)x2y3÷(3x2y); (2)(10a4b3c2)÷(5a3bc);
(1)原式=()·x2-2y3-1
=y2
(2)原式=()·a4-3b3-1c2-1
=2ab2c
例题解读
例1 计算:
(3)(2x2y)3·(-7xy2)÷(14x4y3).
(3)原式=8x6y3·(-7xy2)÷(14x4y3)
=-56x7y5÷(14x4y3)
=-4x y
注意:(3)题,在混合运算中要注意运算顺序,先乘方,再乘除,后加减;
例题解读
例2 若a(xmy4)3÷(3x2yn)2=4x2y2,求a、m、n的值.
解:因为a(xmy4)3÷(3x2yn)2=4x2y2,
所以ax3my12÷9x4y2n=4x2y2,
所以a÷9=4,3m-4=2,12-2n=2,
解得a=36,m=2,n=5.
分析:利用积的乘方的计算法则以及整式的除法运算得出即可.
随堂练习
1.(重庆中考)计算3a6÷a的结果是( )
A.3a6 B.2a5 C.2a6 D.3a5
D
2.如果“□×2ab=4a2b”,那么“□”内应填的代数式是( )
A.2b B.2ab C.a D.2a
D
3.已知a=1.6×109,b=4×103,则a2÷b的结果为( )
A.4×107 B.8×1014 C.6.4×105 D.6.4×1014
D
随堂练习
4.计算:
(1)(a3x3)÷(-ax2); (2)(3a2b3c)3÷(-6a5b3);
随堂练习
4.计算:
(3)(3x2)3·(4y3)2÷(6xy)3; (4)(12x5y6z4)÷(-3x2y2z)÷(2x3y3z2);
随堂练习
4.计算:
(5)(-3a b c) ·(2ac )÷(-18a4b5)÷(3a c ) .
随堂练习
5. 2022年6月28日金沙江巨型水电站全国爱国主义教育示范基地开放日活动暨《水电建设》特种邮票首发仪式在白鹤滩水电站举行。白鹤滩水电站自2021年开始实现发电以来,截止到2022年6月,累计发电量已经达到290亿千瓦时,若某市有10万户居民,平均每户居民每年用电1.45×103千瓦时。那么白鹤滩水电站累计发电量可供该市居民使用多少年?
解:该市年用电量为1.45×103×105=1.45×108(千瓦时),
(2.9×1010)÷(1.45×108)=(2.9÷1.45)×1010-8=200(年).
答:白鹤滩水电站累积发电量可供该市居民使用200年.
均用科学记数法表示.
随堂练习
6.若 3x = 5,3y = 4,求 32x-y 的值.
解:32x-y = 32x÷3y
= (3x)2÷3y
= 52÷4
=.
课时小结
单项式除以单项式的运算法则
单项式相除, 把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连它的指数作为商的一个因式.
归纳总结
通过填表的方式对比学习:
单项式乘单项式 单项式除以单项式
第一步 系数相乘 系数相除
第二步 同底数幂相乘 同底数幂相除
第三步 其余字母连同它的指数不变,作为积的因式 只在被除式里含有的字母连同它的指数一起作为商的一个因式
