2.4 过不共线三点作圆 课件 (共21张PPT)2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.4 过不共线三点作圆 课件 (共21张PPT)2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 236.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 11:05:16 | ||
图片预览






文档简介
(共21张PPT)
第2章 圆
2.4 过不共线三点作圆
1.经历不在同一直线上的三个点确定一个圆的探索过程.
2.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法.(重难点)
3.了解三角形的外接圆、三角形的外心等概念.
学习目标
课时导入
问题1 如何过一个点 A 作一个圆?过点 A 可以作多少个圆?
议一议
·
·
·
·
·
以不与点 A 重合的任意一点为圆心,以这个点到 点 A 的距离为半径画圆即可;过点A可作无数个圆.
A
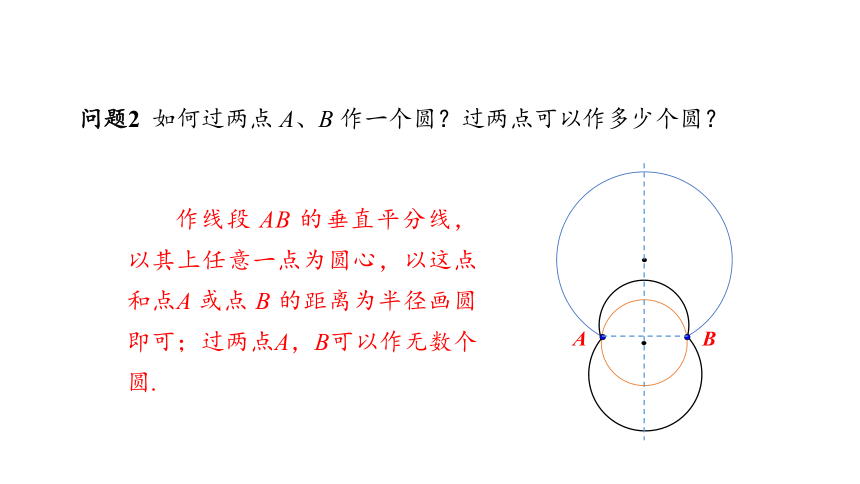
问题2 如何过两点 A、B 作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
作线段 AB 的垂直平分线,以其上任意一点为圆心,以这点和点A 或点 B 的距离为半径画圆即可;过两点A,B可以作无数个圆.
N
M
F
E
O
A
B
C
问题3 经过不在同一直线上的三个已知点 A,B,C 能作圆吗?
假设经过 A、B、C 三点的☉O 存在.
(1)圆心 O 到 A、B、C 三点距离 .
(填“相等”或”不相等”).
(2)如果 O 点到 A、B 的距离相等,则点 O 应在线段 AB 的__________上,同理点 O 也应在线段 AC 的__________上.
(3)点 O 应是线段 AB、AC 的____________的交点,半径为 OA 的长,所以_____作圆.
相等
垂直平分线
垂直平分线
垂直平分线
能
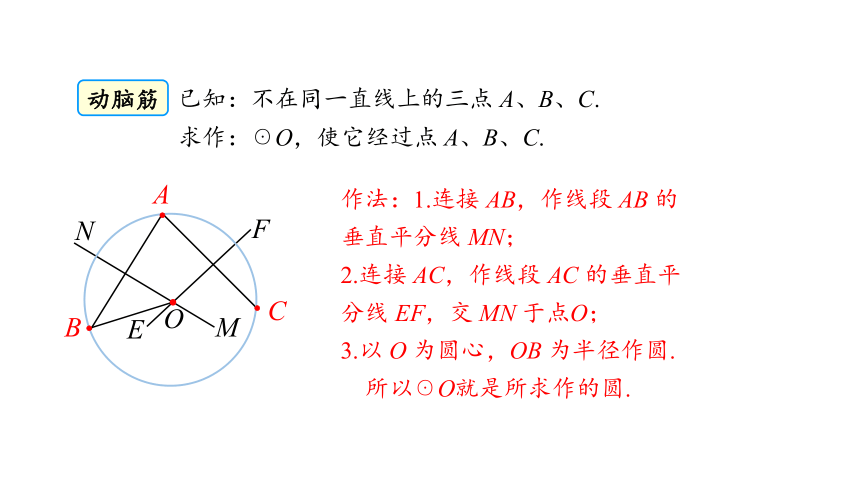
已知:不在同一直线上的三点 A、B、C.
求作:☉O,使它经过点 A、B、C.
作法:1.连接 AB,作线段 AB 的垂直平分线 MN;
2.连接 AC,作线段 AC 的垂直平分线 EF,交 MN 于点O;
3.以 O 为圆心,OB 为半径作圆.
所以☉O就是所求作的圆.
O
N
M
F
E
A
B
C
动脑筋
A
B
C
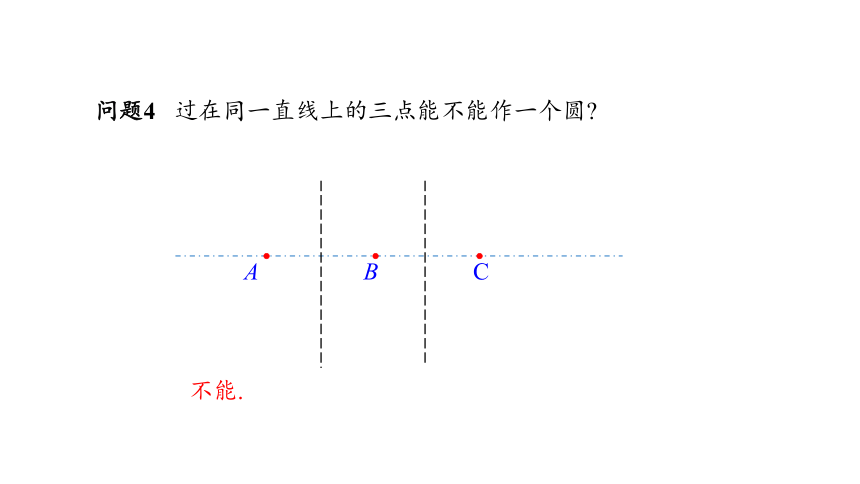
问题4 过在同一直线上的三点能不能作一个圆
不能.
知识讲解
经过不在同一直线上的三点可以作一个圆而且只能作一个圆.
说一说
问题5 经过 △ABC 的三个顶点可以作一个圆吗?
由于△ABC 的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.
知识讲解
1. 外接圆
经过三角形各顶点的圆叫作这个三角形的外接圆.☉O 叫作△ABC 的________, 这个三角形叫作这个圆的内接三角形,△ABC 叫作☉O 的____________.
三角形的外心到三角形三个顶点的距离相等.
2. 三角形的外心:
定义:
外接圆
内接三角形
三角形外接圆的圆心叫作三角形的外心.
作图:
三角形三条边的垂直平分线的交点.
性质:
●O
A
B
C
1.分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
练习
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
三角形外心的位置:
2.你知道如何将一个破损的圆盘复原吗?
A
B
C
O
方法:
1.在圆弧上任取三点 A、B、C;
2.连接 AB、BC,作线段 AB、BC 的垂直平分线,其交点 O 即为圆心;
3.以点 O 为圆心,OC 长为半径作圆.
☉O 即为所求.
随 堂 小 测
1.如图,☉O是 △ABC 的外接圆,半径为 2 cm,若 BC=2 cm,
则∠A 的度数为( )
A.30° B.25° C.15° D.10°
A
2.小颖同学在手工制作中,把一个边长为 12 cm 的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. cm B. cm
C. cm D. cm
B
3. 三角形的外心具有的性质是( )
A. 到三边的距离相等
B. 到三个顶点的距离相等
C. 外心在三角形的外
D. 外心在三角形内
B
4.10个大小相同的正六边形按如图所示方式紧密排列在同一
平面内,A,B,C,D,E,O均是正六边形的顶点,则点O
是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
D
5. 如图,直角坐标系中一条圆弧经过网格点 A、B、C,其中,B点坐标为 (4,4),则该圆弧所在圆的圆心坐标为__________.
(2,0)
6.下列说法是否正确.
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
(5)三角形的外心就是这个三角形两边垂直平分线的交点.( )
(6)等腰三角形的外心一定在这个三角形内 .( )
√
×
×
√
√
×
7. 某一个城市在一块空地新建了三个居民小区,它们分别为 A、
B、C,且三个小区不在同一直线上,要想规划一所中学,使这所
中学到三个小区的距离相等. 请问同学们, 这所中学建在哪个位
置?你怎么确定这个位置呢?
●
●
●
B
A
C
试着在草稿纸上画一下~
小结
3. 锐角三角形
直角三角形 --外心的位置--
钝角三角形
1.作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
2. 经过三角形的三个顶点的圆叫作三角形的外接圆;
外接圆的圆心叫作三角形的外心;
这个三角形叫作圆的内接三角形.
在斜边的中点
在三角形的内部
在三角形的外部
第2章 圆
2.4 过不共线三点作圆
1.经历不在同一直线上的三个点确定一个圆的探索过程.
2.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法.(重难点)
3.了解三角形的外接圆、三角形的外心等概念.
学习目标
课时导入
问题1 如何过一个点 A 作一个圆?过点 A 可以作多少个圆?
议一议
·
·
·
·
·
以不与点 A 重合的任意一点为圆心,以这个点到 点 A 的距离为半径画圆即可;过点A可作无数个圆.
A
问题2 如何过两点 A、B 作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
作线段 AB 的垂直平分线,以其上任意一点为圆心,以这点和点A 或点 B 的距离为半径画圆即可;过两点A,B可以作无数个圆.
N
M
F
E
O
A
B
C
问题3 经过不在同一直线上的三个已知点 A,B,C 能作圆吗?
假设经过 A、B、C 三点的☉O 存在.
(1)圆心 O 到 A、B、C 三点距离 .
(填“相等”或”不相等”).
(2)如果 O 点到 A、B 的距离相等,则点 O 应在线段 AB 的__________上,同理点 O 也应在线段 AC 的__________上.
(3)点 O 应是线段 AB、AC 的____________的交点,半径为 OA 的长,所以_____作圆.
相等
垂直平分线
垂直平分线
垂直平分线
能
已知:不在同一直线上的三点 A、B、C.
求作:☉O,使它经过点 A、B、C.
作法:1.连接 AB,作线段 AB 的垂直平分线 MN;
2.连接 AC,作线段 AC 的垂直平分线 EF,交 MN 于点O;
3.以 O 为圆心,OB 为半径作圆.
所以☉O就是所求作的圆.
O
N
M
F
E
A
B
C
动脑筋
A
B
C
问题4 过在同一直线上的三点能不能作一个圆
不能.
知识讲解
经过不在同一直线上的三点可以作一个圆而且只能作一个圆.
说一说
问题5 经过 △ABC 的三个顶点可以作一个圆吗?
由于△ABC 的三个顶点不在同一直线上,因此过这三个顶点可以作一个圆,并且只可以作一个圆.
知识讲解
1. 外接圆
经过三角形各顶点的圆叫作这个三角形的外接圆.☉O 叫作△ABC 的________, 这个三角形叫作这个圆的内接三角形,△ABC 叫作☉O 的____________.
三角形的外心到三角形三个顶点的距离相等.
2. 三角形的外心:
定义:
外接圆
内接三角形
三角形外接圆的圆心叫作三角形的外心.
作图:
三角形三条边的垂直平分线的交点.
性质:
●O
A
B
C
1.分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
练习
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
三角形外心的位置:
2.你知道如何将一个破损的圆盘复原吗?
A
B
C
O
方法:
1.在圆弧上任取三点 A、B、C;
2.连接 AB、BC,作线段 AB、BC 的垂直平分线,其交点 O 即为圆心;
3.以点 O 为圆心,OC 长为半径作圆.
☉O 即为所求.
随 堂 小 测
1.如图,☉O是 △ABC 的外接圆,半径为 2 cm,若 BC=2 cm,
则∠A 的度数为( )
A.30° B.25° C.15° D.10°
A
2.小颖同学在手工制作中,把一个边长为 12 cm 的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. cm B. cm
C. cm D. cm
B
3. 三角形的外心具有的性质是( )
A. 到三边的距离相等
B. 到三个顶点的距离相等
C. 外心在三角形的外
D. 外心在三角形内
B
4.10个大小相同的正六边形按如图所示方式紧密排列在同一
平面内,A,B,C,D,E,O均是正六边形的顶点,则点O
是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
D
5. 如图,直角坐标系中一条圆弧经过网格点 A、B、C,其中,B点坐标为 (4,4),则该圆弧所在圆的圆心坐标为__________.
(2,0)
6.下列说法是否正确.
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
(5)三角形的外心就是这个三角形两边垂直平分线的交点.( )
(6)等腰三角形的外心一定在这个三角形内 .( )
√
×
×
√
√
×
7. 某一个城市在一块空地新建了三个居民小区,它们分别为 A、
B、C,且三个小区不在同一直线上,要想规划一所中学,使这所
中学到三个小区的距离相等. 请问同学们, 这所中学建在哪个位
置?你怎么确定这个位置呢?
●
●
●
B
A
C
试着在草稿纸上画一下~
小结
3. 锐角三角形
直角三角形 --外心的位置--
钝角三角形
1.作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
2. 经过三角形的三个顶点的圆叫作三角形的外接圆;
外接圆的圆心叫作三角形的外心;
这个三角形叫作圆的内接三角形.
在斜边的中点
在三角形的内部
在三角形的外部
