2.5.1 直线与圆的位置关系 课件(共22张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.5.1 直线与圆的位置关系 课件(共22张PPT) 2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 705.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 11:12:13 | ||
图片预览








文档简介
(共22张PPT)
第2章 圆
2.5 直线与圆的位置关系
2.5.1 直线与圆的位置关系
1.了解直线与圆的三种位置关系.(重点)
2.能通过比较圆心到直线的距离与半径之间的数量关系来揭示直线与圆的位置关系.(难点)
3.经历探索直线与圆的位置关系的过程,加深对分类、数形结合等数学思想方法的理解.
4.掌握切线的概念.
学习目标
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d知识回顾
课时导入
观察
问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
问题2 如图,在纸上画一条直线 l,把钥匙环看作一个圆. 在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
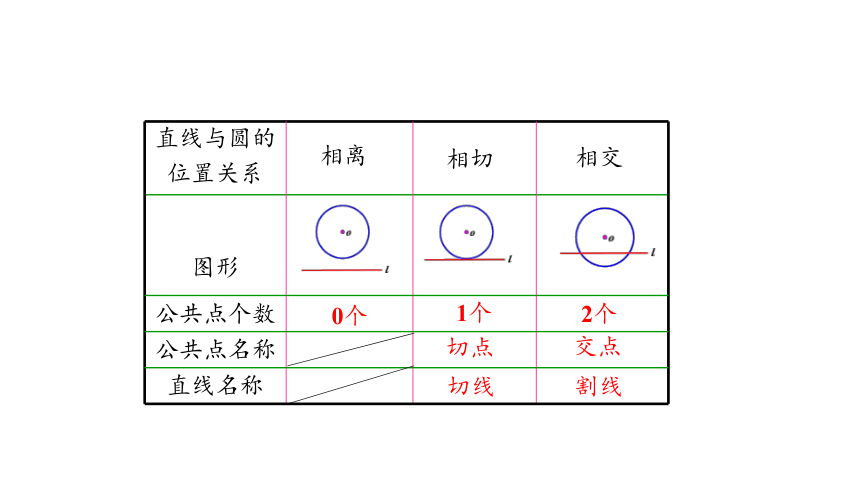
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫作圆的割线.
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫作圆的切线,这个点叫作切点.
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
如何用数量关系来度量这种位置关系呢?
O
d
用圆心到直线的距离d与半径r的大小关系来判断直线与圆的位置关系.
r
直线和圆相交
d < r
直线和圆相切
d = r
直线和圆相离
d > r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
用圆心 O 到直线的距离 d 与圆的半径 r 的关系来区分
o
o
o
直线与圆的位置关系
的性质与判定的区别:
位置关系 数量关系.
公共点个数
如图,∠C = 30°,O 为 BC 上一点,且CO = 6 cm,以 O 为圆心,r 为半径的圆与直线 CA 有怎样的位置关系?为什么?
(1)r = 2.5 cm; (2)r = 3 cm; (3)r = 5 cm.
解:过 O 点作 OD⊥CA 交 CA于 D.
A
B
C
D
O
在Rt△CDO中, ∠C = 30°,
例
即圆心 O 到直线 CA 的距离 d = 3 cm.
(1)r = 2.5 cm 时,有 d > r,因此☉O 与直线 CA 相离;
(2)r = 3 cm 时,有 d = r,因此☉O 与直线 CA 相切;
(3)r = 5 cm 时,有 d < r,因此☉O 与直线 CA 相交.
随 堂 小 测
1.已知☉O的半径是6,点O到直线l的距离为5,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2.直线l与半径为r的☉O相离,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
C
A
状元成才
3.如图,在 Rt△ABC 中,∠ACB = 90°,∠B = 30°,BC = 4 cm,以点 C 为圆心,2 cm 为半径作圆,则☉C 与 AB 的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
B
解:如图,过点 C 作 CH⊥AB 于点 H ,
在 Rt△CHB 中,易得 CH = 2 cm,即 d = r = 2 cm,
所以☉C 与 AB 的位置关系是相切.
4. 在 Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心,r 为半径作圆,
(1) 当 r 满足________________时,
☉C与直线 AB 相离.
(2) 当 r 满足____________ 时,
☉C与直线 AB 相切.
(3) 当 r 满足____________时,
☉C与直线 AB 相交.
B
C
A
4
5
3
0< r <2.4
r = 2.4
r > 2.4
5.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为 .
解:若与OA,AB,BC三条边相切,D的坐标为(3,1);
若与OA,BC,CO三条边相切,D的坐标为(1,1);
若与OA,AB,CO三条边相切,D的坐标为(2,2);
若与AB,BC,CO三条边相切,D的坐标为(2,0).
(1,1),(3,1),(2,2)和(2,0)
6. 如图,∠APB = 30°,圆心在 PB 上的☉O 的半径为 1 cm,OP = 3 cm,若☉O 沿 BP 方向平移,当☉O 与 PA 相切时,圆心 O 平移的距离为_____________.
1cm 或 5 cm
7.某市计划在学校 C 的不远处修建一条东西方向的马路 ,要求学校周围 240 m 的范围内不能有噪声. 如图所示,学校北偏东45°的地方是一个勘测点 A ,北偏西 60°的地方是另一个勘测点 B ,两个勘测点之间的距离为 540 m ,为了使马路上行车的噪声不影响学校,沿 AB 方向修建马路是否符合要求?(参考数据:≈1.7)
比较学校到马路的最短距离与240 m的大小即可.
解:如图,过点 C 作 CD⊥AB 于点 D .
设 CD = x m .
∵∠ACD = 45°,∠BCD = 60°,
∴AD = x m,BC = 2x m,
∴BD = x (m).
∵AB = 540 m,∴ x + x = 540,∴x ≈ 200.
∵200 < 240,∴沿 AB 方向修建马路不符合要求.
D
小结
直线与圆的位置关系
定义
性质
判定
相离、相切、相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d0个:相离
1个:相切
2个:相交
d>r:相离
d=r:相切
d相离:0个
相切:1个
相交:2个
第2章 圆
2.5 直线与圆的位置关系
2.5.1 直线与圆的位置关系
1.了解直线与圆的三种位置关系.(重点)
2.能通过比较圆心到直线的距离与半径之间的数量关系来揭示直线与圆的位置关系.(难点)
3.经历探索直线与圆的位置关系的过程,加深对分类、数形结合等数学思想方法的理解.
4.掌握切线的概念.
学习目标
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
课时导入
观察
问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
问题2 如图,在纸上画一条直线 l,把钥匙环看作一个圆. 在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫作圆的割线.
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫作圆的切线,这个点叫作切点.
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
如何用数量关系来度量这种位置关系呢?
O
d
用圆心到直线的距离d与半径r的大小关系来判断直线与圆的位置关系.
r
直线和圆相交
d < r
直线和圆相切
d = r
直线和圆相离
d > r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
用圆心 O 到直线的距离 d 与圆的半径 r 的关系来区分
o
o
o
直线与圆的位置关系
的性质与判定的区别:
位置关系 数量关系.
公共点个数
如图,∠C = 30°,O 为 BC 上一点,且CO = 6 cm,以 O 为圆心,r 为半径的圆与直线 CA 有怎样的位置关系?为什么?
(1)r = 2.5 cm; (2)r = 3 cm; (3)r = 5 cm.
解:过 O 点作 OD⊥CA 交 CA于 D.
A
B
C
D
O
在Rt△CDO中, ∠C = 30°,
例
即圆心 O 到直线 CA 的距离 d = 3 cm.
(1)r = 2.5 cm 时,有 d > r,因此☉O 与直线 CA 相离;
(2)r = 3 cm 时,有 d = r,因此☉O 与直线 CA 相切;
(3)r = 5 cm 时,有 d < r,因此☉O 与直线 CA 相交.
随 堂 小 测
1.已知☉O的半径是6,点O到直线l的距离为5,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2.直线l与半径为r的☉O相离,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
C
A
状元成才
3.如图,在 Rt△ABC 中,∠ACB = 90°,∠B = 30°,BC = 4 cm,以点 C 为圆心,2 cm 为半径作圆,则☉C 与 AB 的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
B
解:如图,过点 C 作 CH⊥AB 于点 H ,
在 Rt△CHB 中,易得 CH = 2 cm,即 d = r = 2 cm,
所以☉C 与 AB 的位置关系是相切.
4. 在 Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心,r 为半径作圆,
(1) 当 r 满足________________时,
☉C与直线 AB 相离.
(2) 当 r 满足____________ 时,
☉C与直线 AB 相切.
(3) 当 r 满足____________时,
☉C与直线 AB 相交.
B
C
A
4
5
3
0< r <2.4
r = 2.4
r > 2.4
5.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为 .
解:若与OA,AB,BC三条边相切,D的坐标为(3,1);
若与OA,BC,CO三条边相切,D的坐标为(1,1);
若与OA,AB,CO三条边相切,D的坐标为(2,2);
若与AB,BC,CO三条边相切,D的坐标为(2,0).
(1,1),(3,1),(2,2)和(2,0)
6. 如图,∠APB = 30°,圆心在 PB 上的☉O 的半径为 1 cm,OP = 3 cm,若☉O 沿 BP 方向平移,当☉O 与 PA 相切时,圆心 O 平移的距离为_____________.
1cm 或 5 cm
7.某市计划在学校 C 的不远处修建一条东西方向的马路 ,要求学校周围 240 m 的范围内不能有噪声. 如图所示,学校北偏东45°的地方是一个勘测点 A ,北偏西 60°的地方是另一个勘测点 B ,两个勘测点之间的距离为 540 m ,为了使马路上行车的噪声不影响学校,沿 AB 方向修建马路是否符合要求?(参考数据:≈1.7)
比较学校到马路的最短距离与240 m的大小即可.
解:如图,过点 C 作 CD⊥AB 于点 D .
设 CD = x m .
∵∠ACD = 45°,∠BCD = 60°,
∴AD = x m,BC = 2x m,
∴BD = x (m).
∵AB = 540 m,∴ x + x = 540,∴x ≈ 200.
∵200 < 240,∴沿 AB 方向修建马路不符合要求.
D
小结
直线与圆的位置关系
定义
性质
判定
相离、相切、相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d
1个:相切
2个:相交
d>r:相离
d=r:相切
d
相切:1个
相交:2个
