2.5.2 第1课时 切线的判定 课件 (共16张PPT)2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.5.2 第1课时 切线的判定 课件 (共16张PPT)2023-2024学年数学湘教版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 11:16:35 | ||
图片预览






文档简介
(共16张PPT)
第2章 圆
2.5.2 圆的切线
第1课时 切线的判定
2.5 直线与圆的位置关系
1.探索切线与过切点的半径的关系,理解切线的判定定理.(重难点)
2.运用切线的判定定理,用三角尺过圆上一点画圆的切线.
学习目标
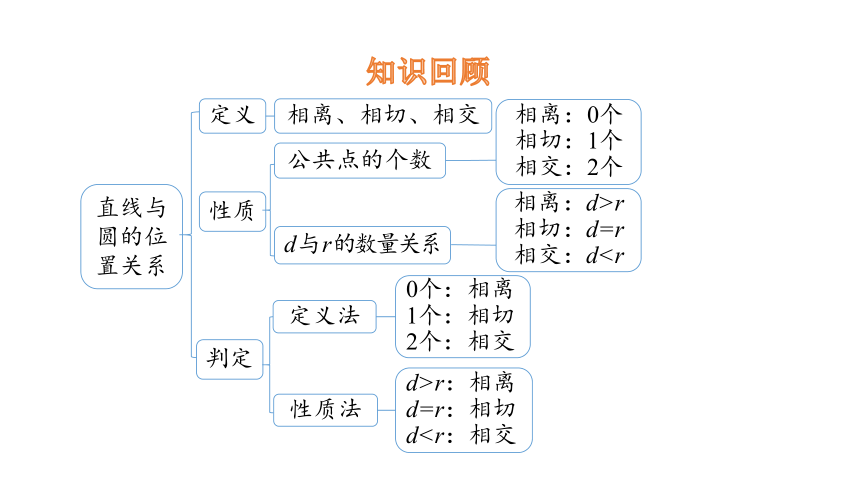
知识回顾
直线与圆的位置关系
定义
性质
判定
相离、相切、相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d0个:相离
1个:相切
2个:相交
d>r:相离
d=r:相切
d相离:0个
相切:1个
相交:2个
课时导入
观察
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中,我们常常看到切线的实例,如何判断一条直线是否为圆的切线呢?
探究
如图,OA 是☉O 的半径,经过 OA 的外端点 A,作一条直线 l ⊥ OA,圆心 O 到直线 l 的距离是多少?直线 l 和☉O 有怎样的位置关系?
l
圆心 O 到直线 l 的
距离等于半径 OA.
由圆的切线定义可知直线 l 与☉O 相切.
l
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为☉O 的半径
BC ⊥ OA 于 A
BC 为☉O 的切线
A
B
C
切线的判定定理
O
知识讲解
!在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
用三角尺过圆上一点画圆的切线.
(2) 过点 P 沿着三角尺的另一条直角边画直线 l,
则 l 就是所要画的切线.如图.
已知☉O 上一点 P,过点 P 画☉O 的切线.
画法:(1) 连接 OP,将三角尺的直角顶点放在点 P 处,
并使一直角边与半径 OP 重合;
为什么画出来的直线l 是☉O 的切线呢?
做一做
例
如图,已知 AD 是☉O 的直径,直线 BC 经过点 D,并且 AB = AC ,∠BAD =∠CAD. 求证:直线 BC 是☉O 的切线.
D
证明:∵ AB = AC,∠BAD = ∠CAD,
∴ AD ⊥ BC.
又∵ OD 是☉O 的半径,且 BC 经过点 D,
∴ 直线 BC 是☉O 的切线.
(1)已明确直线和圆有公共点,连接圆心和公共点,即半径,再证直线与半径垂直.简记“有交点,连半径,证垂直”;
(2)不明确直线和圆有无公共点,先过圆心作直线的垂线,再证圆心到直线的距离等于半径.简记“无交点,作垂直,证半径”.
证明切线时辅助线的添加方法
图1
图2
知识讲解
随 堂 小 测
状元成才
1. 判断下列命题是否正确.
(1) 经过半径外端的直线是圆的切线. ( )
(2) 垂直于半径的直线是圆的切线. ( )
(3) 过直径的端点并且垂直于这条直径的直线是圆的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5) 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
2. 如图所示,A 是 ☉O 上一点,且 AO = 5,PO = 13,AP = 12,则 PA 与 ☉O 的位置关系是 .
A
P
O
相切
3.如图,AB是☉O的直径,∠B=∠CAD. 求证:AC是☉O的切线.
证明:∵AB是☉O 的直径,
∴∠BDA=90°,
∴∠B+∠BAD=90°.
又∵∠B=∠CAD,
∴∠CAD+∠BAD=∠BAC=90°.
∵AC 过点 A,∴ AC 是 ☉O 的切线.
4.如图,点 D 在☉O的直径 AB 的延长线上,点 C 在☉O 上,AC=CD,∠D = 30°. 求证:CD 是☉O 的切线.
解:如图,连接 OC.
∵AC = CD,∠D = 30°,∴∠A = ∠D = 30°.
∵OA = OC,
∴∠ACO =∠A = 30°,∴∠COD = 60°,
∴∠OCD = 90°,即 OC⊥CD,
∴CD 是 ☉O 的切线.
点在圆上,连半径,证垂直
5.如图,△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与☉O 相切于点 D. 求证:AC 是☉O 的切线.
证明:如图,作OE⊥AC于E,连接OD,
.
O
A
D
B
C
无切点,作垂直,证半径,
E
∴∠OEC = 90°.
∵AB是☉O的切线,∴OD⊥AB.
∴∠ODB = 90°= ∠OEC.
∵AB = AC,∴∠B = ∠C.
∵O是BC的中点,∴OB = OC .
∴△OBD ≌ △OCE(AAS),∴OD = OE,∴AC与☉O相切.
小结
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,
我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r )时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
O
O
证明切线时常用的辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
第2章 圆
2.5.2 圆的切线
第1课时 切线的判定
2.5 直线与圆的位置关系
1.探索切线与过切点的半径的关系,理解切线的判定定理.(重难点)
2.运用切线的判定定理,用三角尺过圆上一点画圆的切线.
学习目标
知识回顾
直线与圆的位置关系
定义
性质
判定
相离、相切、相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d
1个:相切
2个:相交
d>r:相离
d=r:相切
d
相切:1个
相交:2个
课时导入
观察
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中,我们常常看到切线的实例,如何判断一条直线是否为圆的切线呢?
探究
如图,OA 是☉O 的半径,经过 OA 的外端点 A,作一条直线 l ⊥ OA,圆心 O 到直线 l 的距离是多少?直线 l 和☉O 有怎样的位置关系?
l
圆心 O 到直线 l 的
距离等于半径 OA.
由圆的切线定义可知直线 l 与☉O 相切.
l
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为☉O 的半径
BC ⊥ OA 于 A
BC 为☉O 的切线
A
B
C
切线的判定定理
O
知识讲解
!在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
用三角尺过圆上一点画圆的切线.
(2) 过点 P 沿着三角尺的另一条直角边画直线 l,
则 l 就是所要画的切线.如图.
已知☉O 上一点 P,过点 P 画☉O 的切线.
画法:(1) 连接 OP,将三角尺的直角顶点放在点 P 处,
并使一直角边与半径 OP 重合;
为什么画出来的直线l 是☉O 的切线呢?
做一做
例
如图,已知 AD 是☉O 的直径,直线 BC 经过点 D,并且 AB = AC ,∠BAD =∠CAD. 求证:直线 BC 是☉O 的切线.
D
证明:∵ AB = AC,∠BAD = ∠CAD,
∴ AD ⊥ BC.
又∵ OD 是☉O 的半径,且 BC 经过点 D,
∴ 直线 BC 是☉O 的切线.
(1)已明确直线和圆有公共点,连接圆心和公共点,即半径,再证直线与半径垂直.简记“有交点,连半径,证垂直”;
(2)不明确直线和圆有无公共点,先过圆心作直线的垂线,再证圆心到直线的距离等于半径.简记“无交点,作垂直,证半径”.
证明切线时辅助线的添加方法
图1
图2
知识讲解
随 堂 小 测
状元成才
1. 判断下列命题是否正确.
(1) 经过半径外端的直线是圆的切线. ( )
(2) 垂直于半径的直线是圆的切线. ( )
(3) 过直径的端点并且垂直于这条直径的直线是圆的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5) 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
2. 如图所示,A 是 ☉O 上一点,且 AO = 5,PO = 13,AP = 12,则 PA 与 ☉O 的位置关系是 .
A
P
O
相切
3.如图,AB是☉O的直径,∠B=∠CAD. 求证:AC是☉O的切线.
证明:∵AB是☉O 的直径,
∴∠BDA=90°,
∴∠B+∠BAD=90°.
又∵∠B=∠CAD,
∴∠CAD+∠BAD=∠BAC=90°.
∵AC 过点 A,∴ AC 是 ☉O 的切线.
4.如图,点 D 在☉O的直径 AB 的延长线上,点 C 在☉O 上,AC=CD,∠D = 30°. 求证:CD 是☉O 的切线.
解:如图,连接 OC.
∵AC = CD,∠D = 30°,∴∠A = ∠D = 30°.
∵OA = OC,
∴∠ACO =∠A = 30°,∴∠COD = 60°,
∴∠OCD = 90°,即 OC⊥CD,
∴CD 是 ☉O 的切线.
点在圆上,连半径,证垂直
5.如图,△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与☉O 相切于点 D. 求证:AC 是☉O 的切线.
证明:如图,作OE⊥AC于E,连接OD,
.
O
A
D
B
C
无切点,作垂直,证半径,
E
∴∠OEC = 90°.
∵AB是☉O的切线,∴OD⊥AB.
∴∠ODB = 90°= ∠OEC.
∵AB = AC,∴∠B = ∠C.
∵O是BC的中点,∴OB = OC .
∴△OBD ≌ △OCE(AAS),∴OD = OE,∴AC与☉O相切.
小结
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,
我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r )时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
O
O
证明切线时常用的辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
