2.5 直线与圆的位置关系 2.5.2 圆的切线 第2课时 切线的性质 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.5 直线与圆的位置关系 2.5.2 圆的切线 第2课时 切线的性质 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 434.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 21:10:27 | ||
图片预览




文档简介
(共21张PPT)
第2章 圆
2.5.2 圆的切线
第2课时 切线的性质
2.5 直线与圆的位置关系
1.理解切线的性质定理的证明过程.
2.区分切线的判定定理和性质定理,并能灵活运用.
学习目标
重难点:切线的性质定理的证明过程及其应用.
知识回顾
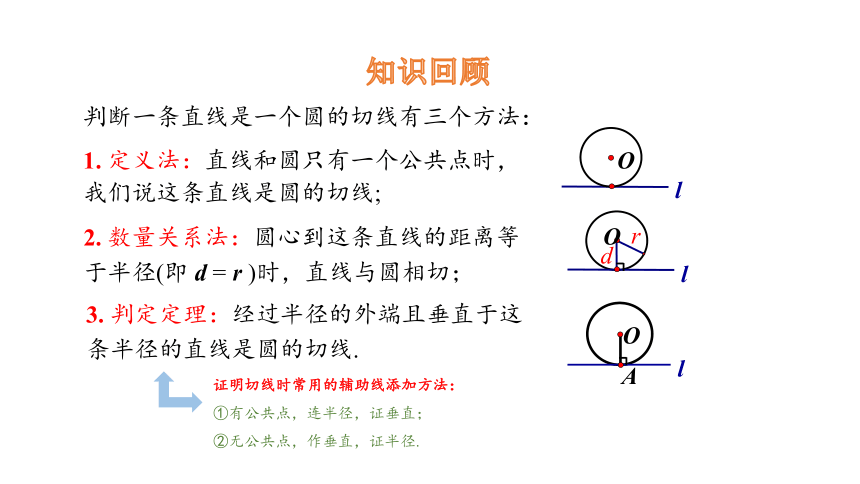
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,
我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r )时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
O
O
证明切线时常用的辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
课时导入
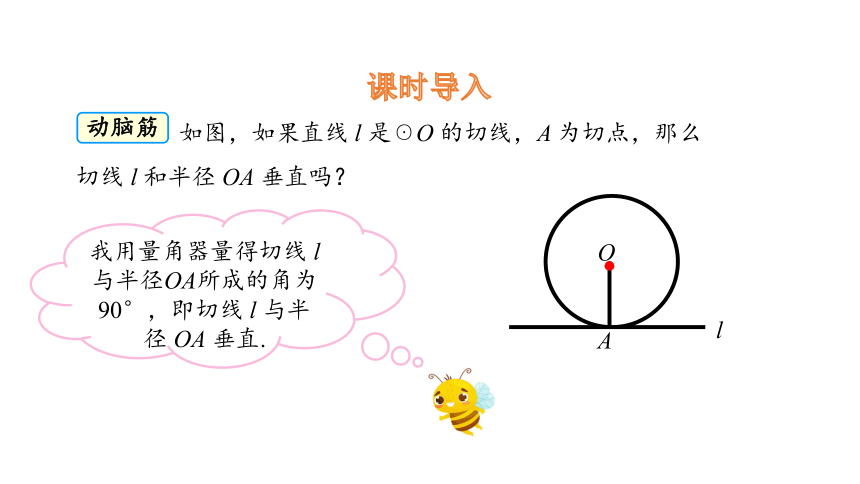
动脑筋
如图,如果直线 l 是☉O 的切线,A 为切点,那么切线 l 和半径 OA 垂直吗?
A
l
O
我用量角器量得切线 l 与半径OA所成的角为 90°,即切线 l 与半径 OA 垂直.
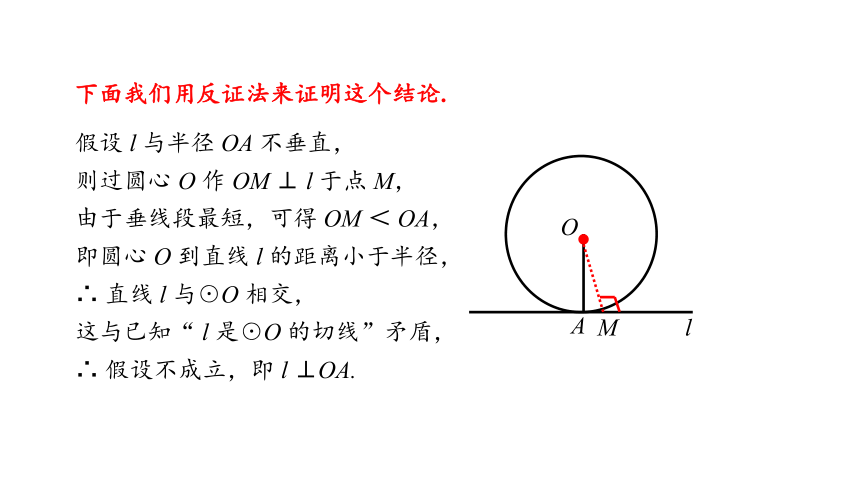
下面我们用反证法来证明这个结论.
假设 l 与半径 OA 不垂直,
则过圆心 O 作 OM ⊥ l 于点 M,
由于垂线段最短,可得 OM < OA,
即圆心 O 到直线 l 的距离小于半径,
∴ 直线 l 与☉O 相交,
这与已知“ l 是☉O 的切线”矛盾,
∴ 假设不成立,即 l ⊥OA.
M
A
l
O
知识讲解
A
l
O
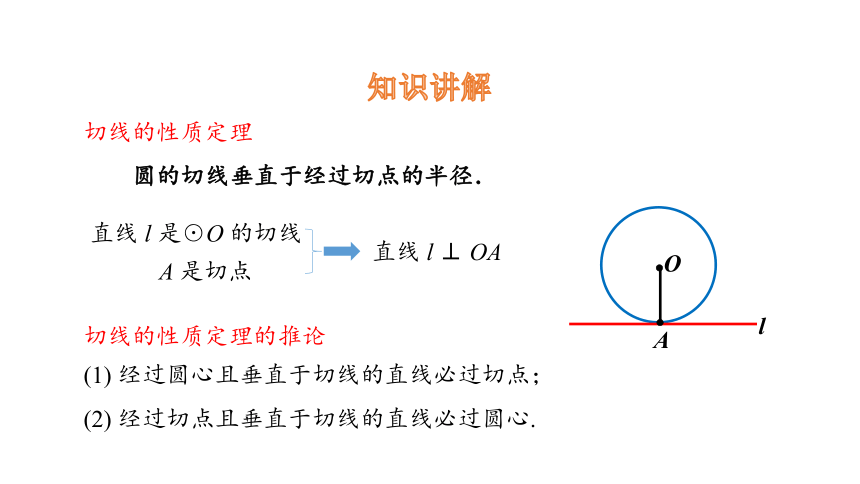
切线的性质定理
圆的切线垂直于经过切点的半径.
直线 l 是☉O 的切线
A 是切点
直线 l ⊥ OA
切线的性质定理的推论
(1) 经过圆心且垂直于切线的直线必过切点;
(2) 经过切点且垂直于切线的直线必过圆心.
例 1
如图,AB 为☉O 的直径,C 为☉O 上一点,AD 和过 C 点的切线互相垂直,垂足为 D.
求证:AC 平分 ∠DAB.
证明:连接 OC,如图.
∴OC⊥CD.
又∵ AD⊥CD,
∴ OC // AD,∴ ∠ACO = ∠CAD.
∵ OC = OA,
∴ ∠CAO = ∠ACO.
∴ ∠CAD = ∠CAO,
故 AC 平分∠DAB.
∵CD 是☉O 的切线,
A
B
O
C
D
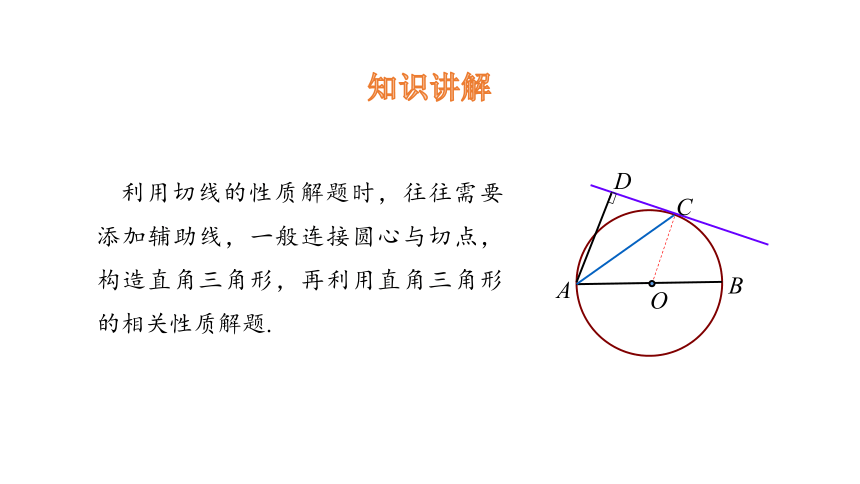
利用切线的性质解题时,往往需要添加辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
A
B
O
C
D
知识讲解
l1
O
B
A
l2
证明:经过直径两端点的切线互相平行.
已知:如图,AB 是☉O 的直径,l1,l2 分别是经过点 A,B 的切线.
求证:l1 // l2.
证明:∵OA 是☉O 的半径,l1 是过点 A 的切线,
∴ l1 ⊥ OA.
同理 l2⊥ OB,
∴ l1 ⊥ AB,且 l2⊥ AB.
∴ l1 // l2 .
例 2
随 堂 小 测
1.如图,AB 是☉O 的直径,BC 与☉O 相切于点 B,AC 交☉O 于点 D,若 ∠ACB = 50°,则 ∠BOD 等于( )
A.40° B.50° C.60° D.80°
D
解:∵BC是☉O的切线,∴∠ABC = 90°,
∴∠A = 90°-∠ACB = 90°-50°= 40°.
由圆周角定理,得∠BOD = 2∠A = 80°.
2.如图,AB 是☉O 的直径,MN 是☉O的切线,切点为N,如果∠MNB = 52°,那么 ∠NOA 的度数为( )
A
A.76° B.56°
C.54° D.52°
解:∵ MN 是☉O 的切线,
∴ ON⊥NM,∴ ∠ONM = 90°,
∴ ∠ONB = 90°-∠MNB = 90°-52°= 38°.
∵ ON = OB,
∴ ∠B = ∠ONB = 38°,
∴ ∠NOA = 2∠B = 76°.
有切线,用性质
3.如图,AB 是☉O 的直径,CD 是☉O 的切线,切点为 D,CD 与 AB 的延长线交于点 C,∠A = 30°,给出下面三个结论:
① AD = CD;② BD = BC;③ AB = 2BC.
其中正确结论的个数是( )
A.3 B.2
C.1 D.0
A
4.如图,AB 与☉O 切于点 C,OA=OB,若☉O 的半径为 8 cm,AB = 10 cm,则 OA 的长为 cm.
5.如图,在 Rt△AOB 中,OA = OB = 3,☉O 的半径为1,点 P是 AB 边上的动点,过点 P 作☉O 的一条切线 PQ (点 Q 为切点),则切线 PQ 的最小值为 .
解:如图,连接 OP,OQ.
∵ PQ 是☉O 的切线,∴ OQ⊥PQ.
∵ PQ2 = OP2 - OQ2,
∴ 当 PO⊥AB 时,线段 PQ 最短.
∵ 在 Rt△AOB 中,OA = OB = 3,
∴ AB = OA = 6,∴ OP = 3,
∴ PQ = = 2.
6.如图,☉O 切 PB 于点 B,PB = 4,PA = 2,求☉O 的半径.
O
P
B
A
解:连接 OB,则 ∠OBP = 90°.
设☉O 的半径为 r,则 OA = OB = r,OP = OA + PA = 2 + r.
在 Rt△OBP 中,
OB2 + PB2 = PO2,
解得 r = 3,
即☉O 的半径为 3.
即r2 + 42 = (2 + r)2.
7.如图,四边形 OABC 是平行四边形,以点 O 为圆心,OC 为半径的☉O 与 AB 相切于点 B,与 AO 相交于点 D,AO 的延长线交☉O 于点 E,连接 EB 交 OC 于点 F,求 ∠C 和 ∠E 的度数.
解:如图,连接 OB.
∵☉O 与 AB 相切于点 B,∴ OB⊥AB.
∵四边形 ABCO 为平行四边形,
∴ AB//OC,OA//BC,∴ OB⊥OC,∴ ∠BOC=90°.
∵ OB=OC,∴ △OCB 为等腰直角三角形,∴ ∠C = ∠OBC = 45°.
∵ AO//BC,∴ ∠AOB = ∠OBC = 45°,∴ ∠E = 22.5°.
8.如图,AB 是☉O 的直径,AC 是弦,∠BAC 的平分线 AD 交☉O 于点 D,DE 是☉O 的切线,交 AC 的延长线于点 E.
求证:DE⊥AC.
证明:如图,连接 OD.
∵ AD 是 ∠BAC 的平分线,∴ ∠EAD = ∠DAO.
又∵ OA=OD,∴ ∠DAO = ∠ODA.
∴ ∠ODA = ∠EAD,∴ OD//AC.
又∵ DE 是☉O 的切线,∴ ∠ODE = 90°,
∴ ∠E=90°,即 DE⊥AC.
9.如图,PA 为☉O 的切线,A 为切点.直线 PO 与☉O 交于 B、C 两点,∠P = 30°,连接 AO、AB、AC.
(1)求证:△ACB ≌ △APO;
(2)若 AP = ,求☉O 的半径.
O
A
B
P
C
(1)求证:△ACB ≌ △APO;
在 △ACB 和 △APO 中,
∠BAC = ∠OAP,AB = AO,∠ABO = ∠AOB,
∴ △ACB ≌ △APO.
(1)证明:∵ PA 为☉O 的切线,A 为切点,
又∵ ∠P = 30°,∴ ∠AOB = 60°,
又∵ OA = OB,∴ △AOB 为等边三角形,
∴ AB = AO,∠ABO = 60°.
又∵ BC 为☉O 的直径,∴ ∠BAC = 90°.
∴ ∠OAP = 90°.
O
A
B
P
C
(2)若AP = ,求☉O 的半径.
∴ AO = 1,
∴ CB = OP = 2,
∴ OB = 1,即☉O 的半径为 1.
(2)解:在 Rt△AOP 中,∠P = 30°,AP = ,
O
A
B
P
C
小结
切线的
性质
有1个公共点
d=r
圆的切线垂直于经过切点的半径
有切线时常用辅助线的添加方法:
见切线,连切点,得垂直.
性质定理
第2章 圆
2.5.2 圆的切线
第2课时 切线的性质
2.5 直线与圆的位置关系
1.理解切线的性质定理的证明过程.
2.区分切线的判定定理和性质定理,并能灵活运用.
学习目标
重难点:切线的性质定理的证明过程及其应用.
知识回顾
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,
我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r )时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
O
O
证明切线时常用的辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
课时导入
动脑筋
如图,如果直线 l 是☉O 的切线,A 为切点,那么切线 l 和半径 OA 垂直吗?
A
l
O
我用量角器量得切线 l 与半径OA所成的角为 90°,即切线 l 与半径 OA 垂直.
下面我们用反证法来证明这个结论.
假设 l 与半径 OA 不垂直,
则过圆心 O 作 OM ⊥ l 于点 M,
由于垂线段最短,可得 OM < OA,
即圆心 O 到直线 l 的距离小于半径,
∴ 直线 l 与☉O 相交,
这与已知“ l 是☉O 的切线”矛盾,
∴ 假设不成立,即 l ⊥OA.
M
A
l
O
知识讲解
A
l
O
切线的性质定理
圆的切线垂直于经过切点的半径.
直线 l 是☉O 的切线
A 是切点
直线 l ⊥ OA
切线的性质定理的推论
(1) 经过圆心且垂直于切线的直线必过切点;
(2) 经过切点且垂直于切线的直线必过圆心.
例 1
如图,AB 为☉O 的直径,C 为☉O 上一点,AD 和过 C 点的切线互相垂直,垂足为 D.
求证:AC 平分 ∠DAB.
证明:连接 OC,如图.
∴OC⊥CD.
又∵ AD⊥CD,
∴ OC // AD,∴ ∠ACO = ∠CAD.
∵ OC = OA,
∴ ∠CAO = ∠ACO.
∴ ∠CAD = ∠CAO,
故 AC 平分∠DAB.
∵CD 是☉O 的切线,
A
B
O
C
D
利用切线的性质解题时,往往需要添加辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
A
B
O
C
D
知识讲解
l1
O
B
A
l2
证明:经过直径两端点的切线互相平行.
已知:如图,AB 是☉O 的直径,l1,l2 分别是经过点 A,B 的切线.
求证:l1 // l2.
证明:∵OA 是☉O 的半径,l1 是过点 A 的切线,
∴ l1 ⊥ OA.
同理 l2⊥ OB,
∴ l1 ⊥ AB,且 l2⊥ AB.
∴ l1 // l2 .
例 2
随 堂 小 测
1.如图,AB 是☉O 的直径,BC 与☉O 相切于点 B,AC 交☉O 于点 D,若 ∠ACB = 50°,则 ∠BOD 等于( )
A.40° B.50° C.60° D.80°
D
解:∵BC是☉O的切线,∴∠ABC = 90°,
∴∠A = 90°-∠ACB = 90°-50°= 40°.
由圆周角定理,得∠BOD = 2∠A = 80°.
2.如图,AB 是☉O 的直径,MN 是☉O的切线,切点为N,如果∠MNB = 52°,那么 ∠NOA 的度数为( )
A
A.76° B.56°
C.54° D.52°
解:∵ MN 是☉O 的切线,
∴ ON⊥NM,∴ ∠ONM = 90°,
∴ ∠ONB = 90°-∠MNB = 90°-52°= 38°.
∵ ON = OB,
∴ ∠B = ∠ONB = 38°,
∴ ∠NOA = 2∠B = 76°.
有切线,用性质
3.如图,AB 是☉O 的直径,CD 是☉O 的切线,切点为 D,CD 与 AB 的延长线交于点 C,∠A = 30°,给出下面三个结论:
① AD = CD;② BD = BC;③ AB = 2BC.
其中正确结论的个数是( )
A.3 B.2
C.1 D.0
A
4.如图,AB 与☉O 切于点 C,OA=OB,若☉O 的半径为 8 cm,AB = 10 cm,则 OA 的长为 cm.
5.如图,在 Rt△AOB 中,OA = OB = 3,☉O 的半径为1,点 P是 AB 边上的动点,过点 P 作☉O 的一条切线 PQ (点 Q 为切点),则切线 PQ 的最小值为 .
解:如图,连接 OP,OQ.
∵ PQ 是☉O 的切线,∴ OQ⊥PQ.
∵ PQ2 = OP2 - OQ2,
∴ 当 PO⊥AB 时,线段 PQ 最短.
∵ 在 Rt△AOB 中,OA = OB = 3,
∴ AB = OA = 6,∴ OP = 3,
∴ PQ = = 2.
6.如图,☉O 切 PB 于点 B,PB = 4,PA = 2,求☉O 的半径.
O
P
B
A
解:连接 OB,则 ∠OBP = 90°.
设☉O 的半径为 r,则 OA = OB = r,OP = OA + PA = 2 + r.
在 Rt△OBP 中,
OB2 + PB2 = PO2,
解得 r = 3,
即☉O 的半径为 3.
即r2 + 42 = (2 + r)2.
7.如图,四边形 OABC 是平行四边形,以点 O 为圆心,OC 为半径的☉O 与 AB 相切于点 B,与 AO 相交于点 D,AO 的延长线交☉O 于点 E,连接 EB 交 OC 于点 F,求 ∠C 和 ∠E 的度数.
解:如图,连接 OB.
∵☉O 与 AB 相切于点 B,∴ OB⊥AB.
∵四边形 ABCO 为平行四边形,
∴ AB//OC,OA//BC,∴ OB⊥OC,∴ ∠BOC=90°.
∵ OB=OC,∴ △OCB 为等腰直角三角形,∴ ∠C = ∠OBC = 45°.
∵ AO//BC,∴ ∠AOB = ∠OBC = 45°,∴ ∠E = 22.5°.
8.如图,AB 是☉O 的直径,AC 是弦,∠BAC 的平分线 AD 交☉O 于点 D,DE 是☉O 的切线,交 AC 的延长线于点 E.
求证:DE⊥AC.
证明:如图,连接 OD.
∵ AD 是 ∠BAC 的平分线,∴ ∠EAD = ∠DAO.
又∵ OA=OD,∴ ∠DAO = ∠ODA.
∴ ∠ODA = ∠EAD,∴ OD//AC.
又∵ DE 是☉O 的切线,∴ ∠ODE = 90°,
∴ ∠E=90°,即 DE⊥AC.
9.如图,PA 为☉O 的切线,A 为切点.直线 PO 与☉O 交于 B、C 两点,∠P = 30°,连接 AO、AB、AC.
(1)求证:△ACB ≌ △APO;
(2)若 AP = ,求☉O 的半径.
O
A
B
P
C
(1)求证:△ACB ≌ △APO;
在 △ACB 和 △APO 中,
∠BAC = ∠OAP,AB = AO,∠ABO = ∠AOB,
∴ △ACB ≌ △APO.
(1)证明:∵ PA 为☉O 的切线,A 为切点,
又∵ ∠P = 30°,∴ ∠AOB = 60°,
又∵ OA = OB,∴ △AOB 为等边三角形,
∴ AB = AO,∠ABO = 60°.
又∵ BC 为☉O 的直径,∴ ∠BAC = 90°.
∴ ∠OAP = 90°.
O
A
B
P
C
(2)若AP = ,求☉O 的半径.
∴ AO = 1,
∴ CB = OP = 2,
∴ OB = 1,即☉O 的半径为 1.
(2)解:在 Rt△AOP 中,∠P = 30°,AP = ,
O
A
B
P
C
小结
切线的
性质
有1个公共点
d=r
圆的切线垂直于经过切点的半径
有切线时常用辅助线的添加方法:
见切线,连切点,得垂直.
性质定理
