2.5.3 切线长定理 课件(共23张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.5.3 切线长定理 课件(共23张PPT) 2023-2024学年数学湘教版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 699.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 11:19:28 | ||
图片预览







文档简介
(共23张PPT)
第2章 圆
2.5.3 切线长定理
2.5 直线与圆的位置关系
1.了解切线长的概念.(重点)
2.探索并证明切线长定理.(重难点)
3.切线长定理的简单应用.
学习目标
课时导入
我们学习了过圆上一点作已知圆的切线(如左图所示),如果点 P 是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
P
O
B
A
O.
P
A
B
知识讲解
P
1. 切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2. 切线长与切线的区别在哪里?
探究
B
P
O
A
在透明纸上画出下图,设 PA,PB 是☉O 的两条切线,A、B 是切点,沿直线 OP 将图形对折,你能猜测一下 PA 与 PB,∠APO 与 ∠BPO 分别有什么关系吗?
(利用图形轴对称性解释)
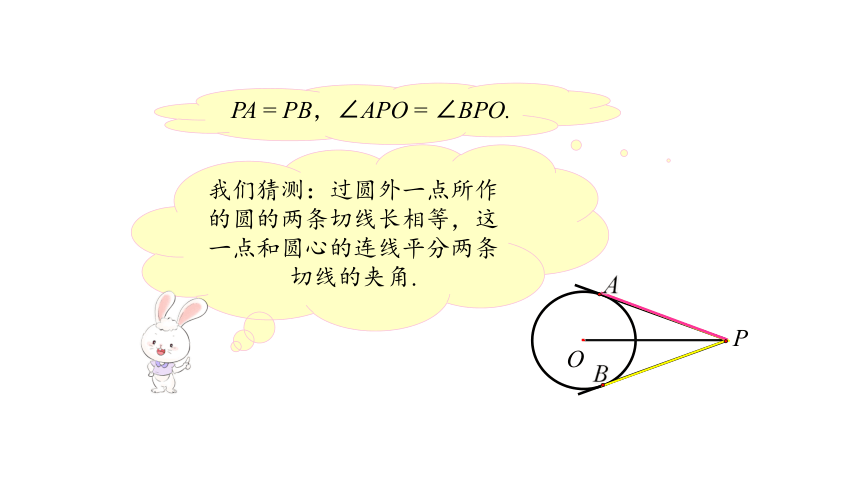
PA = PB,∠APO = ∠BPO.
B
P
O
A
我们猜测:过圆外一点所作的圆的两条切线长相等,这一点和圆心的连线平分两条切线的夹角.
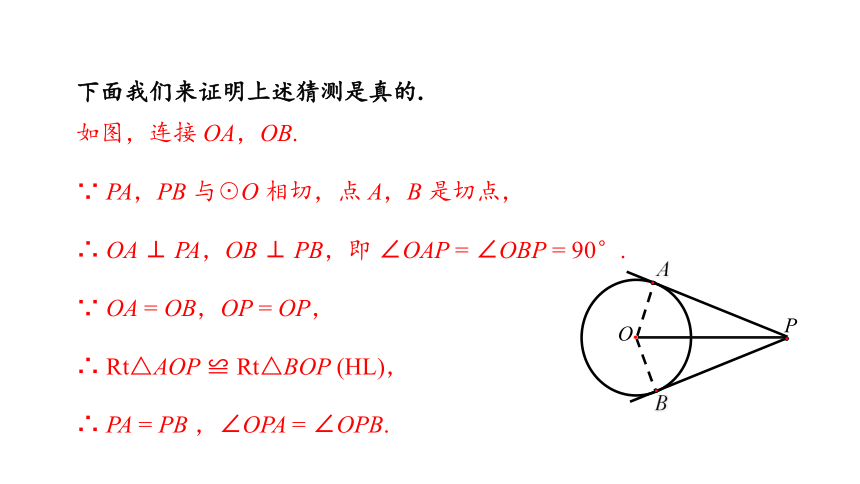
如图,连接 OA,OB.
∵ PA,PB 与☉O 相切,点 A,B 是切点,
∴ OA ⊥ PA,OB ⊥ PB,即 ∠OAP = ∠OBP = 90°.
∵ OA = OB,OP = OP,
∴ Rt△AOP ≌ Rt△BOP (HL),
∴ PA = PB ,∠OPA = ∠OPB.
B
P
O
A
下面我们来证明上述猜测是真的.
知识讲解
切线长定理:
过圆外一点所作的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
PA、PB 分别切☉O 于 A、B
PA = PB
∠OPA = ∠OPB
B
P
O
A
切线长定理为证明线段相等、角相等提供了新的方法.
例
如图,AD 是☉O 的直径,点 C 为☉O 外一点,CA 和 CB 是☉O 的切线,A 和 B 是切点,连接 BD.
求证:CO//BD.
分析:连接 AB,因为 AD 为直径,那么∠ABD = 90°,即 BD⊥AB. 因此要证 CO//BD,只要证 CO⊥AB 即可.
证明:如图,连接 AB.
∵CA、CB 是☉O 的切线,点 A、B 是切点,
∴CA = CB,∠ACO = ∠BCO,
∴CO⊥AB.
∵AD 是☉O 的直径,
∴∠ABD = 90°,
即BD⊥AB,
∴CO//BD.
特别提醒
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段相等.
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
知识讲解
随 堂 小 测
1.如图,直线 AB,AD 分别与☉O 相切于点 B,D,C 为☉O
上一点, 且 ∠ BCD = 130°,则 ∠A 的度数是( )
A.70°
B.85°
C.80°
D.100°
C
2.如图,已知四边形 ABCD 的每条边都和☉O 相切,且 BC = 10,AD = 7,则四边形 ABCD 的周长为( )
A.32 B.34 C.36 D.38
B
解:设四边形的各边与圆的切点分别为 P,Q,M,N,
则 AQ = AM,BN = BM,CN = CP,DP = DQ,
所以四边形 ABCD 的两组对边的和相等,
所以四边形 ABCD 的周长 = 2×(7+10) = 34.
P
Q
M
N
D
C
A
B
3.如图,菱形 ABCD 的边长为 10,圆 O 分别与 AB、AD 相切于 E、F 两点,且与 BG 相切于 G 点.若 AO = 5,且圆 O 的半径为 3,则 BG 的长为( )
A.4 B.5 C.6 D.7
解:如图,连接 OE.
∵☉O 与 AB相切于 E,∴ ∠AEO = 90°,
∵AO = 5,OE = 3,
∵AB = 10,∴BE = 6.
∵BG 与☉O 相切于 G,∴BG = BE = 6.
C
B
P
O
A
4. PA、PB 是☉O 的两条切线,A,B 是切点,OA = 3.
(1)若AP = 4,则OP = ;
(2)若∠BPA = 60°,则 OP = .
5
6
5.如图,PA,PB 切☉O 于 A,B 两点,CD 切☉O 于点 E,交 PA,
PB 于点 C,D. 若☉O 的半径为 2,△PCD 的周长等于 4,则
线段 AB 的长是_____ .
6.如图,AB,BC,CD 分别与☉O 相切于点 E,F,G,
若∠BOC = 90°,求证:AB//CD.
证明:∵∠BOC = 90°,∴∠OBC+∠OCB = 90°.
又∵ BE 与 BF 为☉O 的切线,
∴ BO 为 ∠EBF 的平分线.∴ ∠OBE = ∠OBC.
同理可得 ∠OCB = ∠OCG.
∴ ∠OBE+∠OCG = ∠OBC+∠OCB = 90°,
∴ ∠OBC+∠OCB+∠OBE+∠OCG = 180°,
即 ∠ABF+∠DCF = 180°,∴AB//CD.
7.如图,PA、PB 是☉O 的切线,A、B 为切点,AC 是☉O 的直径,∠BAC = 25°,求∠P 的度数.
解:由切线长定理可知 PA = PB.
∵ PA 是☉O 的切线.
∴ ∠OAP = 90°.
∵ ∠BAC = 25°,∴ ∠BAP = 65°.
又∵ PA = PB,∴ ∠BAP = ∠ABP = 65°,
∴ ∠P = 180°-∠BAP-∠ABP = 50°.
8.如图,一个油桶靠在墙边,量得WY = 1.65 m,并且 XY⊥WY,这个油桶底面半径是多少
解:设圆心为 O,连接 OW,OX.
∵ YW,YX 均是☉O 的切线,∴ OW⊥WY,OX⊥XY.
又∵ XY⊥WY,∴∠OWY = ∠OXY = ∠WYX = 90°,
∴ 四边形 OWYX 是矩形,
又∵ OW = OX,∴四边形 OWYX 是正方形,∴ OW = WY = 1.65 m,
即这个油桶底面半径是1.65 m.
9.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为 30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得 PA = 5 cm,求铁环的半径.
分析:欲求半径 OP,取圆的圆心为 O,连接 OA,OP,由切线性质知 △OPA 为直角三角形,从而在 Rt△OPA 中由勾股定理易求得半径.
O
在 Rt△OPA 中,PA = 5,∠POA = 30°,
O
Q
解:过 O 作 OQ⊥AB 于 Q,设铁环的圆心为 O,连接 OP、OA.
∵AP、AQ 为☉O 的切线,
∴AO 为∠PAQ 的平分线,即∠PAO = ∠QAO.
又∠BAC = 60°,∠PAO+∠QAO+∠BAC = 180°,∴∠PAO = ∠QAO = 60°.
即铁环的半径为
小结
切线长
切线长定理
作用
过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
内容
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
经过圆外一点作圆的切线,这点和切点
之间的线段的长.
第2章 圆
2.5.3 切线长定理
2.5 直线与圆的位置关系
1.了解切线长的概念.(重点)
2.探索并证明切线长定理.(重难点)
3.切线长定理的简单应用.
学习目标
课时导入
我们学习了过圆上一点作已知圆的切线(如左图所示),如果点 P 是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
P
O
B
A
O.
P
A
B
知识讲解
P
1. 切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2. 切线长与切线的区别在哪里?
探究
B
P
O
A
在透明纸上画出下图,设 PA,PB 是☉O 的两条切线,A、B 是切点,沿直线 OP 将图形对折,你能猜测一下 PA 与 PB,∠APO 与 ∠BPO 分别有什么关系吗?
(利用图形轴对称性解释)
PA = PB,∠APO = ∠BPO.
B
P
O
A
我们猜测:过圆外一点所作的圆的两条切线长相等,这一点和圆心的连线平分两条切线的夹角.
如图,连接 OA,OB.
∵ PA,PB 与☉O 相切,点 A,B 是切点,
∴ OA ⊥ PA,OB ⊥ PB,即 ∠OAP = ∠OBP = 90°.
∵ OA = OB,OP = OP,
∴ Rt△AOP ≌ Rt△BOP (HL),
∴ PA = PB ,∠OPA = ∠OPB.
B
P
O
A
下面我们来证明上述猜测是真的.
知识讲解
切线长定理:
过圆外一点所作的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
PA、PB 分别切☉O 于 A、B
PA = PB
∠OPA = ∠OPB
B
P
O
A
切线长定理为证明线段相等、角相等提供了新的方法.
例
如图,AD 是☉O 的直径,点 C 为☉O 外一点,CA 和 CB 是☉O 的切线,A 和 B 是切点,连接 BD.
求证:CO//BD.
分析:连接 AB,因为 AD 为直径,那么∠ABD = 90°,即 BD⊥AB. 因此要证 CO//BD,只要证 CO⊥AB 即可.
证明:如图,连接 AB.
∵CA、CB 是☉O 的切线,点 A、B 是切点,
∴CA = CB,∠ACO = ∠BCO,
∴CO⊥AB.
∵AD 是☉O 的直径,
∴∠ABD = 90°,
即BD⊥AB,
∴CO//BD.
特别提醒
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段相等.
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
知识讲解
随 堂 小 测
1.如图,直线 AB,AD 分别与☉O 相切于点 B,D,C 为☉O
上一点, 且 ∠ BCD = 130°,则 ∠A 的度数是( )
A.70°
B.85°
C.80°
D.100°
C
2.如图,已知四边形 ABCD 的每条边都和☉O 相切,且 BC = 10,AD = 7,则四边形 ABCD 的周长为( )
A.32 B.34 C.36 D.38
B
解:设四边形的各边与圆的切点分别为 P,Q,M,N,
则 AQ = AM,BN = BM,CN = CP,DP = DQ,
所以四边形 ABCD 的两组对边的和相等,
所以四边形 ABCD 的周长 = 2×(7+10) = 34.
P
Q
M
N
D
C
A
B
3.如图,菱形 ABCD 的边长为 10,圆 O 分别与 AB、AD 相切于 E、F 两点,且与 BG 相切于 G 点.若 AO = 5,且圆 O 的半径为 3,则 BG 的长为( )
A.4 B.5 C.6 D.7
解:如图,连接 OE.
∵☉O 与 AB相切于 E,∴ ∠AEO = 90°,
∵AO = 5,OE = 3,
∵AB = 10,∴BE = 6.
∵BG 与☉O 相切于 G,∴BG = BE = 6.
C
B
P
O
A
4. PA、PB 是☉O 的两条切线,A,B 是切点,OA = 3.
(1)若AP = 4,则OP = ;
(2)若∠BPA = 60°,则 OP = .
5
6
5.如图,PA,PB 切☉O 于 A,B 两点,CD 切☉O 于点 E,交 PA,
PB 于点 C,D. 若☉O 的半径为 2,△PCD 的周长等于 4,则
线段 AB 的长是_____ .
6.如图,AB,BC,CD 分别与☉O 相切于点 E,F,G,
若∠BOC = 90°,求证:AB//CD.
证明:∵∠BOC = 90°,∴∠OBC+∠OCB = 90°.
又∵ BE 与 BF 为☉O 的切线,
∴ BO 为 ∠EBF 的平分线.∴ ∠OBE = ∠OBC.
同理可得 ∠OCB = ∠OCG.
∴ ∠OBE+∠OCG = ∠OBC+∠OCB = 90°,
∴ ∠OBC+∠OCB+∠OBE+∠OCG = 180°,
即 ∠ABF+∠DCF = 180°,∴AB//CD.
7.如图,PA、PB 是☉O 的切线,A、B 为切点,AC 是☉O 的直径,∠BAC = 25°,求∠P 的度数.
解:由切线长定理可知 PA = PB.
∵ PA 是☉O 的切线.
∴ ∠OAP = 90°.
∵ ∠BAC = 25°,∴ ∠BAP = 65°.
又∵ PA = PB,∴ ∠BAP = ∠ABP = 65°,
∴ ∠P = 180°-∠BAP-∠ABP = 50°.
8.如图,一个油桶靠在墙边,量得WY = 1.65 m,并且 XY⊥WY,这个油桶底面半径是多少
解:设圆心为 O,连接 OW,OX.
∵ YW,YX 均是☉O 的切线,∴ OW⊥WY,OX⊥XY.
又∵ XY⊥WY,∴∠OWY = ∠OXY = ∠WYX = 90°,
∴ 四边形 OWYX 是矩形,
又∵ OW = OX,∴四边形 OWYX 是正方形,∴ OW = WY = 1.65 m,
即这个油桶底面半径是1.65 m.
9.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为 30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得 PA = 5 cm,求铁环的半径.
分析:欲求半径 OP,取圆的圆心为 O,连接 OA,OP,由切线性质知 △OPA 为直角三角形,从而在 Rt△OPA 中由勾股定理易求得半径.
O
在 Rt△OPA 中,PA = 5,∠POA = 30°,
O
Q
解:过 O 作 OQ⊥AB 于 Q,设铁环的圆心为 O,连接 OP、OA.
∵AP、AQ 为☉O 的切线,
∴AO 为∠PAQ 的平分线,即∠PAO = ∠QAO.
又∠BAC = 60°,∠PAO+∠QAO+∠BAC = 180°,∴∠PAO = ∠QAO = 60°.
即铁环的半径为
小结
切线长
切线长定理
作用
过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
内容
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
经过圆外一点作圆的切线,这点和切点
之间的线段的长.
