2.2 圆心角、圆周角 2.2.1 圆心角 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.2 圆心角、圆周角 2.2.1 圆心角 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 448.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:29:45 | ||
图片预览








文档简介
(共21张PPT)
第2章 圆
2.2 圆心角、圆周角
2.2.1 圆心角
学习目标
1.理解圆心角的概念.
2.掌握圆心角、弧、弦之间的关系.
3.体验利用旋转变换来研究圆的性质的思想方法.
重点:圆心角定理.
难点:根据圆的旋转不变性推导出圆心角定理.
课时导入
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
知识讲解
O
A
B
M
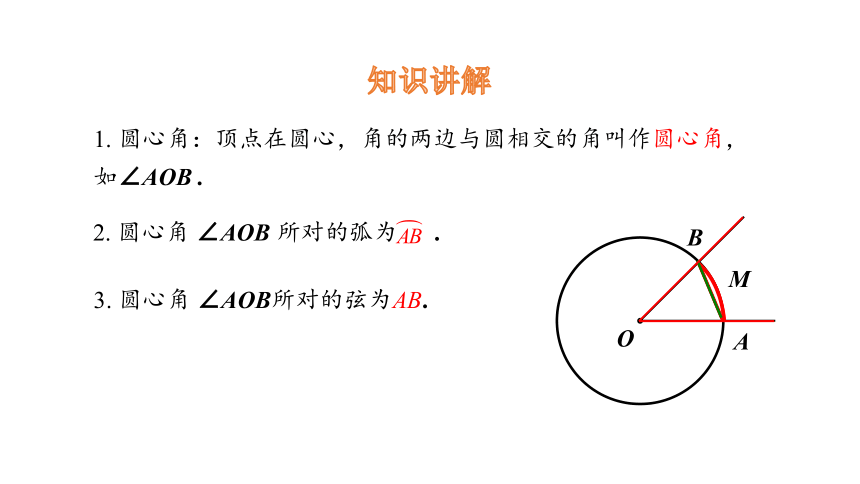
1. 圆心角:顶点在圆心,角的两边与圆相交的角叫作圆心角,如∠AOB .
3. 圆心角 ∠AOB所对的弦为AB.
2. 圆心角 ∠AOB 所对的弧为 .
活学活用
判断下列各图中的角是不是圆心角,并说明理由.
圆内角
圆外角
圆周角(后面会学到)
圆心角
在同圆中探究
C
·
O
A
B
D
因为将圆绕圆心旋转任一角度都能与自身重合,所以可将☉O 绕圆心 O 旋转,使点 A 与点 C 重合.由于∠AOB = ∠COD,因此,点 B 与点 D 重合.从而 ,AB = CD.
问题1 已知在☉O中,圆心角∠AOB = ∠COD,那么 与 ,弦 AB 与弦 CD 有怎样的数量关系?
动脑筋
问题2 如图,在等圆中,如果∠AOB = ∠CO ′D,问题1中的等量关系是否依然成立?为什么?
在等圆中探究
O ′
O
A
B
C
D
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO′D,那么, ,AB = CD.
知识讲解
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
∠AOB = ∠COD
AB = CD
A
B
O
D
C
问题3 在结论“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以去掉,原因如图所示.
A
B
O
D
C
知识讲解
在同圆或等圆中,相等的弦所对的圆心角相等,
所对的弧也相等.
A
B
O
D
C
AB = CD
∠AOB = ∠COD
知识讲解
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
知一推二
例
如图,等边三角形ABC 的顶点 A,B,C在☉O 上,求圆心角∠AOB 的度数 .
·
A
B
C
O
∴ AB = BC = AC.
∴ ∠AOB = ∠BOC = ∠COA.
解:∵△ABC 是等边三角形 ,
又∵ ∠AOB+∠BOC+∠COA = 360°,
∴ ∠AOB= (∠AOB+∠BOC+∠COA)
= 360°=120°.
随 堂 小 测
1.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
B
在同圆或等圆中
在同圆或等圆中
在同圆或等圆中
2.下面四个图中的角,是圆心角的是( )
D
3.在☉O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB >2CD
C. AB<2CD
D.不能确定
(
(
(
(
(
(
(
(
A
4.如图,AB是☉O的直径,BC=CD=DE,∠AOE=72°,则∠COD的度数是( )
A.36° B.72°
C.108° D.48°
(
A
(
(
5.如图,在☉O中,AD=BC,求证:AB=CD.
证明:∵AD=BC,
∴AD=BC,
∴AD+AC=BC+AC,
即CD=AB,
∴AB=CD.
(
(
(
(
(
(
(
(
6.如图,在☉O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
A
B
C
D
E
O
解:CD = 2AB 不成立. 理由如下:
取 的中点 E,连接 OE,CE,DE,如图,
那么∠AOB = ∠COE = ∠DOE,
所以弦AB = CE = DE.
在△CDE中,CE+DE >CD,即CD<2AB.
7.如图,在☉O中,AB=AC,∠ACB=60°.
(1)求证:∠AOB=∠BOC=∠AOC;
(2)若D是AB的中点,求证:四边形OADB是菱形.
(
(
A
B
C
O
D
(
解:(1)因为
AB=AC,
(
(
所以AB=AC.
又因为∠ACB=60° ,
所以△ABC是等边三角形,
所以AB=BC=CA,
所以∠AOB=∠BOC=∠AOC.
(2)连接OD,如图.
A
B
C
O
D
(
因为D是AB的中点,所以 AD= BD,
所以∠AOD=∠BOD=∠ACB=60°.
所以△OAD和△OBD都是等边三角形,
又因为OD=OA,OD=OB,
所以OA=AD=OD,OB=BD=OD,
所以OA=AD=DB=BO,所以四边形OADB是菱形.
小结
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
圆心角
概念:顶点在圆心的角
第2章 圆
2.2 圆心角、圆周角
2.2.1 圆心角
学习目标
1.理解圆心角的概念.
2.掌握圆心角、弧、弦之间的关系.
3.体验利用旋转变换来研究圆的性质的思想方法.
重点:圆心角定理.
难点:根据圆的旋转不变性推导出圆心角定理.
课时导入
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
知识讲解
O
A
B
M
1. 圆心角:顶点在圆心,角的两边与圆相交的角叫作圆心角,如∠AOB .
3. 圆心角 ∠AOB所对的弦为AB.
2. 圆心角 ∠AOB 所对的弧为 .
活学活用
判断下列各图中的角是不是圆心角,并说明理由.
圆内角
圆外角
圆周角(后面会学到)
圆心角
在同圆中探究
C
·
O
A
B
D
因为将圆绕圆心旋转任一角度都能与自身重合,所以可将☉O 绕圆心 O 旋转,使点 A 与点 C 重合.由于∠AOB = ∠COD,因此,点 B 与点 D 重合.从而 ,AB = CD.
问题1 已知在☉O中,圆心角∠AOB = ∠COD,那么 与 ,弦 AB 与弦 CD 有怎样的数量关系?
动脑筋
问题2 如图,在等圆中,如果∠AOB = ∠CO ′D,问题1中的等量关系是否依然成立?为什么?
在等圆中探究
O ′
O
A
B
C
D
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO′D,那么, ,AB = CD.
知识讲解
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
∠AOB = ∠COD
AB = CD
A
B
O
D
C
问题3 在结论“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以去掉,原因如图所示.
A
B
O
D
C
知识讲解
在同圆或等圆中,相等的弦所对的圆心角相等,
所对的弧也相等.
A
B
O
D
C
AB = CD
∠AOB = ∠COD
知识讲解
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
知一推二
例
如图,等边三角形ABC 的顶点 A,B,C在☉O 上,求圆心角∠AOB 的度数 .
·
A
B
C
O
∴ AB = BC = AC.
∴ ∠AOB = ∠BOC = ∠COA.
解:∵△ABC 是等边三角形 ,
又∵ ∠AOB+∠BOC+∠COA = 360°,
∴ ∠AOB= (∠AOB+∠BOC+∠COA)
= 360°=120°.
随 堂 小 测
1.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
B
在同圆或等圆中
在同圆或等圆中
在同圆或等圆中
2.下面四个图中的角,是圆心角的是( )
D
3.在☉O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB >2CD
C. AB<2CD
D.不能确定
(
(
(
(
(
(
(
(
A
4.如图,AB是☉O的直径,BC=CD=DE,∠AOE=72°,则∠COD的度数是( )
A.36° B.72°
C.108° D.48°
(
A
(
(
5.如图,在☉O中,AD=BC,求证:AB=CD.
证明:∵AD=BC,
∴AD=BC,
∴AD+AC=BC+AC,
即CD=AB,
∴AB=CD.
(
(
(
(
(
(
(
(
6.如图,在☉O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
A
B
C
D
E
O
解:CD = 2AB 不成立. 理由如下:
取 的中点 E,连接 OE,CE,DE,如图,
那么∠AOB = ∠COE = ∠DOE,
所以弦AB = CE = DE.
在△CDE中,CE+DE >CD,即CD<2AB.
7.如图,在☉O中,AB=AC,∠ACB=60°.
(1)求证:∠AOB=∠BOC=∠AOC;
(2)若D是AB的中点,求证:四边形OADB是菱形.
(
(
A
B
C
O
D
(
解:(1)因为
AB=AC,
(
(
所以AB=AC.
又因为∠ACB=60° ,
所以△ABC是等边三角形,
所以AB=BC=CA,
所以∠AOB=∠BOC=∠AOC.
(2)连接OD,如图.
A
B
C
O
D
(
因为D是AB的中点,所以 AD= BD,
所以∠AOD=∠BOD=∠ACB=60°.
所以△OAD和△OBD都是等边三角形,
又因为OD=OA,OD=OB,
所以OA=AD=OD,OB=BD=OD,
所以OA=AD=DB=BO,所以四边形OADB是菱形.
小结
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
圆心角
概念:顶点在圆心的角
