3.3 三视图 第2课时 由三视图判断几何体 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 3.3 三视图 第2课时 由三视图判断几何体 课件 (共21张PPT) 2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 23:54:50 | ||
图片预览








文档简介
(共21张PPT)
第3章 投影与视图
3.3 三视图
第2课时 由三视图判断几何体
1.会从投影角度理解视图的概念.(重点)
2.会画简单几何体的三视图.(重难点)
3.能根据三视图想象简单几何体的形状.(重难点)
4.通过观察和动手实践,体会立体图形→三视图→立体图形的转换过程,培养空间观念.
学习目标
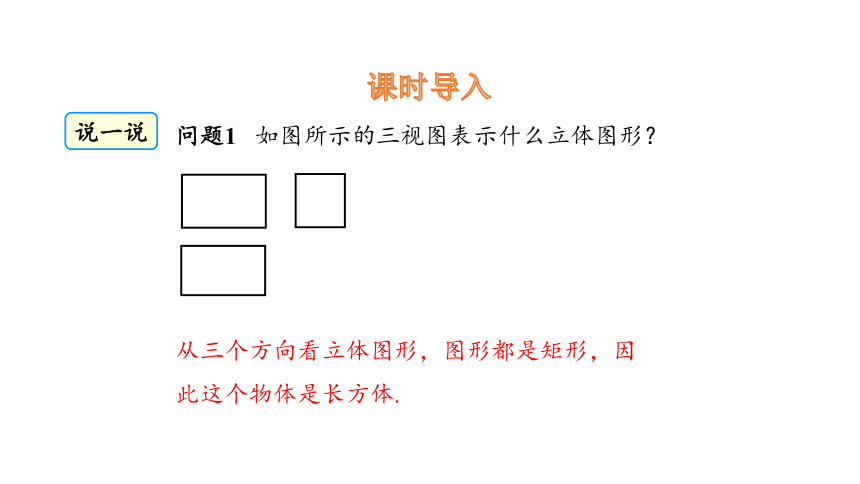
课时导入
问题1 如图所示的三视图表示什么立体图形?
从三个方向看立体图形,图形都是矩形,因此这个物体是长方体.
说一说
问题2 如图所示的三视图表示什么立体图形?
从正面,左面看立体图形,图形都是矩形,从上面看是圆形,因此这个物体是圆柱.
方法总结
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
根据图示三视图描述物体的形状?
分析:从主视图可知,物体的正面是矩形的样子,且中间有一条棱(实线)可见到;由俯视图可知,物体是矩形的样子,且中间有两条棱可见到;由左视图可知,物体的侧面是正六边形的样子.综合各视图可知,该物体是正六棱柱.
主视图
左视图
俯视图
例1
解:物体是正六棱柱,如图所示.
例2
解:这个零件由两部分构成:上面一个是圆柱、下面一个是长方体,圆柱立于长方体的中央.
如图是一个零件的三视图,试描述出这个零件的形状.
主视图
左视图
俯视图
随 堂 小 测
1.如图是某工件的三视图,其中圆的半径是 10 cm,等腰三角形的高是 30 cm,则此工件的体积是 ( )
A.1500π cm3 B.500π cm3
C.1000π cm3 D.2000π cm3
C
C
2.已知某物体的三视图如图所示,那么与它对应的物体是( )
3.一个立体图形的三视图如图所示,则这个立体图形是( )
D
4.一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,最少需用________个小正方体.
6
解:(1)此模型由两个长方体组成:上面是一个小长方体,下面是一个大长方体.
5.已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)模型的体积为10×6×5+3×1.5×2=309(m3),则该模型的质量为309×360=111 240(kg).
(2)制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少千克?
(3)模型的表面积为3×2×2+2×1.5×2+10×5×2+6×5×2+10×6×2=298(m2),
需要油漆298÷4=74.5(kg).
(3)如果要给这个模型刷油漆,每千克油漆可以刷4 m2,需要油漆多少千克?
6.请根据下面提供的三视图,画出几何图形.
(1)
主视图
左视图
俯视图
(2)
主视图
左视图
俯视图
(3)
主视图
左视图
俯视图
(4)
主视图
左视图
俯视图
7. 一个几何体的三视图如图所示,画出该几何体.
2
2
2
2
左视图
俯视图
主视图
2
解:如图所示.
几何体、三视图和展开图之间的关系:
1.几何体的三视图和展开图是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性.
小结
小结
如何把组合体的三视图还原成几何体的实形:
1. 把每个视图分解为基本图形(三角形,圆等);
2. 结合对应部分的三视图想象对应的基本几何体;
3. 结合虚实线概括组合体.
第3章 投影与视图
3.3 三视图
第2课时 由三视图判断几何体
1.会从投影角度理解视图的概念.(重点)
2.会画简单几何体的三视图.(重难点)
3.能根据三视图想象简单几何体的形状.(重难点)
4.通过观察和动手实践,体会立体图形→三视图→立体图形的转换过程,培养空间观念.
学习目标
课时导入
问题1 如图所示的三视图表示什么立体图形?
从三个方向看立体图形,图形都是矩形,因此这个物体是长方体.
说一说
问题2 如图所示的三视图表示什么立体图形?
从正面,左面看立体图形,图形都是矩形,从上面看是圆形,因此这个物体是圆柱.
方法总结
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
根据图示三视图描述物体的形状?
分析:从主视图可知,物体的正面是矩形的样子,且中间有一条棱(实线)可见到;由俯视图可知,物体是矩形的样子,且中间有两条棱可见到;由左视图可知,物体的侧面是正六边形的样子.综合各视图可知,该物体是正六棱柱.
主视图
左视图
俯视图
例1
解:物体是正六棱柱,如图所示.
例2
解:这个零件由两部分构成:上面一个是圆柱、下面一个是长方体,圆柱立于长方体的中央.
如图是一个零件的三视图,试描述出这个零件的形状.
主视图
左视图
俯视图
随 堂 小 测
1.如图是某工件的三视图,其中圆的半径是 10 cm,等腰三角形的高是 30 cm,则此工件的体积是 ( )
A.1500π cm3 B.500π cm3
C.1000π cm3 D.2000π cm3
C
C
2.已知某物体的三视图如图所示,那么与它对应的物体是( )
3.一个立体图形的三视图如图所示,则这个立体图形是( )
D
4.一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,最少需用________个小正方体.
6
解:(1)此模型由两个长方体组成:上面是一个小长方体,下面是一个大长方体.
5.已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)模型的体积为10×6×5+3×1.5×2=309(m3),则该模型的质量为309×360=111 240(kg).
(2)制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少千克?
(3)模型的表面积为3×2×2+2×1.5×2+10×5×2+6×5×2+10×6×2=298(m2),
需要油漆298÷4=74.5(kg).
(3)如果要给这个模型刷油漆,每千克油漆可以刷4 m2,需要油漆多少千克?
6.请根据下面提供的三视图,画出几何图形.
(1)
主视图
左视图
俯视图
(2)
主视图
左视图
俯视图
(3)
主视图
左视图
俯视图
(4)
主视图
左视图
俯视图
7. 一个几何体的三视图如图所示,画出该几何体.
2
2
2
2
左视图
俯视图
主视图
2
解:如图所示.
几何体、三视图和展开图之间的关系:
1.几何体的三视图和展开图是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2.一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性.
小结
小结
如何把组合体的三视图还原成几何体的实形:
1. 把每个视图分解为基本图形(三角形,圆等);
2. 结合对应部分的三视图想象对应的基本几何体;
3. 结合虚实线概括组合体.
