4.2.1 概率的概念 课件 (共25张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 4.2.1 概率的概念 课件 (共25张PPT) 2023-2024学年数学湘教版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 582.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:30:52 | ||
图片预览







文档简介
(共25张PPT)
第4章 概率
4.2 概率及其计算
4.2.1 概率的概念
1.了解事件的概率,掌握求随机事件概率的方法.
2.会用列表法和树状图法分析简单随机事件所有等可能的结果,并求随机事件的概率.
学习目标
重点:概率的意义与计算.
难点:1.正确认识概率的意义;
2.用列表法和树状图法列举简单随机事件的所有等可能结果以及指定
事件的概率.
知识回顾
必然事件:在一定条件下必然发生的事件.
不可能事件:在一定条件下不可能发生的事件.
随机事件:在一定条件下可能发生也可能不发生的事件.
问题 回顾一下上节课学到的“必然事件”“不可能事 件”“随机事件”的定义.
课时导入
守株待兔
随机事件发生的可能性究竟有多大?能否用数值来刻画呢?
随机事件
我可没我朋友那么笨呢!撞到树上去让你吃掉,你好好等着吧,哈哈!
我们来看两个试验:
1.在一个箱子里放有 1 个白球和 1 个红球,它们除颜色外,大小、质地都相同.现从箱子中随机取出 1 个球,每个球被取到的可能性一样大吗?__________.
那么我们可以用哪个数来表示取到红球的可能性?________.
取到白球的可能性是多大呢?________.
一样大
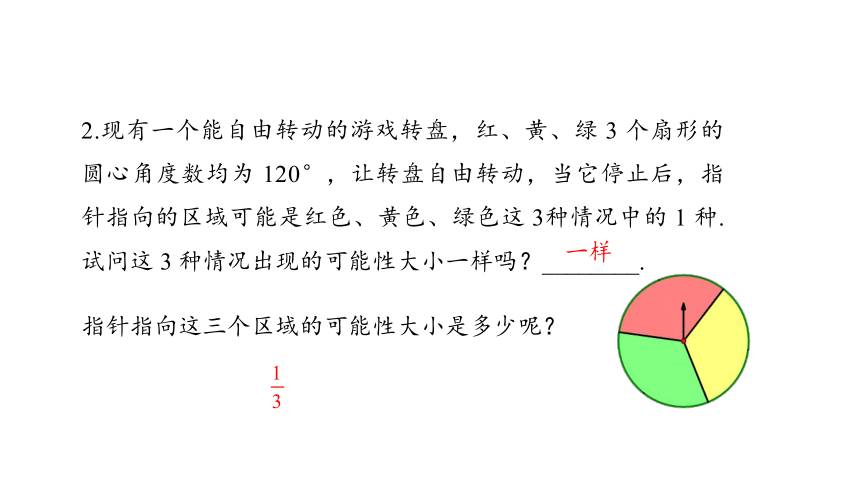
2.现有一个能自由转动的游戏转盘,红、黄、绿 3 个扇形的圆心角度数均为 120°,让转盘自由转动,当它停止后,指针指向的区域可能是红色、黄色、绿色这 3种情况中的 1 种.试问这 3 种情况出现的可能性大小一样吗?________.
一样
指针指向这三个区域的可能性大小是多少呢?
知识讲解
一般地,对于一个随机事件 A ,我们把刻画其发生可能性大小的数值,称为随机事件 A 发生的概率,记作 P(A).
例如,P(摸到红球) = .
动脑筋
把分别写有数字1,2,3,4,5,五张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取一个小纸团,试问:
(1) 取出的序号可能出现几种结果,每一个小纸团出现的可能性一样吗?
可能取出序号为 1,2,3,4,5中的任意一个小纸团;
每一个小纸团出现的可能性相同.
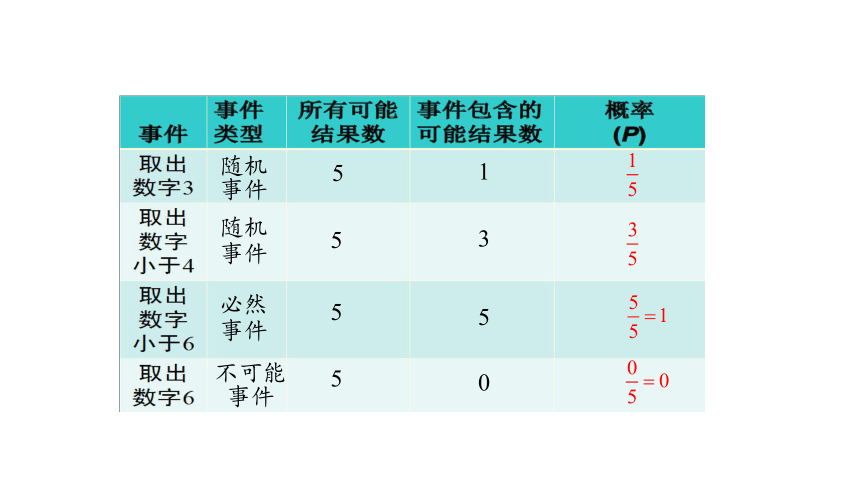
(2)下表中的事件分别是什么事件?它们的概率是多少?
5
5
5
5
1
3
5
0
随机事件
随机事件
必然事件
不可能事件
知识讲解
一般地,如果在一次试验中,有 n 种可能的结果,其中每一种结果发生的可能性相等,那么出现每一种结果的概率都是 .
如果事件 A 包括其中的 m 种可能的结果,那么事
件 A 发生的概率
事件 A 包含的可能结果数
一次试验所有可能出现的结果数
P(A) = + +…+
n
1
n
1
n
1
m个
=
n
m
∴
特别的
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
事件发生的概率越大,该事件就越有可能发生.
在上式中
例
假定按同一种方式掷两枚均匀硬币,如果第一枚出现正面(即正面朝上),第二枚出现反面,记为(正,反),如此类推.
(1) 写出掷两枚硬币的所有可能结果.
( 正,反 )
( 正,正 )
( 反,反 )
( 反,正 )
(3) 求事件A、B、C 的概率.
(2) 写出下列随机事件发生的所有可能结果.
A:“两枚都出现反面”
B:“一枚出现正面,一枚现反面”
C:“至少有一枚现反面”
(反,反)
(正,反)
(反,正)
(正,反)
(反,反)
(反,正)
随 堂 小 测
1. 从 1,2,3,4,5,6,7,8,9,10 这十个数中随机取出一个数,取出的数是 3 的倍数的概率是 ( )
A. B. C. D.
B
2. 小玲在一次班会中参与知识抢答活动,现有语文题 6 个,数学题 5 个,综合题 9 个,她从中随机抽取 1 个,抽中数学题的概率是 ( )
A. B. C. D.
C
3. 一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B.
C. D.
解析:观察这个图可知,阴影区域(3 块) 的面积占总面积(9 块)的 ,故其概率为 . 故选 A.
A
当某一事件 A 发生的可能性大小与相关图形的面积大小有关时,概率的计算方法是事件 A 所有可能结果所组成的图形的面积与所有可能结果组成的总图形面积之比,即 P(A)= .
概率的求法关键是要找准两点:
(1) 全部情况的总数;(2) 符合条件的情况数目.
二者的比值就是其发生的概率.
知识讲解
4. 袋子里有 1 个红球,3 个白球和 5 个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P ( 摸到红球 ) = ;
P ( 摸到白球 ) = ;
P ( 摸到黄球 ) = .
6. 有一对酷爱运动的年轻夫妇给他们 12 个月大的婴儿拼排 3 块分别写有“20”,“23”和“北京”的字块,如果婴儿能够排成“2023北京”或“北京2023”.则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是_____.
7.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .
解:∵红灯亮 30 秒,黄灯亮 3 秒,绿灯亮 42 秒,
∴P(红灯亮) = .
8. 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1) 点数大于6;
(2) 点数为奇数;
(3) 点数大于0.
解:(1) 此事件为不可能事件,P (点数大于6) = 0.
(2) 点数为奇数有 3 种可能,即点数为 1,3,5,因此 P (点数为奇数) = .
(3) 此事件为必然事件,因此 P (点数大于0) = 1.
9.有 10 张正面分别写有 1,2,…,10 的卡片,背面图案相同. 将卡片背面朝上充分混匀后,从中随机抽取 1 张卡片,得到一个数. 设 A 为“得到的数是 5 ”,B 为“得到的数是偶数”,C 为“得到的数能被 3 整除”,求事件 A,B,C 发生的概率.
解:试验共有 10 种可能结果,每个数被抽到的可能性相等,则 A 包含 1 种可能结果,B 包含 5 种可能结果,C 包含 3 种可能结果.
所以 P ( A ) = ,P ( B ) = ,P ( C ) = .
10.如图是计算机中“扫雷”游戏的画面.在一个有 9×9 的方格的正方形雷区中,随机埋藏着 10 颗地雷,每个方格内最多只能藏 1 颗地雷.
小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号 3 的方格相邻的方格记为 A 区域(画线部分),A 区域外的部分记为 B 区域.数字 3 表示在 A 区域有 3 颗地雷.下一步应该点击 A 区域还是 B 区域?
解:A 区域的方格总共有 8 个,标号 3 表示在这 8 个方格中有 3 个方格各藏有 1 颗地雷.因此,点击 A 区域的任一方格,遇到地雷的概率是 ;B 区域方格数为 9×9-9 = 72,其中有地雷的方格数为10-3 = 7.因此,点击 B 区域的任一方格,遇到地雷的概率是 ;
由于 即点击 A 区域遇到地雷的可能性大于点击 B 区域遇到地雷的可能性,因而第二步应该点击 B 区域.
小结
2. 必然事件 A ,则 P(A) = 1;不可能事件 B ,则 P(B) = 0;
随机事件 C ,则 0 < P(C) <1.
事件发生的概率越大,则该事件就越有可能发生.
1. 概率的定义及基本性质
如果在一次实验中,有 n 种可能的结果,并且他们发生的可能性都相等,事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0 ≤ m ≤ n,有 0 ≤ ≤ 1
第4章 概率
4.2 概率及其计算
4.2.1 概率的概念
1.了解事件的概率,掌握求随机事件概率的方法.
2.会用列表法和树状图法分析简单随机事件所有等可能的结果,并求随机事件的概率.
学习目标
重点:概率的意义与计算.
难点:1.正确认识概率的意义;
2.用列表法和树状图法列举简单随机事件的所有等可能结果以及指定
事件的概率.
知识回顾
必然事件:在一定条件下必然发生的事件.
不可能事件:在一定条件下不可能发生的事件.
随机事件:在一定条件下可能发生也可能不发生的事件.
问题 回顾一下上节课学到的“必然事件”“不可能事 件”“随机事件”的定义.
课时导入
守株待兔
随机事件发生的可能性究竟有多大?能否用数值来刻画呢?
随机事件
我可没我朋友那么笨呢!撞到树上去让你吃掉,你好好等着吧,哈哈!
我们来看两个试验:
1.在一个箱子里放有 1 个白球和 1 个红球,它们除颜色外,大小、质地都相同.现从箱子中随机取出 1 个球,每个球被取到的可能性一样大吗?__________.
那么我们可以用哪个数来表示取到红球的可能性?________.
取到白球的可能性是多大呢?________.
一样大
2.现有一个能自由转动的游戏转盘,红、黄、绿 3 个扇形的圆心角度数均为 120°,让转盘自由转动,当它停止后,指针指向的区域可能是红色、黄色、绿色这 3种情况中的 1 种.试问这 3 种情况出现的可能性大小一样吗?________.
一样
指针指向这三个区域的可能性大小是多少呢?
知识讲解
一般地,对于一个随机事件 A ,我们把刻画其发生可能性大小的数值,称为随机事件 A 发生的概率,记作 P(A).
例如,P(摸到红球) = .
动脑筋
把分别写有数字1,2,3,4,5,五张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取一个小纸团,试问:
(1) 取出的序号可能出现几种结果,每一个小纸团出现的可能性一样吗?
可能取出序号为 1,2,3,4,5中的任意一个小纸团;
每一个小纸团出现的可能性相同.
(2)下表中的事件分别是什么事件?它们的概率是多少?
5
5
5
5
1
3
5
0
随机事件
随机事件
必然事件
不可能事件
知识讲解
一般地,如果在一次试验中,有 n 种可能的结果,其中每一种结果发生的可能性相等,那么出现每一种结果的概率都是 .
如果事件 A 包括其中的 m 种可能的结果,那么事
件 A 发生的概率
事件 A 包含的可能结果数
一次试验所有可能出现的结果数
P(A) = + +…+
n
1
n
1
n
1
m个
=
n
m
∴
特别的
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
事件发生的概率越大,该事件就越有可能发生.
在上式中
例
假定按同一种方式掷两枚均匀硬币,如果第一枚出现正面(即正面朝上),第二枚出现反面,记为(正,反),如此类推.
(1) 写出掷两枚硬币的所有可能结果.
( 正,反 )
( 正,正 )
( 反,反 )
( 反,正 )
(3) 求事件A、B、C 的概率.
(2) 写出下列随机事件发生的所有可能结果.
A:“两枚都出现反面”
B:“一枚出现正面,一枚现反面”
C:“至少有一枚现反面”
(反,反)
(正,反)
(反,正)
(正,反)
(反,反)
(反,正)
随 堂 小 测
1. 从 1,2,3,4,5,6,7,8,9,10 这十个数中随机取出一个数,取出的数是 3 的倍数的概率是 ( )
A. B. C. D.
B
2. 小玲在一次班会中参与知识抢答活动,现有语文题 6 个,数学题 5 个,综合题 9 个,她从中随机抽取 1 个,抽中数学题的概率是 ( )
A. B. C. D.
C
3. 一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B.
C. D.
解析:观察这个图可知,阴影区域(3 块) 的面积占总面积(9 块)的 ,故其概率为 . 故选 A.
A
当某一事件 A 发生的可能性大小与相关图形的面积大小有关时,概率的计算方法是事件 A 所有可能结果所组成的图形的面积与所有可能结果组成的总图形面积之比,即 P(A)= .
概率的求法关键是要找准两点:
(1) 全部情况的总数;(2) 符合条件的情况数目.
二者的比值就是其发生的概率.
知识讲解
4. 袋子里有 1 个红球,3 个白球和 5 个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P ( 摸到红球 ) = ;
P ( 摸到白球 ) = ;
P ( 摸到黄球 ) = .
6. 有一对酷爱运动的年轻夫妇给他们 12 个月大的婴儿拼排 3 块分别写有“20”,“23”和“北京”的字块,如果婴儿能够排成“2023北京”或“北京2023”.则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是_____.
7.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .
解:∵红灯亮 30 秒,黄灯亮 3 秒,绿灯亮 42 秒,
∴P(红灯亮) = .
8. 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1) 点数大于6;
(2) 点数为奇数;
(3) 点数大于0.
解:(1) 此事件为不可能事件,P (点数大于6) = 0.
(2) 点数为奇数有 3 种可能,即点数为 1,3,5,因此 P (点数为奇数) = .
(3) 此事件为必然事件,因此 P (点数大于0) = 1.
9.有 10 张正面分别写有 1,2,…,10 的卡片,背面图案相同. 将卡片背面朝上充分混匀后,从中随机抽取 1 张卡片,得到一个数. 设 A 为“得到的数是 5 ”,B 为“得到的数是偶数”,C 为“得到的数能被 3 整除”,求事件 A,B,C 发生的概率.
解:试验共有 10 种可能结果,每个数被抽到的可能性相等,则 A 包含 1 种可能结果,B 包含 5 种可能结果,C 包含 3 种可能结果.
所以 P ( A ) = ,P ( B ) = ,P ( C ) = .
10.如图是计算机中“扫雷”游戏的画面.在一个有 9×9 的方格的正方形雷区中,随机埋藏着 10 颗地雷,每个方格内最多只能藏 1 颗地雷.
小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号 3 的方格相邻的方格记为 A 区域(画线部分),A 区域外的部分记为 B 区域.数字 3 表示在 A 区域有 3 颗地雷.下一步应该点击 A 区域还是 B 区域?
解:A 区域的方格总共有 8 个,标号 3 表示在这 8 个方格中有 3 个方格各藏有 1 颗地雷.因此,点击 A 区域的任一方格,遇到地雷的概率是 ;B 区域方格数为 9×9-9 = 72,其中有地雷的方格数为10-3 = 7.因此,点击 B 区域的任一方格,遇到地雷的概率是 ;
由于 即点击 A 区域遇到地雷的可能性大于点击 B 区域遇到地雷的可能性,因而第二步应该点击 B 区域.
小结
2. 必然事件 A ,则 P(A) = 1;不可能事件 B ,则 P(B) = 0;
随机事件 C ,则 0 < P(C) <1.
事件发生的概率越大,则该事件就越有可能发生.
1. 概率的定义及基本性质
如果在一次实验中,有 n 种可能的结果,并且他们发生的可能性都相等,事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0 ≤ m ≤ n,有 0 ≤ ≤ 1
