2.6 弧长与扇形面积 第1课时 弧长 课件(共22张PPT) 2023-2024学年数学湘教版九年级下册
文档属性
| 名称 | 2.6 弧长与扇形面积 第1课时 弧长 课件(共22张PPT) 2023-2024学年数学湘教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 11:41:58 | ||
图片预览







文档简介
(共22张PPT)
第2章 圆
第1课时 弧长
2.6 弧长与扇形面积
1.经历探索弧长、扇形面积公式的过程,进一步加深对圆的旋转对称性质的理解.(重难点)
2.会恰当运用公式计算弧长及扇形面积.
学习目标
课时导入
动脑筋
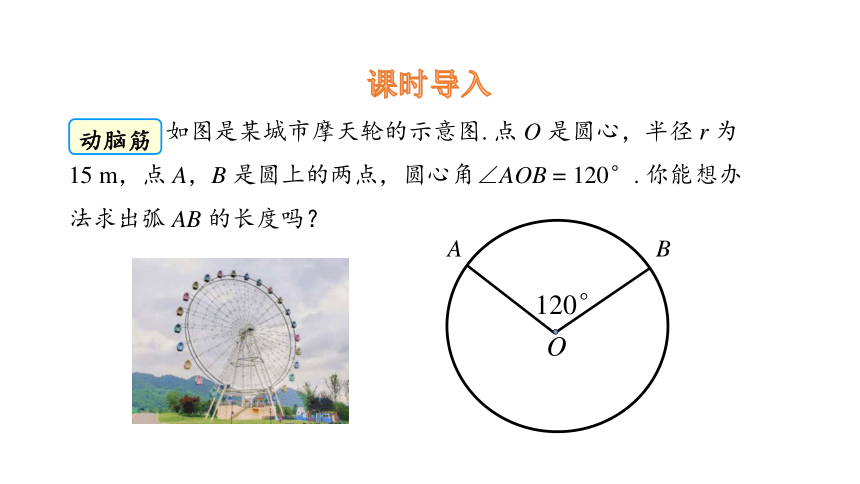
如图是某城市摩天轮的示意图. 点 O 是圆心,半径 r 为15 m,点 A,B 是圆上的两点,圆心角∠AOB = 120°. 你能想办法求出弧 AB 的长度吗?
120°
O
A
B
因为∠AOB = 120°,
所以弧 AB 的长是圆周长的 ,
因此弧 AB 的长为×2π×15 = 10π(m).
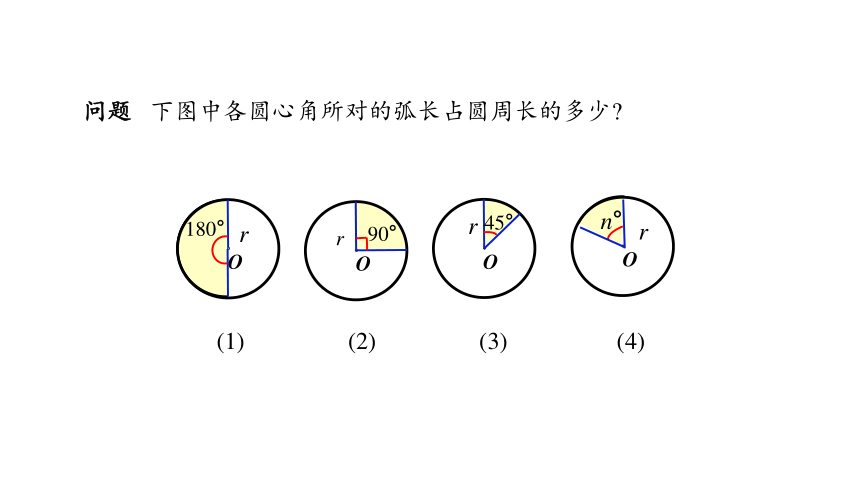
问题 下图中各圆心角所对的弧长占圆周长的多少
O
r
180°
O
r
90°
O
r
45°
O
r
n°
(1) (2) (3) (4)
(1) 圆心角是 180°,占整个周角的 ,因此它所对的弧长是圆周长的
(2) 圆心角是 90°,占整个周角的 ,因此它所对的弧长是圆周长的
(3) 圆心角是 45°,占整个周角的 ,因此它所对的弧长是圆周长的
(4) 圆心角是 n°,占整个周角的 ,因此它所对的弧长是圆周长的
________.
________.
________.
________.
知识讲解
(1)用弧长公式 进行计算时,要注意公式中 n
的意义.n 表示 1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
半径为 r 的圆中,n°的圆心角所对的弧长 l 为
在弧长公式中,R,n,l 三个量,可以做到知二求一:, .
扇形的周长公式:C扇形 = 2R .
例1
已知圆 O 的半径为 30 cm,求 40°的圆心角所对的弧长(精确到 0.1 cm).
解:
例2
解:由图可知,由于∠A'CB' = 60°,
则等边三角形木板绕点 C 按顺时针方向旋转了120°,即∠ACA' = 120°,这说明顶点 A 经过的路程长等于 的长.
∵等边三角形 ABC 的边长为 10 cm,
∴ 所在圆的半径为 10 cm,
∴
如图,一个边长为 10 cm 的等边三角形木板ABC在水平桌面上绕顶点 C 按顺时针方向旋转到△A'B'C的位置,求顶点 A 从开始到结束所经过的路程为多少.
A
B
A'
B'
C
答:顶点 A 从开始到结束时所经过的路程为
随 堂 小 测
1.圆心角为 120°,弧长为 12π 的扇形的半径为( )
A.6 B.9
C.18 D.36
C
2.一个扇形的弧长是 11π cm,半径是 18 cm,则此扇形的圆心角是( )
A.90° B.100°
C.110° D.120°
C
3. 钟表的轴心到分针针端的长为 5 cm,那么经过 40 分钟,分针针端转过的弧长是( )
A. B.
C. D.
B
4.如图,正方形 ABCD 内接于☉O,AB = 2,则 AB 的长是( )
A.π B. π
C.2π D. π
︵
A
5.如图,等边三角形 ABC 的三个顶点都在☉O 上,AD 是☉O
的直径.若 OA = 3,则劣弧 BD 的长是( )
A. B. π C. D. 2π
B
6.如图,实线部分是由两条等弧组成的游泳池,且这两条弧所在的圆的半径均为 15 m. 若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长是 m.
40π
解:如图,连接 O1O2,CO1,CO2,DO1,DO2.
∵O1O2 = CO1 = CO2 = 15 m,
∴ ∠CO1O2 = ∠CO2O1 = 60°,
同理,∠CO1D = ∠CO2D = 120°,
∴ 游泳池的周长为 2× = 2× = 40π (m).
7.如图,CD 为☉O 的弦,直径 AB 为 4,AB⊥CD 于 E,∠A = 30°,则弧 BC 的长为__________( 结果保留 π ).
8.如图,矩形ABCD中,AB=4,BC=3,边CD在直线 l 上,将矩形ABCD沿直线 l 作无滑动翻滚,当点A第一次翻滚到点A1的位置时,则点A经过的路线长为 .
解:点 A 的运动路径如图所示.
∵ 四边形 ABCD 是矩形,AB = 4,BC = 3,
∴ BC = AD = 3,∠ADC = 90°,对角线长为 5.
∵根据题意知,∠ADA′ = 90°,AD = A′D = BC = 3,
A
B
C
D
C′
B′
B′′
B′′
B1
C1
D1
A1
A′
……
6π
∴点 A 第一次翻滚到点 A′ 位置时,
则点 A 经过的路线长为 .
同理,点 A′ 翻滚到点 A″ 的位置时,
点 A 经过的路线长为 = 2π.
D1
A
B
C
D
C′
B′
B′′
B′′
B1
C1
A1
A′
点 A″ 翻滚到点 A1 的位置时,
点 A 经过的路线长为 .
∴当点 A 第一次翻滚到点 A1 的位置时,
点 A 经过的路线长为 +2π+ = 6π.
9.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度 l . (单位:mm,精确到 1 mm)
因此所要求的展直长度 l = 2×700+1570 ≈ 2 970 (mm) .
答:管道的展直长度约为 2970 mm.
700 mm
700 mm
R=900 mm
(
100°
A
C
B
D
O
解:由弧长公式,可得 的长
·
O
A
解:设半径 OA 绕轴心 O 逆时针方向旋转的度数为n°.
解得 n≈90°
因此,滑轮旋转的角度约为90°.
10.一滑轮起重机装置(如图),滑轮的半径 r = 10 cm,当重物上升15.7 cm 时,滑轮的一条半径 OA 绕轴心 O 逆时针方向旋转多少度(假设绳索与滑轮之间没有滑动,π取3.14)?
∴
小结
弧长
计算公式:
第2章 圆
第1课时 弧长
2.6 弧长与扇形面积
1.经历探索弧长、扇形面积公式的过程,进一步加深对圆的旋转对称性质的理解.(重难点)
2.会恰当运用公式计算弧长及扇形面积.
学习目标
课时导入
动脑筋
如图是某城市摩天轮的示意图. 点 O 是圆心,半径 r 为15 m,点 A,B 是圆上的两点,圆心角∠AOB = 120°. 你能想办法求出弧 AB 的长度吗?
120°
O
A
B
因为∠AOB = 120°,
所以弧 AB 的长是圆周长的 ,
因此弧 AB 的长为×2π×15 = 10π(m).
问题 下图中各圆心角所对的弧长占圆周长的多少
O
r
180°
O
r
90°
O
r
45°
O
r
n°
(1) (2) (3) (4)
(1) 圆心角是 180°,占整个周角的 ,因此它所对的弧长是圆周长的
(2) 圆心角是 90°,占整个周角的 ,因此它所对的弧长是圆周长的
(3) 圆心角是 45°,占整个周角的 ,因此它所对的弧长是圆周长的
(4) 圆心角是 n°,占整个周角的 ,因此它所对的弧长是圆周长的
________.
________.
________.
________.
知识讲解
(1)用弧长公式 进行计算时,要注意公式中 n
的意义.n 表示 1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
半径为 r 的圆中,n°的圆心角所对的弧长 l 为
在弧长公式中,R,n,l 三个量,可以做到知二求一:, .
扇形的周长公式:C扇形 = 2R .
例1
已知圆 O 的半径为 30 cm,求 40°的圆心角所对的弧长(精确到 0.1 cm).
解:
例2
解:由图可知,由于∠A'CB' = 60°,
则等边三角形木板绕点 C 按顺时针方向旋转了120°,即∠ACA' = 120°,这说明顶点 A 经过的路程长等于 的长.
∵等边三角形 ABC 的边长为 10 cm,
∴ 所在圆的半径为 10 cm,
∴
如图,一个边长为 10 cm 的等边三角形木板ABC在水平桌面上绕顶点 C 按顺时针方向旋转到△A'B'C的位置,求顶点 A 从开始到结束所经过的路程为多少.
A
B
A'
B'
C
答:顶点 A 从开始到结束时所经过的路程为
随 堂 小 测
1.圆心角为 120°,弧长为 12π 的扇形的半径为( )
A.6 B.9
C.18 D.36
C
2.一个扇形的弧长是 11π cm,半径是 18 cm,则此扇形的圆心角是( )
A.90° B.100°
C.110° D.120°
C
3. 钟表的轴心到分针针端的长为 5 cm,那么经过 40 分钟,分针针端转过的弧长是( )
A. B.
C. D.
B
4.如图,正方形 ABCD 内接于☉O,AB = 2,则 AB 的长是( )
A.π B. π
C.2π D. π
︵
A
5.如图,等边三角形 ABC 的三个顶点都在☉O 上,AD 是☉O
的直径.若 OA = 3,则劣弧 BD 的长是( )
A. B. π C. D. 2π
B
6.如图,实线部分是由两条等弧组成的游泳池,且这两条弧所在的圆的半径均为 15 m. 若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长是 m.
40π
解:如图,连接 O1O2,CO1,CO2,DO1,DO2.
∵O1O2 = CO1 = CO2 = 15 m,
∴ ∠CO1O2 = ∠CO2O1 = 60°,
同理,∠CO1D = ∠CO2D = 120°,
∴ 游泳池的周长为 2× = 2× = 40π (m).
7.如图,CD 为☉O 的弦,直径 AB 为 4,AB⊥CD 于 E,∠A = 30°,则弧 BC 的长为__________( 结果保留 π ).
8.如图,矩形ABCD中,AB=4,BC=3,边CD在直线 l 上,将矩形ABCD沿直线 l 作无滑动翻滚,当点A第一次翻滚到点A1的位置时,则点A经过的路线长为 .
解:点 A 的运动路径如图所示.
∵ 四边形 ABCD 是矩形,AB = 4,BC = 3,
∴ BC = AD = 3,∠ADC = 90°,对角线长为 5.
∵根据题意知,∠ADA′ = 90°,AD = A′D = BC = 3,
A
B
C
D
C′
B′
B′′
B′′
B1
C1
D1
A1
A′
……
6π
∴点 A 第一次翻滚到点 A′ 位置时,
则点 A 经过的路线长为 .
同理,点 A′ 翻滚到点 A″ 的位置时,
点 A 经过的路线长为 = 2π.
D1
A
B
C
D
C′
B′
B′′
B′′
B1
C1
A1
A′
点 A″ 翻滚到点 A1 的位置时,
点 A 经过的路线长为 .
∴当点 A 第一次翻滚到点 A1 的位置时,
点 A 经过的路线长为 +2π+ = 6π.
9.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度 l . (单位:mm,精确到 1 mm)
因此所要求的展直长度 l = 2×700+1570 ≈ 2 970 (mm) .
答:管道的展直长度约为 2970 mm.
700 mm
700 mm
R=900 mm
(
100°
A
C
B
D
O
解:由弧长公式,可得 的长
·
O
A
解:设半径 OA 绕轴心 O 逆时针方向旋转的度数为n°.
解得 n≈90°
因此,滑轮旋转的角度约为90°.
10.一滑轮起重机装置(如图),滑轮的半径 r = 10 cm,当重物上升15.7 cm 时,滑轮的一条半径 OA 绕轴心 O 逆时针方向旋转多少度(假设绳索与滑轮之间没有滑动,π取3.14)?
∴
小结
弧长
计算公式:
