2.2.1 第2课时 用配方法解二次项系数为1的一元二次方程 课件(共22张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 2.2.1 第2课时 用配方法解二次项系数为1的一元二次方程 课件(共22张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 813.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 23:46:42 | ||
图片预览








文档简介
(共22张PPT)
第2章 一元二次方程
2.2 一元二次方程的解法
2.2.1 配方法
第2课时 用配方法解二次项系数为1的一元二次方程
学习目标
1.理解配方法,知道用配方法解二次项系数为1的一元二次方程的基本步骤. (重点)
2.体会一元二次方程解法中的转化与降次思想.(难点)
复习引入
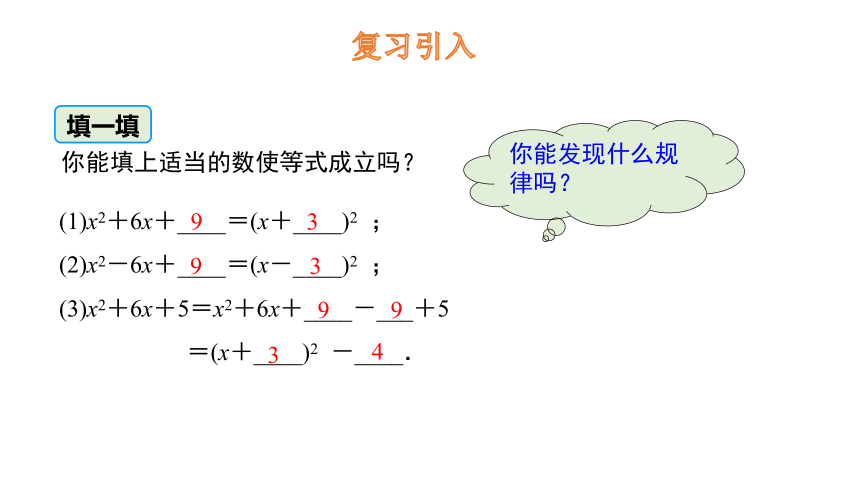
填一填
你能填上适当的数使等式成立吗?
(1)x2+6x+____=(x+____)2 ;
(2)x2-6x+____=(x-____)2 ;
(3)x2+6x+5=x2+6x+____-___+5
=(x+____)2 -____.
9
3
9
3
9
3
4
9
你能发现什么规律吗?
归纳总结
配方的方法:
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方.
即x2 + px + ( )2 = ( x + )2
知识讲解
知识点1 二次三项式的配方
例1: 填上适当的数或式,使下列各等式成立.
(1)x2 + 4x + = ( x + )2;
(2)x2 6x + = ( x )2;
(3)x2 + 8x + = ( x + )2;
x2 x + = ( x )2.
你发现了什么规律?
22
2
32
3
42
4
对于二次项系数为 1 的单字母二次三项式,将常数项配成一次项系数一半的平方时,可得完全平方公式.
在方程的左边加上一次项系数的一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里,这种做法叫配方.配方、整理后就可以直接根据平方根的意义来求解了.这种解一元二次方程的方法称为配方法.
配方法的定义
知识点2 用配方法解二次项系数为1的一元二次方程
探究交流
解方程:x2 + 4x - 12=0. (1)
问题1 方程 (1) 怎样变成 (x + n)2 = p 的形式呢?
解:
x2 + 4x - 12= 0
x2 + 4x = 12
移项
x2 + 4x + 4 = 12 + 4
两边都加上 4
二次项系数为 1 的完全平方式,常数项等于一次项系数一半的平方
问题2 为什么在方程 x2 + 4x = 12 的两边加上 4?加其他数行吗?
不行,只有在方程两边加上一次项系数一半的平方,方程左边才能变成完全平方式 x2 + 2mx + m2 的形式.
在方程两边都加上一次项系数一半的平方——注意是在二次项系数为 1 的前提下进行的.
一元二次方程配方的方法:
方法归纳
例2:用配方法解下列方程:
(1) x2 + 10x + 9 = 0;
解:
配方,得
x2 + 10x + 52-52 + 9 = 0,
因此 (x + 5)2 = 16,
由此得 x + 5 = 4 或 x + 5 = -4,
解得 x1 = -1,x2 = -9.
解:
配方,得 x2-12x + 62-62-13 = 0,
因此 (x-6)2 = 49,
由此得 x-6 = 7 或 x-6 = -7,
解得 x1 = 13,x2 = -1.
(2) x2 - 12x - 13 = 0.
用配方法解二次项系数为1的一元二次方程的步骤:
移项
配方
开方
求解
定解
把常数项移到方程的右边
方程两边都加上一次项系数一半的平方
方程两边开平方
解一元一次方程
写出原方程的解
方法归纳
变式:解方程 x2 + 8x -9 = 0 .
解:可以把常数项移到方程的右边,得x2 + 8x = 9,
两边都加 42 (一次项系数 8 的一半的平方),得x2 + 8x + 42 = 8 + 42 ,
即(x + 4)2 = 25.
两边开平方,得x + 4 = ,
即 x + 4 =5 或 x + 4 =-5 .
所以 x1 =1, x2 =-9 .
随 堂 小 测
1.将一元二次方程 x2 - 8x - 5 = 0化成 (x + a)2 = b 的形式,则 b 等于( )
A. -13 B. 13 C. -21 D. 21
D
2.已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( )
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
B
解:方程两边都除以3,得(x+1)2=,
开平方,得x+1=± ,即x+1=或x+1
∴x1=-,x2=-.
3.解下列方程
(1)3(x+1)2=;
解:开平方,得3x+2= ± 5,即 3x+2=5或3x+2=-5,
∴x1=1,x2=-.
(2)(3x+2)2=25;
解:
方程的两根为
4.解下列方程:
;
解:移项,得
x2-8x = -1.
配方,得
x2-8x + 42 = -1 + 42,
(x-4)2 = 15.
直接开平方得
即
5. 解方程: (x + 1 )(x - 1) + 2(x + 3) = 8.
解:方程化简,得 x2 + 2x + 5 = 8.
移项,得 x2 + 2x = 3,
配方,得x2 + 2x + 1 = 3 + 1,
即(x + 1)2 = 4.
开平方,得 x + 1 = ±2.
解得 x1 = 1, x2= -3.
6.如图,在Rt△ACB中,∠C=90°,AC=8m,CB=6m,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动,它们的速度都是1m/s,问几秒后△PCQ的面积Rt△ACB面积的一半?
解:设x秒后△PCQ的面积为Rt△ACB面积的一半.
所以2秒后△PCQ的面积为Rt△ACB面积的一半.
A
C
B
P
Q
整理,得x2-14x+24=0,
即(x-7)2=25,解得x1=12,x2=2,
x1=12,x2=2都是原方程的根,但x1=12不合题意,舍去.
小结
用配方法解
一元二次方程
基本思路
将方程转化为(x + m)2 = n (n≥0)的形
式,再用直接开平方法,直接求根
配方法解一元二次方程的步骤
1.移项
3.直接开平方求解
2.配方
第2章 一元二次方程
2.2 一元二次方程的解法
2.2.1 配方法
第2课时 用配方法解二次项系数为1的一元二次方程
学习目标
1.理解配方法,知道用配方法解二次项系数为1的一元二次方程的基本步骤. (重点)
2.体会一元二次方程解法中的转化与降次思想.(难点)
复习引入
填一填
你能填上适当的数使等式成立吗?
(1)x2+6x+____=(x+____)2 ;
(2)x2-6x+____=(x-____)2 ;
(3)x2+6x+5=x2+6x+____-___+5
=(x+____)2 -____.
9
3
9
3
9
3
4
9
你能发现什么规律吗?
归纳总结
配方的方法:
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方.
即x2 + px + ( )2 = ( x + )2
知识讲解
知识点1 二次三项式的配方
例1: 填上适当的数或式,使下列各等式成立.
(1)x2 + 4x + = ( x + )2;
(2)x2 6x + = ( x )2;
(3)x2 + 8x + = ( x + )2;
x2 x + = ( x )2.
你发现了什么规律?
22
2
32
3
42
4
对于二次项系数为 1 的单字母二次三项式,将常数项配成一次项系数一半的平方时,可得完全平方公式.
在方程的左边加上一次项系数的一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里,这种做法叫配方.配方、整理后就可以直接根据平方根的意义来求解了.这种解一元二次方程的方法称为配方法.
配方法的定义
知识点2 用配方法解二次项系数为1的一元二次方程
探究交流
解方程:x2 + 4x - 12=0. (1)
问题1 方程 (1) 怎样变成 (x + n)2 = p 的形式呢?
解:
x2 + 4x - 12= 0
x2 + 4x = 12
移项
x2 + 4x + 4 = 12 + 4
两边都加上 4
二次项系数为 1 的完全平方式,常数项等于一次项系数一半的平方
问题2 为什么在方程 x2 + 4x = 12 的两边加上 4?加其他数行吗?
不行,只有在方程两边加上一次项系数一半的平方,方程左边才能变成完全平方式 x2 + 2mx + m2 的形式.
在方程两边都加上一次项系数一半的平方——注意是在二次项系数为 1 的前提下进行的.
一元二次方程配方的方法:
方法归纳
例2:用配方法解下列方程:
(1) x2 + 10x + 9 = 0;
解:
配方,得
x2 + 10x + 52-52 + 9 = 0,
因此 (x + 5)2 = 16,
由此得 x + 5 = 4 或 x + 5 = -4,
解得 x1 = -1,x2 = -9.
解:
配方,得 x2-12x + 62-62-13 = 0,
因此 (x-6)2 = 49,
由此得 x-6 = 7 或 x-6 = -7,
解得 x1 = 13,x2 = -1.
(2) x2 - 12x - 13 = 0.
用配方法解二次项系数为1的一元二次方程的步骤:
移项
配方
开方
求解
定解
把常数项移到方程的右边
方程两边都加上一次项系数一半的平方
方程两边开平方
解一元一次方程
写出原方程的解
方法归纳
变式:解方程 x2 + 8x -9 = 0 .
解:可以把常数项移到方程的右边,得x2 + 8x = 9,
两边都加 42 (一次项系数 8 的一半的平方),得x2 + 8x + 42 = 8 + 42 ,
即(x + 4)2 = 25.
两边开平方,得x + 4 = ,
即 x + 4 =5 或 x + 4 =-5 .
所以 x1 =1, x2 =-9 .
随 堂 小 测
1.将一元二次方程 x2 - 8x - 5 = 0化成 (x + a)2 = b 的形式,则 b 等于( )
A. -13 B. 13 C. -21 D. 21
D
2.已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( )
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
B
解:方程两边都除以3,得(x+1)2=,
开平方,得x+1=± ,即x+1=或x+1
∴x1=-,x2=-.
3.解下列方程
(1)3(x+1)2=;
解:开平方,得3x+2= ± 5,即 3x+2=5或3x+2=-5,
∴x1=1,x2=-.
(2)(3x+2)2=25;
解:
方程的两根为
4.解下列方程:
;
解:移项,得
x2-8x = -1.
配方,得
x2-8x + 42 = -1 + 42,
(x-4)2 = 15.
直接开平方得
即
5. 解方程: (x + 1 )(x - 1) + 2(x + 3) = 8.
解:方程化简,得 x2 + 2x + 5 = 8.
移项,得 x2 + 2x = 3,
配方,得x2 + 2x + 1 = 3 + 1,
即(x + 1)2 = 4.
开平方,得 x + 1 = ±2.
解得 x1 = 1, x2= -3.
6.如图,在Rt△ACB中,∠C=90°,AC=8m,CB=6m,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动,它们的速度都是1m/s,问几秒后△PCQ的面积Rt△ACB面积的一半?
解:设x秒后△PCQ的面积为Rt△ACB面积的一半.
所以2秒后△PCQ的面积为Rt△ACB面积的一半.
A
C
B
P
Q
整理,得x2-14x+24=0,
即(x-7)2=25,解得x1=12,x2=2,
x1=12,x2=2都是原方程的根,但x1=12不合题意,舍去.
小结
用配方法解
一元二次方程
基本思路
将方程转化为(x + m)2 = n (n≥0)的形
式,再用直接开平方法,直接求根
配方法解一元二次方程的步骤
1.移项
3.直接开平方求解
2.配方
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
