3.1.2 成比例线段 课件(共20张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.1.2 成比例线段 课件(共20张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第3章 图形的相似
3.1 比例线段
3.1.2 成比例线段
学习目标
1.了解线段的比和成比例线段的概念,通过实例了解“黄金分割”.
2.通过计算,判定四条线段是否成比例.
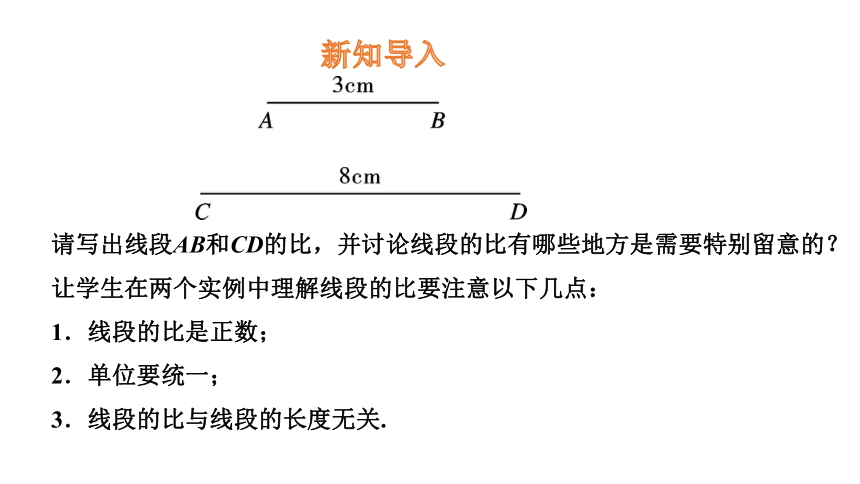
新知导入
请写出线段AB和CD的比,并讨论线段的比有哪些地方是需要特别留意的?
让学生在两个实例中理解线段的比要注意以下几点:
1.线段的比是正数;
2.单位要统一;
3.线段的比与线段的长度无关.
知识讲解
知识点1 线段的比和成比例线段
如果选用同一长度单位量得两条线段 AB,CD 的长度分别是 m, n,那么它们长度的比就是这两条线段的比,即
A
B
C
D
m
n
如果 的比值为 k,那么 = k,或 AB = k · CD,两条线段的比实际上就是两个数的比.
AB∶CD = m∶n 或
思考:两条线段长度的比与所采用的长度单位是否有关?
有关
无关
求两条线段的比时,所使用的长度单位应该统一.
在对长度单位进行统一时,无论采用哪一种单位,比值都相同.
注意:虽然两条线段的比要在单位统一的前提下进行,但比值却是一个不带单位的正数.
练一练
1.若线段 AB=6 cm,CD=4 cm,则
.
.
2.若线段 AB=8 cm,CD=2 dm,则
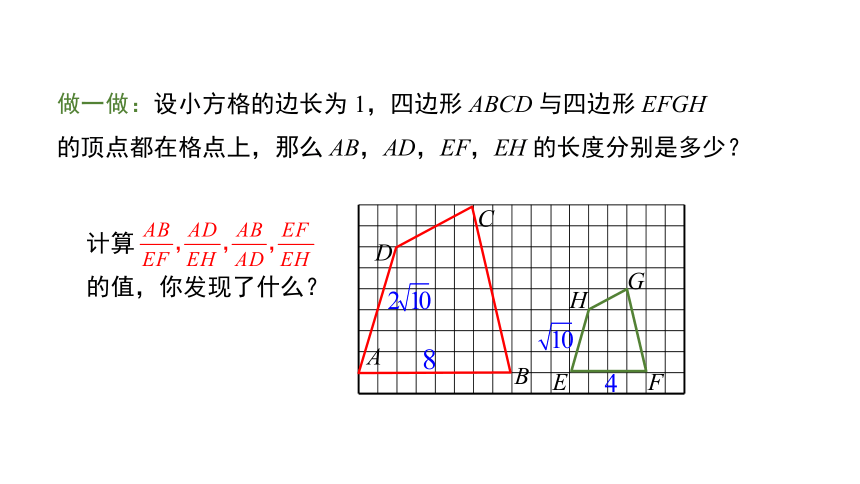
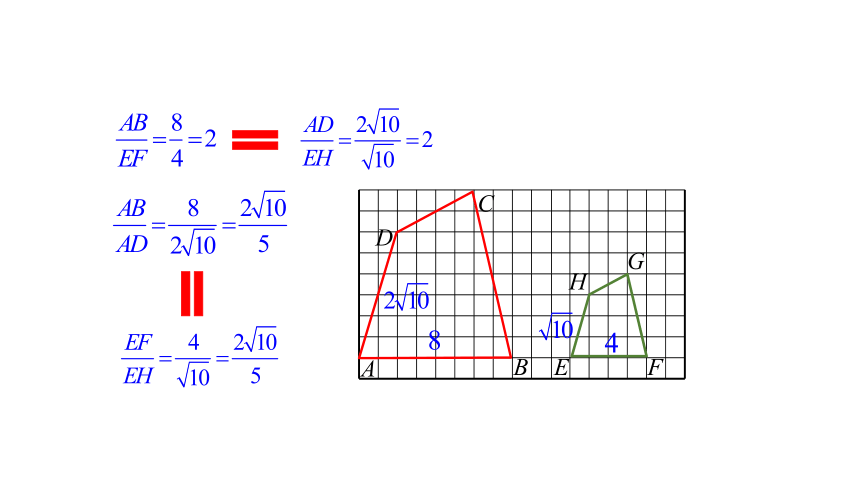
做一做:设小方格的边长为 1,四边形 ABCD 与四边形 EFGH 的顶点都在格点上,那么 AB,AD,EF,EH 的长度分别是多少?
A
B
C
D
G
H
E
F
计算
的值,你发现了什么?
A
B
C
D
G
H
E
F
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称为比例线段.
归纳总结
例如已知四条线段 a, b, c, d ,若 , 则 a, b, c, d 是比例线段.
类似地,如果 ,那么称线段 AB,BC,AC与线段 A′B′,B′C′,A′C′对应成比例.
例1 判断下列线段 a,b,c,d 是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解:(1)∵
∴ 线段 a,b,c,d 不是成比例线段.
, ,
∴
.
(2)a=2,b=
,c=
,d=
.
(2)∵
∴
∴ 线段 a,b,c,d 是成比例线段.
注意:
1.若 a∶b = k,说明 a 是 b 的 k 倍;
2.两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
3.两条线段的比值是一个没有单位的正数;
4.除了a = b 外,a∶b ≠ b∶a,与互为倒数.
解:根据题意可知,AB = a m,AE =a m,AD = 1 m .
例2 一块矩形绸布的长 AB = a m,宽 AD = 1 m,按照图中所示方式将它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么 a 的值应当是多少?
D
A
F
E
C
B
即 ,开平方,得a=.
由 ,得 = .
答:a 的值应当是m.
建筑中的神秘数字
古希腊的巴台农神殿,塔高与工作厅高之比为340∶553≈0.615.
绘画艺术中的黄金分割
黄金矩形的“迷人面容”
----蒙娜丽莎的微笑.
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇.意大利画家达芬奇在创作中大量运用了黄金矩形来构图.整个画面使人觉得和谐自然,优雅安宁.
例3 在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618越给人以美感.张女士的身高为1.68米,身体躯干(脚底到肚脐的高度)为1.02米,那么她应选择约多高的高跟鞋看起来更美.(精确到十分位)
解得x≈4.8cm.
故答案为4.8厘米.
随 堂 小 测
1.教室黑板长450cm,宽15dm,则长与宽的比为( )
A.30∶1 B.1∶3 C.3∶1 D.1∶30
2.在比例尺为1∶100000的地图上,量得A,B两地的距离是25cm,则A,B两地之间的实际距离为 .
25km
3.节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.若舞台AB长为20m,则主持人站在离A点多远处最自然得体?(结果精确到0.1m)
12.4 m或7.6 m
4.点 C 是线段 AB 的黄金分割点,如果 AB = 4,求线段 AC 的长度.
AC = 4×0.618 = 2.472 或者 AC = 4×(1 - 0.618) = 1.518.
注意:一定要分类讨论.此题容易漏解.
小结
两条线段的比
比例线段
比例线段
①求两条线段的比时,所使用的长度单位应该统一
②与单位无关,本身没有单位
③两条线段有顺序要求
①概念:项、比例内项、比例外项
②四条线段有顺序要求
③特别地:比例中项
第3章 图形的相似
3.1 比例线段
3.1.2 成比例线段
学习目标
1.了解线段的比和成比例线段的概念,通过实例了解“黄金分割”.
2.通过计算,判定四条线段是否成比例.
新知导入
请写出线段AB和CD的比,并讨论线段的比有哪些地方是需要特别留意的?
让学生在两个实例中理解线段的比要注意以下几点:
1.线段的比是正数;
2.单位要统一;
3.线段的比与线段的长度无关.
知识讲解
知识点1 线段的比和成比例线段
如果选用同一长度单位量得两条线段 AB,CD 的长度分别是 m, n,那么它们长度的比就是这两条线段的比,即
A
B
C
D
m
n
如果 的比值为 k,那么 = k,或 AB = k · CD,两条线段的比实际上就是两个数的比.
AB∶CD = m∶n 或
思考:两条线段长度的比与所采用的长度单位是否有关?
有关
无关
求两条线段的比时,所使用的长度单位应该统一.
在对长度单位进行统一时,无论采用哪一种单位,比值都相同.
注意:虽然两条线段的比要在单位统一的前提下进行,但比值却是一个不带单位的正数.
练一练
1.若线段 AB=6 cm,CD=4 cm,则
.
.
2.若线段 AB=8 cm,CD=2 dm,则
做一做:设小方格的边长为 1,四边形 ABCD 与四边形 EFGH 的顶点都在格点上,那么 AB,AD,EF,EH 的长度分别是多少?
A
B
C
D
G
H
E
F
计算
的值,你发现了什么?
A
B
C
D
G
H
E
F
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称为比例线段.
归纳总结
例如已知四条线段 a, b, c, d ,若 , 则 a, b, c, d 是比例线段.
类似地,如果 ,那么称线段 AB,BC,AC与线段 A′B′,B′C′,A′C′对应成比例.
例1 判断下列线段 a,b,c,d 是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解:(1)∵
∴ 线段 a,b,c,d 不是成比例线段.
, ,
∴
.
(2)a=2,b=
,c=
,d=
.
(2)∵
∴
∴ 线段 a,b,c,d 是成比例线段.
注意:
1.若 a∶b = k,说明 a 是 b 的 k 倍;
2.两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
3.两条线段的比值是一个没有单位的正数;
4.除了a = b 外,a∶b ≠ b∶a,与互为倒数.
解:根据题意可知,AB = a m,AE =a m,AD = 1 m .
例2 一块矩形绸布的长 AB = a m,宽 AD = 1 m,按照图中所示方式将它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么 a 的值应当是多少?
D
A
F
E
C
B
即 ,开平方,得a=.
由 ,得 = .
答:a 的值应当是m.
建筑中的神秘数字
古希腊的巴台农神殿,塔高与工作厅高之比为340∶553≈0.615.
绘画艺术中的黄金分割
黄金矩形的“迷人面容”
----蒙娜丽莎的微笑.
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇.意大利画家达芬奇在创作中大量运用了黄金矩形来构图.整个画面使人觉得和谐自然,优雅安宁.
例3 在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618越给人以美感.张女士的身高为1.68米,身体躯干(脚底到肚脐的高度)为1.02米,那么她应选择约多高的高跟鞋看起来更美.(精确到十分位)
解得x≈4.8cm.
故答案为4.8厘米.
随 堂 小 测
1.教室黑板长450cm,宽15dm,则长与宽的比为( )
A.30∶1 B.1∶3 C.3∶1 D.1∶30
2.在比例尺为1∶100000的地图上,量得A,B两地的距离是25cm,则A,B两地之间的实际距离为 .
25km
3.节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.若舞台AB长为20m,则主持人站在离A点多远处最自然得体?(结果精确到0.1m)
12.4 m或7.6 m
4.点 C 是线段 AB 的黄金分割点,如果 AB = 4,求线段 AC 的长度.
AC = 4×0.618 = 2.472 或者 AC = 4×(1 - 0.618) = 1.518.
注意:一定要分类讨论.此题容易漏解.
小结
两条线段的比
比例线段
比例线段
①求两条线段的比时,所使用的长度单位应该统一
②与单位无关,本身没有单位
③两条线段有顺序要求
①概念:项、比例内项、比例外项
②四条线段有顺序要求
③特别地:比例中项
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
