3.3 相似图形 课件(共20张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.3 相似图形 课件(共20张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1005.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第3章 图形的相似
3.3 相似图形
学习目标
1.通过具体实例认识图形的相似.
2.了解相似多边形、相似三角形和相似比.
3.知道相似三角形和相似多边形的定义.
课时导入
观察
下面两组图中,分别是由其中的一幅图放大或缩小得到的.把一个
图形放大(或缩小)得到的图形与原图形之间有什么关系呐?
知识讲解
知识点1 相似图形
直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的.
因此,上面两组图形分别是相似的.
在两个大小相等的相似图形中,我们可以认为大的图形是由小的图形放大而成,
或小的图形是由大的图形缩小而成.
日常生活中,常常需要将一个图形按一定的比例放大或者缩小,但不能改变其形状,
如制作不同尺寸的国际海事信号旗时,旗的形状是相同的,但大小不一样.
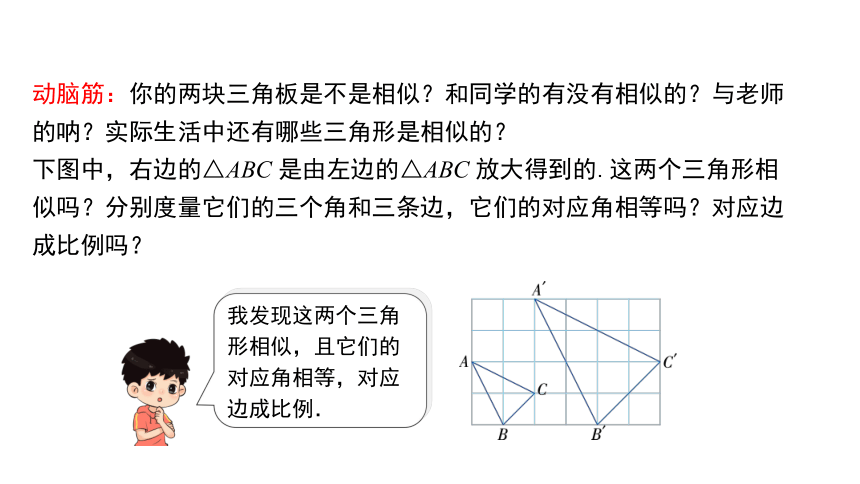
动脑筋:你的两块三角板是不是相似?和同学的有没有相似的?与老师的呐?实际生活中还有哪些三角形是相似的?
下图中,右边的△ABC 是由左边的△ABC 放大得到的.这两个三角形相似吗?分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例吗?
我发现这两个三角形相似,且它们的对应角相等,对应边成比例.
反过来,我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
由此得到相似三角形的性质:相似三角形的对应角相等,对应边成比例.
A
B
C
C'
B'
A'
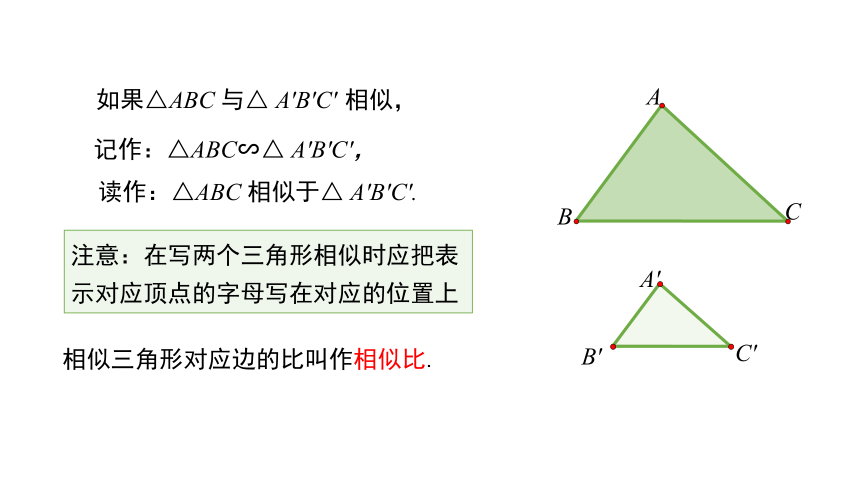
如果△ABC 与△ A'B'C' 相似,
记作:△ABC∽△ A'B'C',
读作:△ABC 相似于△ A'B'C'.
注意:在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上
相似三角形对应边的比叫作相似比.
注意:三角形的前后次序不同,所得相似比不同.
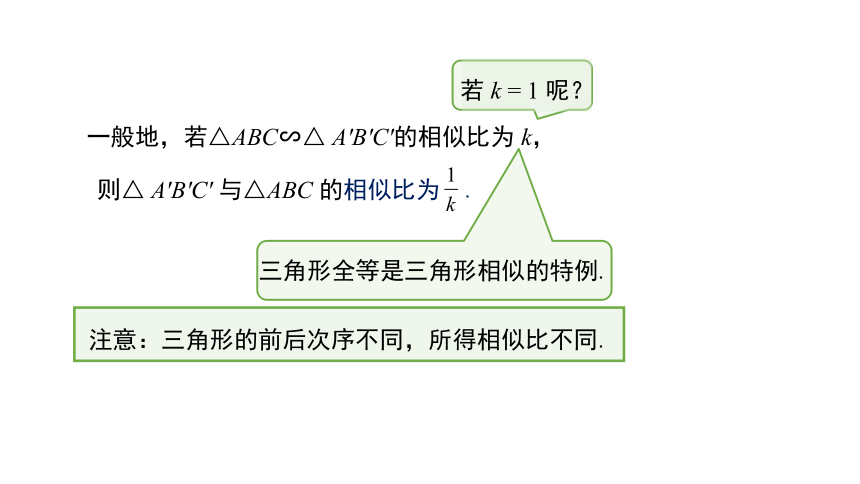
一般地,若△ABC∽△ A'B'C'的相似比为 k,
则△ A'B'C' 与△ABC 的相似比为 .
若 k = 1 呢?
三角形全等是三角形相似的特例.
例1:已知△ABC∽△ A'B'C',且∠A = 48°,AB = 8,A'B' = 4,AC = 6. 求∠A' 的大小和 A'C' 的长.
A
B
C
A'
B'
C'
解: 因为 △ABC∽△A'B'C' ,
又∠A = 48°,AB = 8,
A'B' = 4,AC = 6,
∴ ∠A' = 48°.
∴ A'C' = 3.
典例精析
知识点2 相似多边形和相似比
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
下面给出了两个多边形,多边形 ABCDEF 表示显示在电脑屏幕上的图形,而多边形A1B1C1D1E1F1 是多边形ABCDEF投射到银幕上的图形.
观察与思考
问题1 在这两个多边形中,是否有对应相等的内角?
问题2 在这两个多边形中,夹相等内角的两边是否对应成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
对应角相等、对应边成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
总结归纳
注:相似多边形用符号“∽”表示,读作“相似于”.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为 60°,三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
议一议
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
思考:
任意的两个菱形(或矩形)是否相似?为什么?
例2:如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的比相等,由此可得,
解得 a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为 3,4.5,4,6.
, , , ,
随 堂 小 测
1.观察下列的四组图形,不是相似图形的是( )
A
B
C
D
C
2.若一张地图的比例尺是 1:150000,在地图上量得甲、乙两地的距离是 5 cm,则甲、乙两地的实际距离是( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
3. 如图所示的两个四边形是否相似?
答案:不相似.
小结
相似三角形
相似图形
相似比:相似图形对应边的比叫做相似比
相似多边形
概念
性质:相似三角形的对应角相等,对应边成比例
概念
性质:相似多边形的对应角相等,对应边成比例
第3章 图形的相似
3.3 相似图形
学习目标
1.通过具体实例认识图形的相似.
2.了解相似多边形、相似三角形和相似比.
3.知道相似三角形和相似多边形的定义.
课时导入
观察
下面两组图中,分别是由其中的一幅图放大或缩小得到的.把一个
图形放大(或缩小)得到的图形与原图形之间有什么关系呐?
知识讲解
知识点1 相似图形
直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的.
因此,上面两组图形分别是相似的.
在两个大小相等的相似图形中,我们可以认为大的图形是由小的图形放大而成,
或小的图形是由大的图形缩小而成.
日常生活中,常常需要将一个图形按一定的比例放大或者缩小,但不能改变其形状,
如制作不同尺寸的国际海事信号旗时,旗的形状是相同的,但大小不一样.
动脑筋:你的两块三角板是不是相似?和同学的有没有相似的?与老师的呐?实际生活中还有哪些三角形是相似的?
下图中,右边的△ABC 是由左边的△ABC 放大得到的.这两个三角形相似吗?分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例吗?
我发现这两个三角形相似,且它们的对应角相等,对应边成比例.
反过来,我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
由此得到相似三角形的性质:相似三角形的对应角相等,对应边成比例.
A
B
C
C'
B'
A'
如果△ABC 与△ A'B'C' 相似,
记作:△ABC∽△ A'B'C',
读作:△ABC 相似于△ A'B'C'.
注意:在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上
相似三角形对应边的比叫作相似比.
注意:三角形的前后次序不同,所得相似比不同.
一般地,若△ABC∽△ A'B'C'的相似比为 k,
则△ A'B'C' 与△ABC 的相似比为 .
若 k = 1 呢?
三角形全等是三角形相似的特例.
例1:已知△ABC∽△ A'B'C',且∠A = 48°,AB = 8,A'B' = 4,AC = 6. 求∠A' 的大小和 A'C' 的长.
A
B
C
A'
B'
C'
解: 因为 △ABC∽△A'B'C' ,
又∠A = 48°,AB = 8,
A'B' = 4,AC = 6,
∴ ∠A' = 48°.
∴ A'C' = 3.
典例精析
知识点2 相似多边形和相似比
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
下面给出了两个多边形,多边形 ABCDEF 表示显示在电脑屏幕上的图形,而多边形A1B1C1D1E1F1 是多边形ABCDEF投射到银幕上的图形.
观察与思考
问题1 在这两个多边形中,是否有对应相等的内角?
问题2 在这两个多边形中,夹相等内角的两边是否对应成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
对应角相等、对应边成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
总结归纳
注:相似多边形用符号“∽”表示,读作“相似于”.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为 60°,三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
议一议
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
思考:
任意的两个菱形(或矩形)是否相似?为什么?
例2:如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的比相等,由此可得,
解得 a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为 3,4.5,4,6.
, , , ,
随 堂 小 测
1.观察下列的四组图形,不是相似图形的是( )
A
B
C
D
C
2.若一张地图的比例尺是 1:150000,在地图上量得甲、乙两地的距离是 5 cm,则甲、乙两地的实际距离是( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
3. 如图所示的两个四边形是否相似?
答案:不相似.
小结
相似三角形
相似图形
相似比:相似图形对应边的比叫做相似比
相似多边形
概念
性质:相似三角形的对应角相等,对应边成比例
概念
性质:相似多边形的对应角相等,对应边成比例
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
