3.4.1 第1课时 利用平行判定三角形相似 课件(共27张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.4.1 第1课时 利用平行判定三角形相似 课件(共27张PPT) 2023-2024学年数学湘教版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 14:54:32 | ||
图片预览








文档简介
(共27张PPT)
第3章 图形的相似
3.4 相似三角形的判定
3.4.1 相似三角形的判定
第1课时 利用平行判定三角形相似
学习目标
1.了解相似三角形的判定方法,即平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
2.会用平行判定三角形相似.
复习导入
在八年级上册,我们已经探讨了两个三角形全等的条件,下面我们来
探讨两个三角形相似的条件.
为了研究满足什么条件的两个三角形相似,我们先来研究下述问题.
知识讲解
知识点1 相似三角形的性质及有关概念
我们就说 △ABC 与 △A′B′C′______,记作__________________,△ABC 与 △A′B′C′ 相似比是 k,则 △A′B′C′ 与 △ABC 的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在 △ABC 与 △A′B′C′ 中,如果∠A = ∠A′, ∠B = ∠B′,∠C = ∠C′,且===k,
△ABC∽△A′B′C′
相似
反之如果 △ABC∽△A′B′C′,则有∠A =_____,∠B =_____,∠C =____,且
∠A′
∠B′
∠C′
相似比为 1 时,相似的
两个图形有什么关系?
当相似比等于 1 时,相似图形是全等图形,全等是一种特殊的相似.
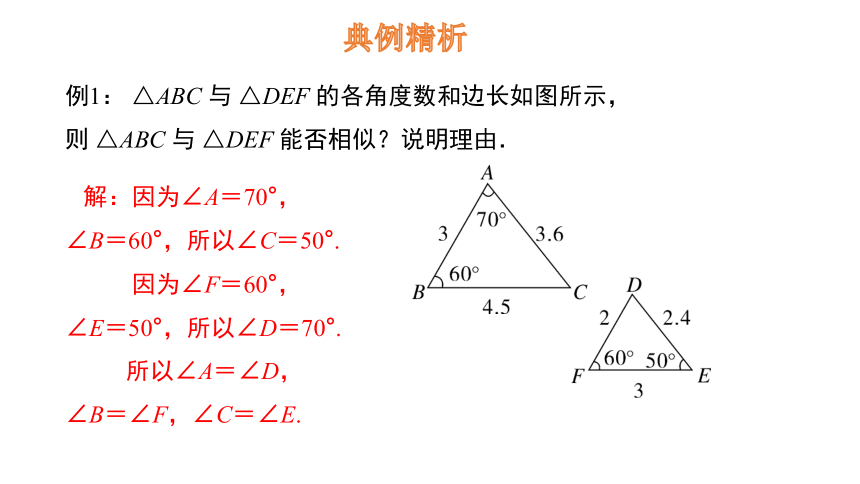
例1: △ABC 与 △DEF 的各角度数和边长如图所示,则 △ABC 与 △DEF 能否相似?说明理由.
解:因为∠A=70°,∠B=60°,所以∠C=50°.
因为∠F=60°,∠E=50°,所以∠D=70°.
所以∠A=∠D,∠B=∠F,∠C=∠E.
典例精析
∴ △ABC∽△DFE.
判断两个三角形相似,一定要具备两个条件:一是对应角相等,二是对应边成比例.另外在书写两个三角形相似时,一定要将对应的顶点写在对应的位置上.
方法总结
例2 :如图,已知 △ABC∽△ADE,AE=50 cm,EC=30 cm,BC=58 cm,∠BAC=45°,∠ACB=40°,求:
(1) ∠AED 和 ∠ADE 的度数;(2) DE 的长.
解:(1)∵△ABC∽△ADE,∴∠AED=∠ACB=40°.
在 △ADE 中,∠ADE=180°-40°-45°=95°.
(2) ∵△ABC∽△ADE.
∴ DE=36.25 cm.
当题目中有相似三角形(或能证明出相似三角形)时,首先考虑用相似三角形的性质,由性质既能得到相等的角,又能得到成比例的线段.
方法总结
知识点2 利用平行判定相似三角形
在△ABC 中,D为AB上任意一点,过点D作BC 的平行线DE,交AC于点E.
(1)△ADE 与△ABC 的三个角分别相等吗?
(2)分别度量△ADE与△ABC 的边长,它们的边长是否对应成比例?
(3)△ADE与△ABC之间有什么关系?平行移动DE 的位置,你的结论还成立吗?
我发现只要DE平行BC,那么三角形ADE与
三角形ABC是相似的.
A
B
C
D
下面我们来证明. 在 △ADE 与 △ABC 中,∠A = ∠A.
∵ DE∥BC,
∴∠ADE = ∠B, ∠AED = ∠C,
过 E 作 EF∥AB 交 BC 于 F,
F
E
∵四边形 DBFE 是平行四边形,
∴DE = BF.
∴△ADE∽△ABC.
A
B
C
D
F
E
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
归纳
例3: 如图,在△ABC 中,已知点 D,E 分别是 AB,AC边的中点. 求证:△ADE∽△ABC.
证明:∵点 D,E 分别是 AB,AC 边的中点,
∴ DE∥BC,
∴△ADE∽△ABC.
A
E
C
B
D
例4 :如图,点 D 作为△ABC 的边 AB 的中点,过点 D 作DE∥BC,交边 AC 于点 E.延长 DE 至点 F,使DE = EF.求证:△CFE∽△ABC.
解:∵DE∥BC,点 D 为△ABC 的边 AB 的中点,∴AE = CE.
又 DE = EF,∠AED = ∠CEF,
∴△ADE≌△CFE(SAS).
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
A
E
D
B
C
F
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
M
N
如果再作 MN∥DE ,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形
已知 DE∥BC,
交流讨论
如图,在 △ABC 中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果 AD = 1,DB = 3,那么 DG∶BC =_____.
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1∶4
练一练
随 堂 小 测
C
1.如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E.
若线段DE=5,则线段BC的长为( )
A.7.5 B.10
C.15 D.20
A
2.如图,在△ABC中,点D,E分别是AB,AC的中点,有下列结论:
①BC=2DE;②△ADE∽△ABC;③=.其中正确结论的个数为( )
A.3 B.2
C.1 D.0
3.如图,在 ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F.
若AE=2DE,DC=3 cm,则AF的长为( )
A.5 cm B.6 cm
C.7 cm D.8 cm
B
△ABP∽△AED(答案不唯一)
4.如图,在 ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,
BP∥DF,且与AD相交于点P.请从图中找出一组相似的三角形:
.
5.如图,已知DF∥BC交AC于点E,CF∥AB.
求证:△ABC∽△CFE.
证明:∵DF∥BC,∴△ADE∽△ABC.
∵CF∥AB,∴△ADE∽△CFE,
∴△ABC∽△CFE.
小结
2. 当相似比等于 1 时,相似图形即是全等图形,全等是一种特殊的相似;
3. 平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1. 相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
第3章 图形的相似
3.4 相似三角形的判定
3.4.1 相似三角形的判定
第1课时 利用平行判定三角形相似
学习目标
1.了解相似三角形的判定方法,即平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
2.会用平行判定三角形相似.
复习导入
在八年级上册,我们已经探讨了两个三角形全等的条件,下面我们来
探讨两个三角形相似的条件.
为了研究满足什么条件的两个三角形相似,我们先来研究下述问题.
知识讲解
知识点1 相似三角形的性质及有关概念
我们就说 △ABC 与 △A′B′C′______,记作__________________,△ABC 与 △A′B′C′ 相似比是 k,则 △A′B′C′ 与 △ABC 的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在 △ABC 与 △A′B′C′ 中,如果∠A = ∠A′, ∠B = ∠B′,∠C = ∠C′,且===k,
△ABC∽△A′B′C′
相似
反之如果 △ABC∽△A′B′C′,则有∠A =_____,∠B =_____,∠C =____,且
∠A′
∠B′
∠C′
相似比为 1 时,相似的
两个图形有什么关系?
当相似比等于 1 时,相似图形是全等图形,全等是一种特殊的相似.
例1: △ABC 与 △DEF 的各角度数和边长如图所示,则 △ABC 与 △DEF 能否相似?说明理由.
解:因为∠A=70°,∠B=60°,所以∠C=50°.
因为∠F=60°,∠E=50°,所以∠D=70°.
所以∠A=∠D,∠B=∠F,∠C=∠E.
典例精析
∴ △ABC∽△DFE.
判断两个三角形相似,一定要具备两个条件:一是对应角相等,二是对应边成比例.另外在书写两个三角形相似时,一定要将对应的顶点写在对应的位置上.
方法总结
例2 :如图,已知 △ABC∽△ADE,AE=50 cm,EC=30 cm,BC=58 cm,∠BAC=45°,∠ACB=40°,求:
(1) ∠AED 和 ∠ADE 的度数;(2) DE 的长.
解:(1)∵△ABC∽△ADE,∴∠AED=∠ACB=40°.
在 △ADE 中,∠ADE=180°-40°-45°=95°.
(2) ∵△ABC∽△ADE.
∴ DE=36.25 cm.
当题目中有相似三角形(或能证明出相似三角形)时,首先考虑用相似三角形的性质,由性质既能得到相等的角,又能得到成比例的线段.
方法总结
知识点2 利用平行判定相似三角形
在△ABC 中,D为AB上任意一点,过点D作BC 的平行线DE,交AC于点E.
(1)△ADE 与△ABC 的三个角分别相等吗?
(2)分别度量△ADE与△ABC 的边长,它们的边长是否对应成比例?
(3)△ADE与△ABC之间有什么关系?平行移动DE 的位置,你的结论还成立吗?
我发现只要DE平行BC,那么三角形ADE与
三角形ABC是相似的.
A
B
C
D
下面我们来证明. 在 △ADE 与 △ABC 中,∠A = ∠A.
∵ DE∥BC,
∴∠ADE = ∠B, ∠AED = ∠C,
过 E 作 EF∥AB 交 BC 于 F,
F
E
∵四边形 DBFE 是平行四边形,
∴DE = BF.
∴△ADE∽△ABC.
A
B
C
D
F
E
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
归纳
例3: 如图,在△ABC 中,已知点 D,E 分别是 AB,AC边的中点. 求证:△ADE∽△ABC.
证明:∵点 D,E 分别是 AB,AC 边的中点,
∴ DE∥BC,
∴△ADE∽△ABC.
A
E
C
B
D
例4 :如图,点 D 作为△ABC 的边 AB 的中点,过点 D 作DE∥BC,交边 AC 于点 E.延长 DE 至点 F,使DE = EF.求证:△CFE∽△ABC.
解:∵DE∥BC,点 D 为△ABC 的边 AB 的中点,∴AE = CE.
又 DE = EF,∠AED = ∠CEF,
∴△ADE≌△CFE(SAS).
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
A
E
D
B
C
F
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
M
N
如果再作 MN∥DE ,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形
已知 DE∥BC,
交流讨论
如图,在 △ABC 中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果 AD = 1,DB = 3,那么 DG∶BC =_____.
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1∶4
练一练
随 堂 小 测
C
1.如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E.
若线段DE=5,则线段BC的长为( )
A.7.5 B.10
C.15 D.20
A
2.如图,在△ABC中,点D,E分别是AB,AC的中点,有下列结论:
①BC=2DE;②△ADE∽△ABC;③=.其中正确结论的个数为( )
A.3 B.2
C.1 D.0
3.如图,在 ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F.
若AE=2DE,DC=3 cm,则AF的长为( )
A.5 cm B.6 cm
C.7 cm D.8 cm
B
△ABP∽△AED(答案不唯一)
4.如图,在 ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,
BP∥DF,且与AD相交于点P.请从图中找出一组相似的三角形:
.
5.如图,已知DF∥BC交AC于点E,CF∥AB.
求证:△ABC∽△CFE.
证明:∵DF∥BC,∴△ADE∽△ABC.
∵CF∥AB,∴△ADE∽△CFE,
∴△ABC∽△CFE.
小结
2. 当相似比等于 1 时,相似图形即是全等图形,全等是一种特殊的相似;
3. 平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1. 相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
