3.4.2 第2课时 相似三角形对应周长和面积的性质 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.4.2 第2课时 相似三角形对应周长和面积的性质 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 594.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 15:00:20 | ||
图片预览





文档简介
(共18张PPT)
第3章 图形的相似
3.4 相似三角形的判定
3.4.2 相似三角形的性质
第2课时 相似三角形对应周长和面积的性质
学习目标
了解相似三角形的性质定理:“相似三角形的面积比等于相似比的平方”,并能运用这条定理解答几何中的计算问题.
情境导入
(1)如图,△ABC∽△A'B'C' ,相似比为2,△ABC与△A'B'C' 的周长比是多少? 面积比呢?
(2)如图,△ABC∽△A'B'C' ,相似比为k,△ABC与△A'B'C' 的周长比是多少? 面积比呢?
A
B
C
A′
B′
C′
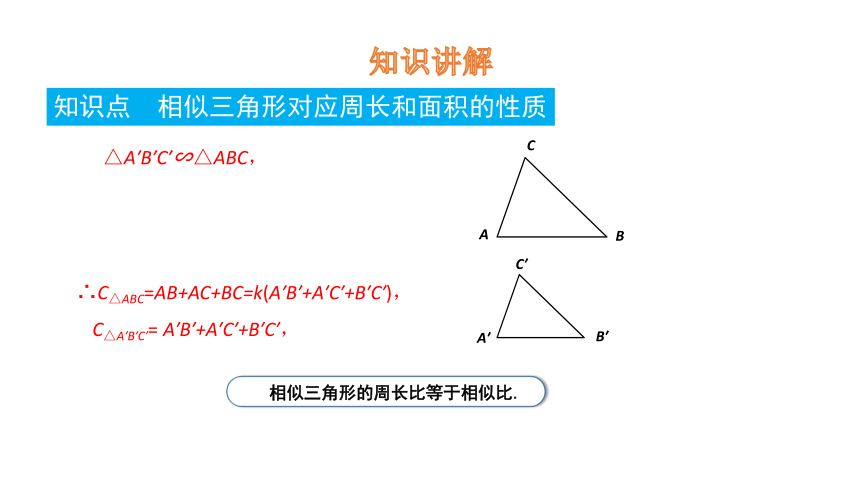
知识讲解
知识点 相似三角形对应周长和面积的性质
△A′B′C′∽△ABC,
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′),
C△A′B′C′= A′B′+A′C′+B′C′,
相似三角形的周长比等于相似比.
A
B
A′
B′
C′
C
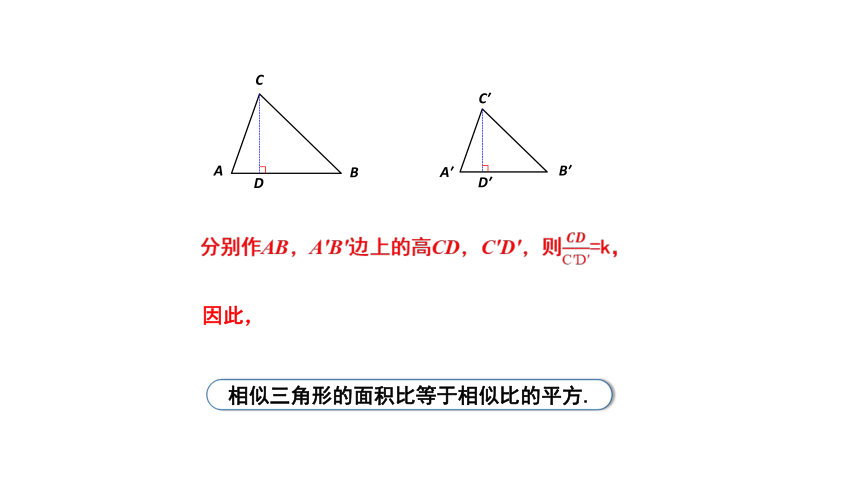
分别作AB,A′B′边上的高CD,C′D′,则=k,
因此,
相似三角形的面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
相似三角形的性质(2)
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
A
B
C
A′
B′
C′
1. 已知 △ABC 与 △A′B′C′ 的相似比为 2 : 3,则对应边上中线之比 ,面积之比为 .
2. 如果两个相似三角形的面积之比为 1 : 9,周长的比为______ .
1 : 3
2 : 3
4 : 9
练一练
典例精析
例1:如图所示,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2 ,且==,求四边形BCDE的面积.
∴△ABC ∽△ADE .
∴它们的相似比为53,面积比为25:9.
又∵△ABC的面积为100 cm2,
∴△ADE的面积为36 cm2 .
∴四边形BCDE的面积为100-36=64(cm2) .
解:∵∠BAD=∠DAE,且
,
B
A
E
D
C
A
B
C
D
E
F
例2:如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A =∠D. 若 △ABC 的边 BC 上的高为 6,面积为12 ,求 △DEF 的边 EF 上的高和面积.
解:在 △ABC 和 △DEF 中,
∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∴
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
A
B
C
D
E
F
例3:已知△ABC 与△A'B'C' 的相似比为,且 S△ABC + S△A'B'C' = 91,求△A'B'C' 的面积.
又∵ S△ABC + S△A'B'C' = 91,
解:∵△ABC 与△A'B'C' 的相似比为,
∴ S△A'B'C' = 63.
随 堂 小 测
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个四边形的面积也扩大为原来的 9 倍 ( )
√
×
2. 在 △ABC 和 △DEF 中,AB=2DE,AC=2DF,∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长为____cm,面积为 cm2.
14
____
5. 如图,这是圆桌正上方的灯泡 (点 A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米).
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,∴△ADF ∽△ACH.
A
D
E
F
C
B
H
A
D
E
F
C
B
H
∴ 即
解得 CH = 0.9 (米).
∴ 阴影部分的面积为
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
小结
相似三角形的性质 2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
第3章 图形的相似
3.4 相似三角形的判定
3.4.2 相似三角形的性质
第2课时 相似三角形对应周长和面积的性质
学习目标
了解相似三角形的性质定理:“相似三角形的面积比等于相似比的平方”,并能运用这条定理解答几何中的计算问题.
情境导入
(1)如图,△ABC∽△A'B'C' ,相似比为2,△ABC与△A'B'C' 的周长比是多少? 面积比呢?
(2)如图,△ABC∽△A'B'C' ,相似比为k,△ABC与△A'B'C' 的周长比是多少? 面积比呢?
A
B
C
A′
B′
C′
知识讲解
知识点 相似三角形对应周长和面积的性质
△A′B′C′∽△ABC,
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′),
C△A′B′C′= A′B′+A′C′+B′C′,
相似三角形的周长比等于相似比.
A
B
A′
B′
C′
C
分别作AB,A′B′边上的高CD,C′D′,则=k,
因此,
相似三角形的面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
相似三角形的性质(2)
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
A
B
C
A′
B′
C′
1. 已知 △ABC 与 △A′B′C′ 的相似比为 2 : 3,则对应边上中线之比 ,面积之比为 .
2. 如果两个相似三角形的面积之比为 1 : 9,周长的比为______ .
1 : 3
2 : 3
4 : 9
练一练
典例精析
例1:如图所示,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2 ,且==,求四边形BCDE的面积.
∴△ABC ∽△ADE .
∴它们的相似比为53,面积比为25:9.
又∵△ABC的面积为100 cm2,
∴△ADE的面积为36 cm2 .
∴四边形BCDE的面积为100-36=64(cm2) .
解:∵∠BAD=∠DAE,且
,
B
A
E
D
C
A
B
C
D
E
F
例2:如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A =∠D. 若 △ABC 的边 BC 上的高为 6,面积为12 ,求 △DEF 的边 EF 上的高和面积.
解:在 △ABC 和 △DEF 中,
∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∴
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
A
B
C
D
E
F
例3:已知△ABC 与△A'B'C' 的相似比为,且 S△ABC + S△A'B'C' = 91,求△A'B'C' 的面积.
又∵ S△ABC + S△A'B'C' = 91,
解:∵△ABC 与△A'B'C' 的相似比为,
∴ S△A'B'C' = 63.
随 堂 小 测
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个四边形的面积也扩大为原来的 9 倍 ( )
√
×
2. 在 △ABC 和 △DEF 中,AB=2DE,AC=2DF,∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_____.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长为____cm,面积为 cm2.
14
____
5. 如图,这是圆桌正上方的灯泡 (点 A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米).
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,∴△ADF ∽△ACH.
A
D
E
F
C
B
H
A
D
E
F
C
B
H
∴ 即
解得 CH = 0.9 (米).
∴ 阴影部分的面积为
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
小结
相似三角形的性质 2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
