3.6 第1课时 位似图形的概念及画法 课件(共21张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.6 第1课时 位似图形的概念及画法 课件(共21张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第3章 图形的相似
3.6 位似
第1课时 位似图形的概念及画法
学习目标
1.了解图形的位似,掌握位似图形的定义及其性质.
2.知道利用位似图形可以将一个图形放大或者缩小.
3.在平面直角坐标系中,探索并了解一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
新知导入
如何把一个图形放大或缩小?
下面我们来学习一种简单可行的方法.
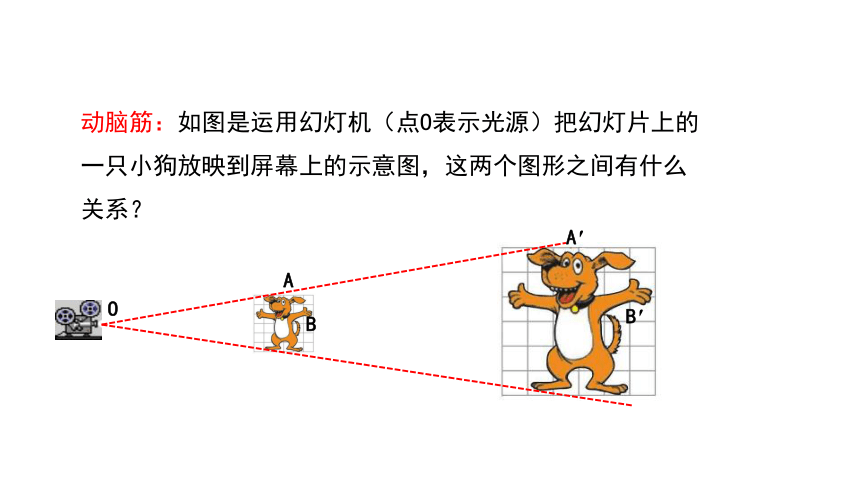
动脑筋:如图是运用幻灯机(点O表示光源)把幻灯片上的一只小狗放映到屏幕上的示意图,这两个图形之间有什么关系?
O
A
A'
B
B'
这两个图形的形状相同,但大小不同,它们是相似图形.
在上图中的左边小狗的头顶上和狗尾巴尖上分别取点A,B.右边小狗的头顶和
狗尾巴尖上的点A',B'分别为点A和点B的对应点.
此时我们会发现点A,A'与点O在一条直线上,点B,B'与点O也在一条直线上.
分别量出线段OA,OA',OB,OB'的长度,计算(精确到0.1):
= ,= .
继续在左、右两只小狗上找出一些对应点,我们会发现每一对对应点都与点O在
一条直线上,且每一对对应点与点O所连线段的比与上述,的值相等.
知识讲解
知识点1 位似的概念
一般地,取定一个点 O,如果一个图形 G 上每一个点 P 对应于另一图形 G′ 上的点 P′ ,且满足:
(1)直线 PP′ 都经过点 O,
(2)=|k|,其中 k 是非零常数,当 k>0 时,点 P′ 在射线 OP 上,当 k<0 时,点 P′ 在射线 OP 的反向延长线上.
那么称图形 G 与图形 G′ 是位似图形,这个点 O 叫作位似中心.常数 k 叫作位似比.
A
B
B'
A'
O
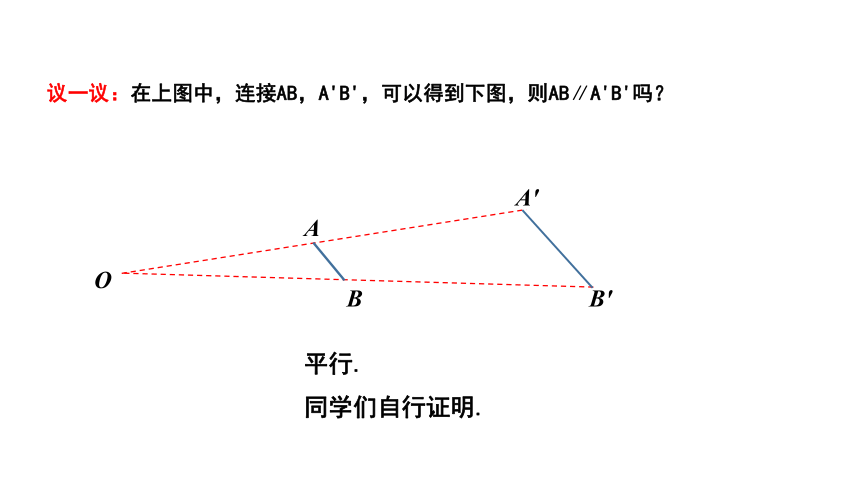
议一议:在上图中,连接AB,A'B',可以得到下图,则AB∥A'B'吗?
平行.
同学们自行证明.
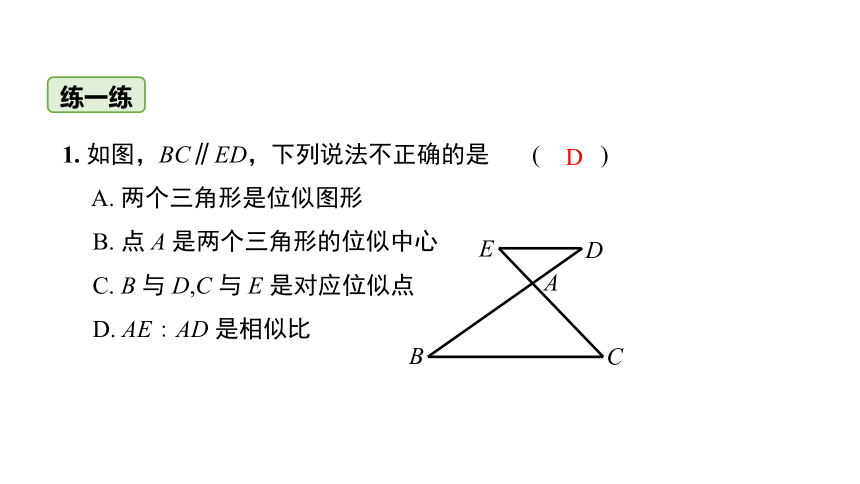
1. 如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D,C 与 E 是对应位似点
D. AE : AD 是相似比
D
D
E
A
B
C
练一练
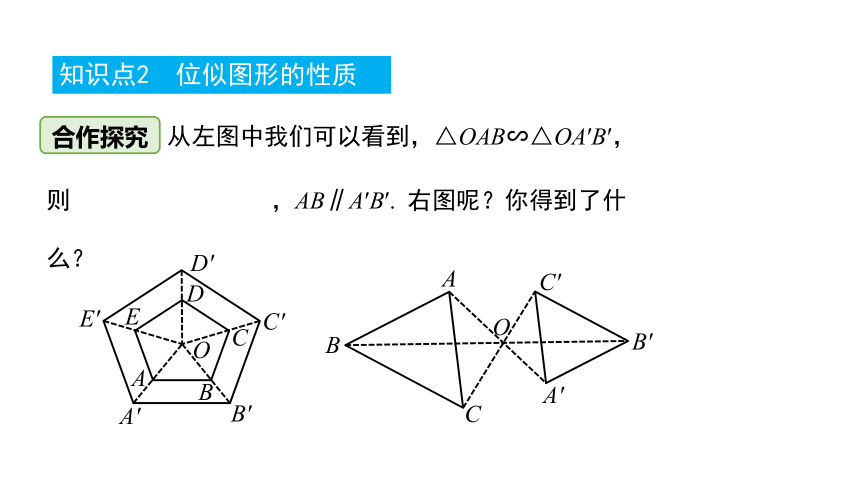
合作探究
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
知识点2 位似图形的性质
两个图形位似,则这两个图形不仅相似,而且对应点的连线相交于一点,对应边互相平行(或者在同一直线上).
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
利用位似,可以把一个图形进行放大或缩小.
归纳
如图,四边形木框 ABCD 在灯泡发出的光照射下形成的影子是四边形 A′B′C′D′,若 OB : OB′=1 : 2,则四边形 ABCD 的面积与四边形 A′B′C′D′ 的面积比为 ( )
A.4 : 1 B. : 1
C.1 : D.1 : 4
D
练一练
A′
A
C
C′
D′
灯泡
O
用以下方法可以近似地把一个不规则图形放大:
1.将两根等长的橡皮筋系在一起,连接处形成一个结点.
2.选一个图形,在图形外取一个定点.
3.将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端.
4.拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形.
这个新图形与已知图形形状相同.
请你用这种方法把一个已知图形放大.
知识点3 位似图形的画法
例1:如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD = 2OA,OE = 2OB,OF = 2OC;顺次连接D,E,F,使△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
问题:你还有其他的画法吗?
A
B
C
画法二:△ABC与△DEF异侧.
解:画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD = 2OA,OE = 2OB,
OF = 2OC;顺次连接D,E,F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
例2:已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法一:△ABC与△DEF在同侧.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺次连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
D
E
F
A
B
C
画法二: △ABC与△DEF在异侧.
解:画射线OA,OB,OC;在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,
OC = 2OF;顺次连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
D
F
E
画位似图形的关键是画出图形中顶点的对应点,画图的方法大致有两种:一是每对对应点都在位似中心的同侧,二是每对对应点在位似中心的异侧.
归纳
随 堂 小 测
A
B
C
D
1.选出下面不同于其他三组的图形( )
B
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若 AB : FG = 2 : 3,则下列结论正确的是 ( )
A. 2DE = 3MN B. 3DE = 2MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
3. 下列说法:
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形 ABCDE 与五边形 A′B′C′D′E′ 位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且相似比相等. 其中正确的有 .
①④
例如特殊情况:两个图形重叠或者不同的两点.
小结
定义
位似多边形及其性质
性质
如果两个相似多边形任意一组对应顶点P,
P 所在的直线都过同一点O,且OP =k· OP
(k≠0),那么这样的两个多边形叫做位似多边形
②对应点的连线相交于一点,对应边互相平行或在同一直线上
① 两个图形相似
③任意一对对应点到位似中心的距离之比等于相似比
作位似图形:关键是确定位似中心、相似比和找关键点的对应点.
第3章 图形的相似
3.6 位似
第1课时 位似图形的概念及画法
学习目标
1.了解图形的位似,掌握位似图形的定义及其性质.
2.知道利用位似图形可以将一个图形放大或者缩小.
3.在平面直角坐标系中,探索并了解一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
新知导入
如何把一个图形放大或缩小?
下面我们来学习一种简单可行的方法.
动脑筋:如图是运用幻灯机(点O表示光源)把幻灯片上的一只小狗放映到屏幕上的示意图,这两个图形之间有什么关系?
O
A
A'
B
B'
这两个图形的形状相同,但大小不同,它们是相似图形.
在上图中的左边小狗的头顶上和狗尾巴尖上分别取点A,B.右边小狗的头顶和
狗尾巴尖上的点A',B'分别为点A和点B的对应点.
此时我们会发现点A,A'与点O在一条直线上,点B,B'与点O也在一条直线上.
分别量出线段OA,OA',OB,OB'的长度,计算(精确到0.1):
= ,= .
继续在左、右两只小狗上找出一些对应点,我们会发现每一对对应点都与点O在
一条直线上,且每一对对应点与点O所连线段的比与上述,的值相等.
知识讲解
知识点1 位似的概念
一般地,取定一个点 O,如果一个图形 G 上每一个点 P 对应于另一图形 G′ 上的点 P′ ,且满足:
(1)直线 PP′ 都经过点 O,
(2)=|k|,其中 k 是非零常数,当 k>0 时,点 P′ 在射线 OP 上,当 k<0 时,点 P′ 在射线 OP 的反向延长线上.
那么称图形 G 与图形 G′ 是位似图形,这个点 O 叫作位似中心.常数 k 叫作位似比.
A
B
B'
A'
O
议一议:在上图中,连接AB,A'B',可以得到下图,则AB∥A'B'吗?
平行.
同学们自行证明.
1. 如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D,C 与 E 是对应位似点
D. AE : AD 是相似比
D
D
E
A
B
C
练一练
合作探究
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
知识点2 位似图形的性质
两个图形位似,则这两个图形不仅相似,而且对应点的连线相交于一点,对应边互相平行(或者在同一直线上).
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
利用位似,可以把一个图形进行放大或缩小.
归纳
如图,四边形木框 ABCD 在灯泡发出的光照射下形成的影子是四边形 A′B′C′D′,若 OB : OB′=1 : 2,则四边形 ABCD 的面积与四边形 A′B′C′D′ 的面积比为 ( )
A.4 : 1 B. : 1
C.1 : D.1 : 4
D
练一练
A′
A
C
C′
D′
灯泡
O
用以下方法可以近似地把一个不规则图形放大:
1.将两根等长的橡皮筋系在一起,连接处形成一个结点.
2.选一个图形,在图形外取一个定点.
3.将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端.
4.拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形.
这个新图形与已知图形形状相同.
请你用这种方法把一个已知图形放大.
知识点3 位似图形的画法
例1:如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD = 2OA,OE = 2OB,OF = 2OC;顺次连接D,E,F,使△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
问题:你还有其他的画法吗?
A
B
C
画法二:△ABC与△DEF异侧.
解:画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD = 2OA,OE = 2OB,
OF = 2OC;顺次连接D,E,F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
例2:已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法一:△ABC与△DEF在同侧.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺次连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
D
E
F
A
B
C
画法二: △ABC与△DEF在异侧.
解:画射线OA,OB,OC;在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,
OC = 2OF;顺次连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
D
F
E
画位似图形的关键是画出图形中顶点的对应点,画图的方法大致有两种:一是每对对应点都在位似中心的同侧,二是每对对应点在位似中心的异侧.
归纳
随 堂 小 测
A
B
C
D
1.选出下面不同于其他三组的图形( )
B
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若 AB : FG = 2 : 3,则下列结论正确的是 ( )
A. 2DE = 3MN B. 3DE = 2MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
3. 下列说法:
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形 ABCDE 与五边形 A′B′C′D′E′ 位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且相似比相等. 其中正确的有 .
①④
例如特殊情况:两个图形重叠或者不同的两点.
小结
定义
位似多边形及其性质
性质
如果两个相似多边形任意一组对应顶点P,
P 所在的直线都过同一点O,且OP =k· OP
(k≠0),那么这样的两个多边形叫做位似多边形
②对应点的连线相交于一点,对应边互相平行或在同一直线上
① 两个图形相似
③任意一对对应点到位似中心的距离之比等于相似比
作位似图形:关键是确定位似中心、相似比和找关键点的对应点.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
