4.1 第1课时 正弦 课件(共21张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 4.1 第1课时 正弦 课件(共21张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 15:04:09 | ||
图片预览







文档简介
(共21张PPT)
第4章 锐角三角函数
4.1 正弦和余弦
第1课时 正弦
学习目标
1.利用相似直角三角形,探索并认识锐角三角函数(sin A)的定义.
2.会根据已知直角三角形的边长求一个锐角的正弦值.
新课导入
北
东
30
A
B
C
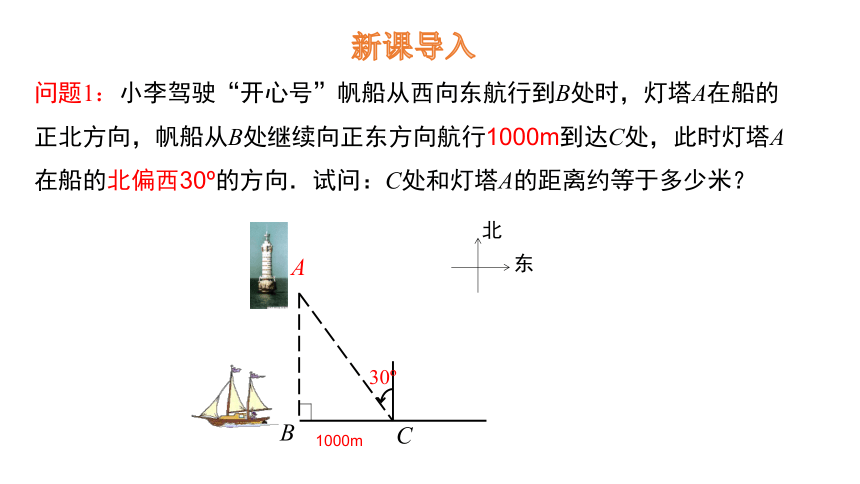
问题1:小李驾驶“开心号”帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行1000m到达C处,此时灯塔A在船的北偏西30 的方向.试问:C处和灯塔A的距离约等于多少米?
1000m
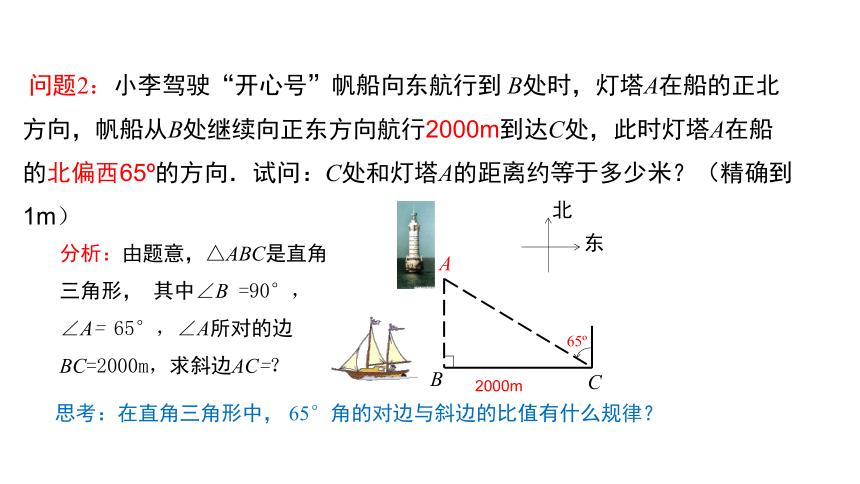
分析:由题意,△ABC是直角三角形, 其中∠B =90°,∠A= 65°,∠A所对的边BC=2000m,求斜边AC=?
北
东
思考:在直角三角形中, 65°角的对边与斜边的比值有什么规律?
65
A
B
C
问题2:小李驾驶“开心号”帆船向东航行到 B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
2000m
知识讲解
知识点 正弦
做一做:每位同学画一个直角三角形,其中一个锐角为65°,量出65 角的对边长度和斜边长度,计算:
的值(精确到0.01)
结论:在有一个锐角为65 的直角三角形中, 65 角的对边与斜边的比值是一个常数,它约等于0.91.
与同桌和邻桌的同学交流,你能发现什么?
猜想:在有一个锐角为 的所有直角三角形中,角 的对边与斜边的比值一定是一个常数吗?
证明:∵ ∠C=∠F=90°,∠A=∠D,
∴ △ABC ∽ △DEF.
已知:任意两个直角三角形△ABC 和△DEF,∠C=∠F = 90 ,∠A =∠D.
E
F
D
B
C
A
验证猜想
结论:在有一个锐角为 的所有直角三角形中,角 的对边与斜边的比值一定是一个常数.
解决问题:现在解决第2题中,帆船航行到C处时和灯塔A的距离约等于多少米的问题.
解:在直角三角形ABC中,BC=2000m ,∠A= 65 ,
解得
答:C 处和灯塔A的距离约等于2200米.
在直角三角形中,锐角α的对边与斜边的比叫做角α的正弦,记作sin α,
即sin α=.
B
C
A
a
(1)sinA 不是一个角
(2)sinA 不是sin与A的乘积
(3)sinA 是一个比值
(4)sinA 没有单位
例1.如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
典例精析
例2. 在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100
倍,sin A 的值 ( )
A. 扩大 100 倍 B. 缩小
C. 不变 D. 不能确定
C
(2)∠B 的对边是 AC,根据勾股定理,得 AC2 = AB2 - BC2 = 52 - 32 = 16.于是 AC = 4.因此sin B==.
例3: 如图,在 Rt△ABC 中,∠C = 90°,BC = 3,AC = 5.
(1)求 sin A 的值;
(2)求 sin B 的值.
A
B
C
5
3
解:(1)∠A 的对边BC = 3,斜边AB = 5,于是sin A==.
例4:如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
解:如图,过点 P 作 PA⊥x 轴于点 A,则点 A (3,0),AP = 4.
A (3,0)
在 Rt△APO 中,由勾股定理得
因此
α
方法总结:结合平面直角坐标系求某角的正弦函数值,一般过已知点向 x 轴或 y 轴作垂线,构造直角三角形,再结合勾股定理求解.
例5:如图,在 Rt△ABC 中,∠C = 90°,sin A=,BC = 3,求 sin B 及 Rt△ABC 的面积.
A
B
C
提示:已知 sin A 及∠A 的对边 BC 的长度,可以求出斜边 AB 的长,然后再利用勾股定理,求出 AC 的长度,进而求出
sin B 及 Rt△ABC 的面积.
解:∵∠C = 90°, ∴
∴ AB = 3BC = 3×3 = 9.
∴
∴
∴
随 堂 小 测
1. 在直角三角形 ABC 中,若三边长都扩大为原来的 2 倍,则锐角 A 的正弦值将 ( )
A. 扩大为原来的 2 倍 B.不变
C. 缩小为原来的 D. 无法确定
B
2. 如图,在正方形网格中有 △ABC,则 sin∠ABC 的值为 .
解析:∵ AB= ,BC= ,AC= ,∴ AB2=BC2+AC2.
∴ ∠ACB=90°.
∴ sin∠ABC=
3. 如图,在 △ABC 中, AB = BC = 5,sinA =,求△ABC 的面积.
D
5
5
C
B
A
解:作 BD⊥AC 于点 D.
∵ sin A = ,
∴
又∵ AB = AC,BD⊥AC,∴ AC = 2AD = 6,
∴ S△ABC = AC · BD÷2 = 12.
小结
正弦的概念
正弦
正弦的应用
∠A的对边
斜边
sin A =
已知边长求正弦值
已知正弦值求边长
第4章 锐角三角函数
4.1 正弦和余弦
第1课时 正弦
学习目标
1.利用相似直角三角形,探索并认识锐角三角函数(sin A)的定义.
2.会根据已知直角三角形的边长求一个锐角的正弦值.
新课导入
北
东
30
A
B
C
问题1:小李驾驶“开心号”帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行1000m到达C处,此时灯塔A在船的北偏西30 的方向.试问:C处和灯塔A的距离约等于多少米?
1000m
分析:由题意,△ABC是直角三角形, 其中∠B =90°,∠A= 65°,∠A所对的边BC=2000m,求斜边AC=?
北
东
思考:在直角三角形中, 65°角的对边与斜边的比值有什么规律?
65
A
B
C
问题2:小李驾驶“开心号”帆船向东航行到 B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
2000m
知识讲解
知识点 正弦
做一做:每位同学画一个直角三角形,其中一个锐角为65°,量出65 角的对边长度和斜边长度,计算:
的值(精确到0.01)
结论:在有一个锐角为65 的直角三角形中, 65 角的对边与斜边的比值是一个常数,它约等于0.91.
与同桌和邻桌的同学交流,你能发现什么?
猜想:在有一个锐角为 的所有直角三角形中,角 的对边与斜边的比值一定是一个常数吗?
证明:∵ ∠C=∠F=90°,∠A=∠D,
∴ △ABC ∽ △DEF.
已知:任意两个直角三角形△ABC 和△DEF,∠C=∠F = 90 ,∠A =∠D.
E
F
D
B
C
A
验证猜想
结论:在有一个锐角为 的所有直角三角形中,角 的对边与斜边的比值一定是一个常数.
解决问题:现在解决第2题中,帆船航行到C处时和灯塔A的距离约等于多少米的问题.
解:在直角三角形ABC中,BC=2000m ,∠A= 65 ,
解得
答:C 处和灯塔A的距离约等于2200米.
在直角三角形中,锐角α的对边与斜边的比叫做角α的正弦,记作sin α,
即sin α=.
B
C
A
a
(1)sinA 不是一个角
(2)sinA 不是sin与A的乘积
(3)sinA 是一个比值
(4)sinA 没有单位
例1.如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
典例精析
例2. 在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100
倍,sin A 的值 ( )
A. 扩大 100 倍 B. 缩小
C. 不变 D. 不能确定
C
(2)∠B 的对边是 AC,根据勾股定理,得 AC2 = AB2 - BC2 = 52 - 32 = 16.于是 AC = 4.因此sin B==.
例3: 如图,在 Rt△ABC 中,∠C = 90°,BC = 3,AC = 5.
(1)求 sin A 的值;
(2)求 sin B 的值.
A
B
C
5
3
解:(1)∠A 的对边BC = 3,斜边AB = 5,于是sin A==.
例4:如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
解:如图,过点 P 作 PA⊥x 轴于点 A,则点 A (3,0),AP = 4.
A (3,0)
在 Rt△APO 中,由勾股定理得
因此
α
方法总结:结合平面直角坐标系求某角的正弦函数值,一般过已知点向 x 轴或 y 轴作垂线,构造直角三角形,再结合勾股定理求解.
例5:如图,在 Rt△ABC 中,∠C = 90°,sin A=,BC = 3,求 sin B 及 Rt△ABC 的面积.
A
B
C
提示:已知 sin A 及∠A 的对边 BC 的长度,可以求出斜边 AB 的长,然后再利用勾股定理,求出 AC 的长度,进而求出
sin B 及 Rt△ABC 的面积.
解:∵∠C = 90°, ∴
∴ AB = 3BC = 3×3 = 9.
∴
∴
∴
随 堂 小 测
1. 在直角三角形 ABC 中,若三边长都扩大为原来的 2 倍,则锐角 A 的正弦值将 ( )
A. 扩大为原来的 2 倍 B.不变
C. 缩小为原来的 D. 无法确定
B
2. 如图,在正方形网格中有 △ABC,则 sin∠ABC 的值为 .
解析:∵ AB= ,BC= ,AC= ,∴ AB2=BC2+AC2.
∴ ∠ACB=90°.
∴ sin∠ABC=
3. 如图,在 △ABC 中, AB = BC = 5,sinA =,求△ABC 的面积.
D
5
5
C
B
A
解:作 BD⊥AC 于点 D.
∵ sin A = ,
∴
又∵ AB = AC,BD⊥AC,∴ AC = 2AD = 6,
∴ S△ABC = AC · BD÷2 = 12.
小结
正弦的概念
正弦
正弦的应用
∠A的对边
斜边
sin A =
已知边长求正弦值
已知正弦值求边长
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
