4.1 第3课时 余弦 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 4.1 第3课时 余弦 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 946.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 15:04:21 | ||
图片预览





文档简介
(共18张PPT)
第4章 锐角三角函数
4.1 正弦和余弦
第3课时 余弦
学习目标
1.会利用相似直角三角形探索并认识余弦的定义.
2.会求特殊角30°,45°,60°的余弦值并熟记这些值.
3.会用计算器求锐角的余弦值以及根据余弦值求对应锐角.
新知导入
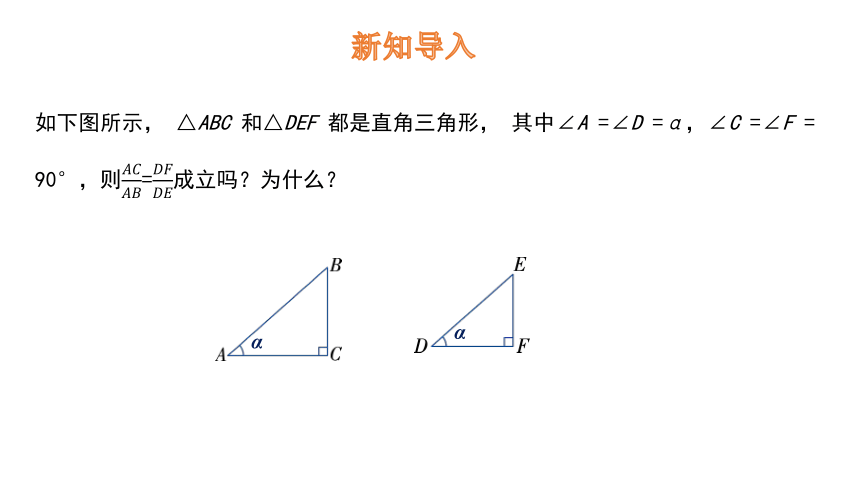
如下图所示, △ABC 和△DEF 都是直角三角形, 其中∠A =∠D =α,∠C =∠F = 90°,则=成立吗?为什么?
知识讲解
知识点1 余弦
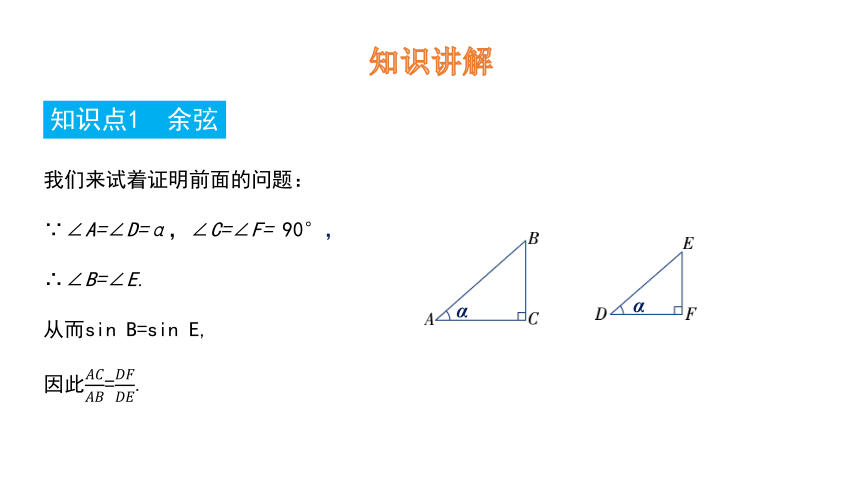
我们来试着证明前面的问题:
∵∠A=∠D=α,∠C=∠F= 90°,
∴∠B=∠E.
从而sin B=sin E,
因此=.
在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,
记作cos α,
这证明了:在有一个锐角等于α的所有直角三角形中,角α的邻边与斜边的比值等于角(90°-α)的对边与斜边的比值.
根据上述证明过程看出:对于任意锐角α,有
定义
从上述探究和证明过程看出,对于任意锐角α,
有
cosα=sin (90°-α),
从而有
sinα=cos (90°-α).
解:cos 30°=sin(90°-30°)=sin 60°,
cos 45°=sin(90°-45°)=sin 45°,
cos 60°=sin(90°-60°)=sin 45°.
典例精析
例1 cos 30°,cos 45°,cos 60°.
例2 计算:cos 30°-cos 60°+cos245°.
解:原式
=-×+×
=.
例3 如图,△ABC中,∠C=90°,AB=8,cosA=,则AC和BC的长是多少?并求sinA的值.
解: AC 和BC 的长分别是6,
sinA的值为 .
知识点2 用计算器求锐角的余弦或根据余弦值求锐角
对于一般锐角α(30°,45°,60°除外)的余弦值,我们可以用计算器来求.
例如求50°角的余弦值,可在计算器上依次按键 ,显示结果为 0.6427….
如果已知余弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知 cosα = 0.8661,依次按键 ,显示结果为29.9914…,表示角α约等于30°.
随 堂 小 测
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A = 35°,则直角边 BC 的长是 ( )
A.msin35°
B.mcos 35°
C.
D.
A
A
B
C
2. 随着锐角 α 的增大,cos α 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
B
当 0°<α<90° 时,cos α 的值随着角度的增大 (或减小) 而减小 (或增大)
3.如图,在 Rt△ABC 中,锐角 A 的对边和邻边同时扩大100 倍,sin A 的值( )
A. 扩大 100 倍 B. 缩小 100 倍
C. 不变 D. 不能确定
A
B
C
┌
C
4.已知∠A,∠B 为锐角,
(1)若∠A = ∠B,则 sin A sin B;
(2)若 sin A = sin B,则∠A ∠B.
=
=
5. 如图,在平面直角坐标系内,O 为原点,点 A 的坐标为(10,0),点 B 在第一象限内,BO = 5,sin∠BOA=.
(1)求点 B 的坐标;
(2)求 cos∠BAO 的值.
A
B
H
解:(1)如图所示,作 BH⊥OA, 垂足为 H.在 Rt△OHB 中,
∵BO=5,sin∠BOA=,
∴BH=3,OH=4,
∴点 B 的坐标为(4,3).
5.如图,在平面直角坐标系内,O 为原点,点 A 的坐标为(10,0),点 B 在第一象限内,BO = 5,sin∠BOA=.
(2)求 cos∠BAO 的值.
(2)∵ OA=10,OH=4,∴ AH=6.
∵在 Rt△AHB 中,BH=3,
A
B
H
小结
余弦
余弦的概念:在直角三角形中,锐角α 的邻边与斜边的比叫作角 α 的余弦
余弦的性质:α 确定的情况下,cos α为定值,与三角形的大小无关
用计算器求锐角余弦值或根据余弦值求锐角
第4章 锐角三角函数
4.1 正弦和余弦
第3课时 余弦
学习目标
1.会利用相似直角三角形探索并认识余弦的定义.
2.会求特殊角30°,45°,60°的余弦值并熟记这些值.
3.会用计算器求锐角的余弦值以及根据余弦值求对应锐角.
新知导入
如下图所示, △ABC 和△DEF 都是直角三角形, 其中∠A =∠D =α,∠C =∠F = 90°,则=成立吗?为什么?
知识讲解
知识点1 余弦
我们来试着证明前面的问题:
∵∠A=∠D=α,∠C=∠F= 90°,
∴∠B=∠E.
从而sin B=sin E,
因此=.
在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,
记作cos α,
这证明了:在有一个锐角等于α的所有直角三角形中,角α的邻边与斜边的比值等于角(90°-α)的对边与斜边的比值.
根据上述证明过程看出:对于任意锐角α,有
定义
从上述探究和证明过程看出,对于任意锐角α,
有
cosα=sin (90°-α),
从而有
sinα=cos (90°-α).
解:cos 30°=sin(90°-30°)=sin 60°,
cos 45°=sin(90°-45°)=sin 45°,
cos 60°=sin(90°-60°)=sin 45°.
典例精析
例1 cos 30°,cos 45°,cos 60°.
例2 计算:cos 30°-cos 60°+cos245°.
解:原式
=-×+×
=.
例3 如图,△ABC中,∠C=90°,AB=8,cosA=,则AC和BC的长是多少?并求sinA的值.
解: AC 和BC 的长分别是6,
sinA的值为 .
知识点2 用计算器求锐角的余弦或根据余弦值求锐角
对于一般锐角α(30°,45°,60°除外)的余弦值,我们可以用计算器来求.
例如求50°角的余弦值,可在计算器上依次按键 ,显示结果为 0.6427….
如果已知余弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知 cosα = 0.8661,依次按键 ,显示结果为29.9914…,表示角α约等于30°.
随 堂 小 测
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A = 35°,则直角边 BC 的长是 ( )
A.msin35°
B.mcos 35°
C.
D.
A
A
B
C
2. 随着锐角 α 的增大,cos α 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
B
当 0°<α<90° 时,cos α 的值随着角度的增大 (或减小) 而减小 (或增大)
3.如图,在 Rt△ABC 中,锐角 A 的对边和邻边同时扩大100 倍,sin A 的值( )
A. 扩大 100 倍 B. 缩小 100 倍
C. 不变 D. 不能确定
A
B
C
┌
C
4.已知∠A,∠B 为锐角,
(1)若∠A = ∠B,则 sin A sin B;
(2)若 sin A = sin B,则∠A ∠B.
=
=
5. 如图,在平面直角坐标系内,O 为原点,点 A 的坐标为(10,0),点 B 在第一象限内,BO = 5,sin∠BOA=.
(1)求点 B 的坐标;
(2)求 cos∠BAO 的值.
A
B
H
解:(1)如图所示,作 BH⊥OA, 垂足为 H.在 Rt△OHB 中,
∵BO=5,sin∠BOA=,
∴BH=3,OH=4,
∴点 B 的坐标为(4,3).
5.如图,在平面直角坐标系内,O 为原点,点 A 的坐标为(10,0),点 B 在第一象限内,BO = 5,sin∠BOA=.
(2)求 cos∠BAO 的值.
(2)∵ OA=10,OH=4,∴ AH=6.
∵在 Rt△AHB 中,BH=3,
A
B
H
小结
余弦
余弦的概念:在直角三角形中,锐角α 的邻边与斜边的比叫作角 α 的余弦
余弦的性质:α 确定的情况下,cos α为定值,与三角形的大小无关
用计算器求锐角余弦值或根据余弦值求锐角
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
