3.5 相似三角形的应用 课件(共27张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 3.5 相似三角形的应用 课件(共27张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
第3章 图形的相似
3.5 相似三角形的应用
学习目标
会利用图形的相似解决一些简单的实际问题.
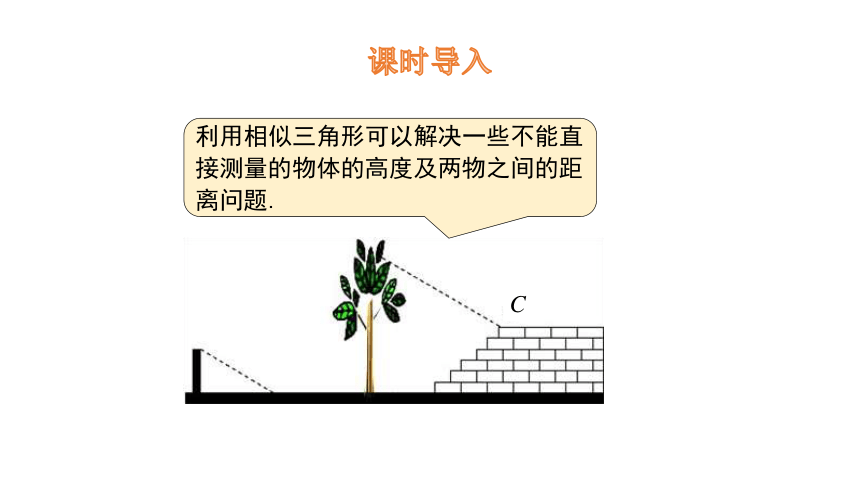
课时导入
C
利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.
知识讲解
知识点 相似三角形的应用
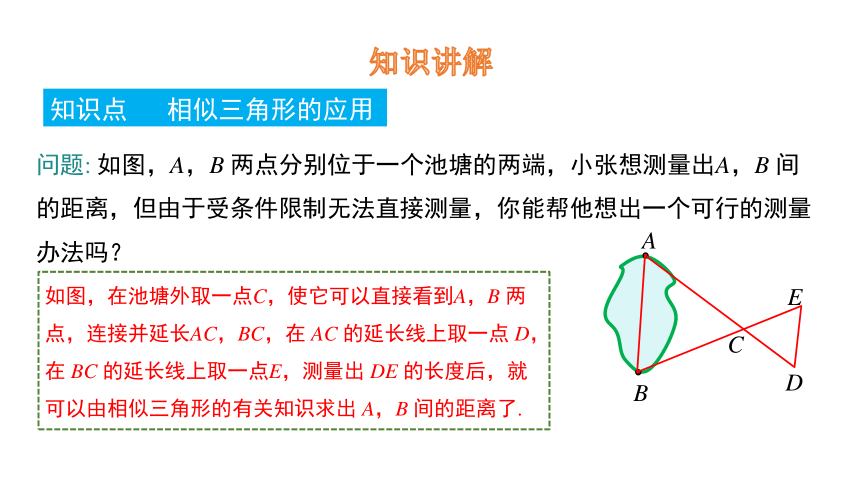
问题: 如图,A,B 两点分别位于一个池塘的两端,小张想测量出A,B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
A
B
如图,在池塘外取一点C,使它可以直接看到A,B 两点,连接并延长AC,BC,在 AC 的延长线上取一点 D,在 BC 的延长线上取一点E,测量出 DE 的长度后,就可以由相似三角形的有关知识求出 A,B 间的距离了.
C
D
E
典例分析
例1:某校数学兴趣小组为测量学校旗杆AC的高度, 在点F处竖立一根长为1.5米的标杆DF, 如图所示, 测得标杆的影长EF=1米,旗杆的影长BC=6米, 那么旗杆AC的高度是多少?
解:依题意,得DF∥AC.
又因为DE∥AB, 所以△ABC∽△DEF,
所以,即=,解得AC=9.
所以旗杆AC 的高度为9米.
解法归纳
利用太阳光测量物体高度的方法
在同一时刻, 同一地点, 物高与影长成比例,即=.
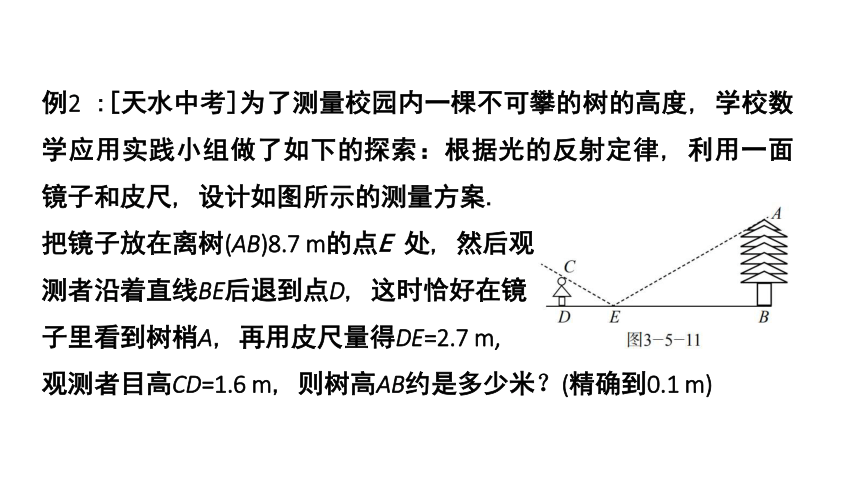
例2 :[天水中考]为了测量校园内一棵不可攀的树的高度, 学校数学应用实践小组做了如下的探索:根据光的反射定律, 利用一面镜子和皮尺, 设计如图所示的测量方案.
把镜子放在离树(AB)8.7 m的点E 处, 然后观
测者沿着直线BE后退到点D, 这时恰好在镜
子里看到树梢A, 再用皮尺量得DE=2.7 m,
观测者目高CD=1.6 m, 则树高AB约是多少米?(精确到0.1 m)
分析:由图可知CD⊥DE, AB⊥BE, 即∠CDE=∠ABE=90°. 由光的反射原理可知∠CED=∠AEB,由此可以得到△CED∽△AEB, 然后利用相似三角形的对应边成比例就可以求出AB的长.
解:由题意知∠CDE=∠ABE=90°,
又由光的反射原理可知∠CED=∠AEB,
∴△CED∽△AEB,
解得AB≈5.2.故树高AB约是5.2 m.
解法归纳
利用镜子的反射测量物体高度的方法
被测物体的高度可通过判定两个三角形相似, 然后利用相似三角形的对应边成比例求得.而判定两个三角形相似时, 一般是找两个角相等, 即两个直角相等(被测物体和人都垂直于地面), 两个锐角相等(由入射角等于反射角求得).
例3:[菏泽中考]如图, M, N为山两侧的两个村庄, 为了两村交通方便, 根据国家的惠民政策, 政府决定打一直线涵洞.工程人员为了计算工程量, 必须计算M,N两点之间的直线距离,选择测量点A, B, C, 点B,C分别在AM, AN上, 现测得AM=1千米,AN=1.8千米, AB=54米, BC=45米, AC=30米, 求M, N两点之间的直线距离.
分析 :先根据相似三角形的判定定理得出△ ABC与△AMN相似, 再利用相似三角形的性质解答即可.
解 :连接MN. 在△ABC和△AMN中,
∠A=∠A,
∴△ABC∽△ANM,
∴=,即=,
解得MN=1500(米)=1.5(千米).
答:M, N两点之间的直线距离是1.5千米.
解题归纳
测量地面上不能直接到达的两点间的距离的方法
对于实际问题中不能直接测量的两点间的距离, 可通过构造相似三角形, 利用相似三角形的对应边成比例间接求解.
例4:如图所示, 王刚同学所在的学习小组欲测量校园里一棵大树的高度, 他们选王刚作为观测者, 并在王刚与大树之间的地面上直立一根高为2m的标杆CD, 然后, 王刚开始调整自己的位置, 当他看到标杆的顶端C与树的顶端E 重合时, 就在该位置停止不
动, 这时其他同学通过测量,发现王刚的脚离标杆底部
的距离BD为1 m, 离大树底部的距离BF为9 m, 王刚的眼
睛离地面的高度AB为1.5 m,
那么大树EF的高为多少?
解:过点A作AG⊥EF, 垂足为G, 交CD于点H,则AG=BF.
∵AB∥CD∥EF,∴CD⊥AG,∴AB=HD=GF.
∵AB=1.5 m, CD=2 m, BD=1 m,
∴CH=CD-HD=2-1.5=0.5(m), AH=BD=1m, AG=BF=9 m.
∵CD∥EF,∴△ACH∽△AEG,
∴=即=,
解得EG=4.5,
∴EF=EG+GF=4.5+1.5=6(m).
故大树EF的高为6 m.
解题归纳
利用标杆测物高
先把实际问题转化为数学问题, 找到相似三角形, 再利用相似三角形的对应边成比例列出比例式, 求出某条线段的长度, 进而得到所要求的物体的高度.
随 堂 小 测
C
B
A
C
小结
利用相似三角形测量高度
相似三角形的应用举例
利用相似三角形测量宽度
利用相似三角形解决有遮挡物问题
第3章 图形的相似
3.5 相似三角形的应用
学习目标
会利用图形的相似解决一些简单的实际问题.
课时导入
C
利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.
知识讲解
知识点 相似三角形的应用
问题: 如图,A,B 两点分别位于一个池塘的两端,小张想测量出A,B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
A
B
如图,在池塘外取一点C,使它可以直接看到A,B 两点,连接并延长AC,BC,在 AC 的延长线上取一点 D,在 BC 的延长线上取一点E,测量出 DE 的长度后,就可以由相似三角形的有关知识求出 A,B 间的距离了.
C
D
E
典例分析
例1:某校数学兴趣小组为测量学校旗杆AC的高度, 在点F处竖立一根长为1.5米的标杆DF, 如图所示, 测得标杆的影长EF=1米,旗杆的影长BC=6米, 那么旗杆AC的高度是多少?
解:依题意,得DF∥AC.
又因为DE∥AB, 所以△ABC∽△DEF,
所以,即=,解得AC=9.
所以旗杆AC 的高度为9米.
解法归纳
利用太阳光测量物体高度的方法
在同一时刻, 同一地点, 物高与影长成比例,即=.
例2 :[天水中考]为了测量校园内一棵不可攀的树的高度, 学校数学应用实践小组做了如下的探索:根据光的反射定律, 利用一面镜子和皮尺, 设计如图所示的测量方案.
把镜子放在离树(AB)8.7 m的点E 处, 然后观
测者沿着直线BE后退到点D, 这时恰好在镜
子里看到树梢A, 再用皮尺量得DE=2.7 m,
观测者目高CD=1.6 m, 则树高AB约是多少米?(精确到0.1 m)
分析:由图可知CD⊥DE, AB⊥BE, 即∠CDE=∠ABE=90°. 由光的反射原理可知∠CED=∠AEB,由此可以得到△CED∽△AEB, 然后利用相似三角形的对应边成比例就可以求出AB的长.
解:由题意知∠CDE=∠ABE=90°,
又由光的反射原理可知∠CED=∠AEB,
∴△CED∽△AEB,
解得AB≈5.2.故树高AB约是5.2 m.
解法归纳
利用镜子的反射测量物体高度的方法
被测物体的高度可通过判定两个三角形相似, 然后利用相似三角形的对应边成比例求得.而判定两个三角形相似时, 一般是找两个角相等, 即两个直角相等(被测物体和人都垂直于地面), 两个锐角相等(由入射角等于反射角求得).
例3:[菏泽中考]如图, M, N为山两侧的两个村庄, 为了两村交通方便, 根据国家的惠民政策, 政府决定打一直线涵洞.工程人员为了计算工程量, 必须计算M,N两点之间的直线距离,选择测量点A, B, C, 点B,C分别在AM, AN上, 现测得AM=1千米,AN=1.8千米, AB=54米, BC=45米, AC=30米, 求M, N两点之间的直线距离.
分析 :先根据相似三角形的判定定理得出△ ABC与△AMN相似, 再利用相似三角形的性质解答即可.
解 :连接MN. 在△ABC和△AMN中,
∠A=∠A,
∴△ABC∽△ANM,
∴=,即=,
解得MN=1500(米)=1.5(千米).
答:M, N两点之间的直线距离是1.5千米.
解题归纳
测量地面上不能直接到达的两点间的距离的方法
对于实际问题中不能直接测量的两点间的距离, 可通过构造相似三角形, 利用相似三角形的对应边成比例间接求解.
例4:如图所示, 王刚同学所在的学习小组欲测量校园里一棵大树的高度, 他们选王刚作为观测者, 并在王刚与大树之间的地面上直立一根高为2m的标杆CD, 然后, 王刚开始调整自己的位置, 当他看到标杆的顶端C与树的顶端E 重合时, 就在该位置停止不
动, 这时其他同学通过测量,发现王刚的脚离标杆底部
的距离BD为1 m, 离大树底部的距离BF为9 m, 王刚的眼
睛离地面的高度AB为1.5 m,
那么大树EF的高为多少?
解:过点A作AG⊥EF, 垂足为G, 交CD于点H,则AG=BF.
∵AB∥CD∥EF,∴CD⊥AG,∴AB=HD=GF.
∵AB=1.5 m, CD=2 m, BD=1 m,
∴CH=CD-HD=2-1.5=0.5(m), AH=BD=1m, AG=BF=9 m.
∵CD∥EF,∴△ACH∽△AEG,
∴=即=,
解得EG=4.5,
∴EF=EG+GF=4.5+1.5=6(m).
故大树EF的高为6 m.
解题归纳
利用标杆测物高
先把实际问题转化为数学问题, 找到相似三角形, 再利用相似三角形的对应边成比例列出比例式, 求出某条线段的长度, 进而得到所要求的物体的高度.
随 堂 小 测
C
B
A
C
小结
利用相似三角形测量高度
相似三角形的应用举例
利用相似三角形测量宽度
利用相似三角形解决有遮挡物问题
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
