5.1 总体平均数与方差的估计 课件(共23张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 5.1 总体平均数与方差的估计 课件(共23张PPT) 2023-2024学年数学湘教版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1018.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 15:06:32 | ||
图片预览








文档简介
(共23张PPT)
第5章 用样本推断总体
5.1 总体平均数与方差的估计
学习目标
1.在理解样本与总体的关系的基础上,认识并体会统计估计的意义、实施方法及在实际问题中的应用.
2.知道可以通过样本平均数、样本方差推断总体平均数和总体方差.
复习回顾
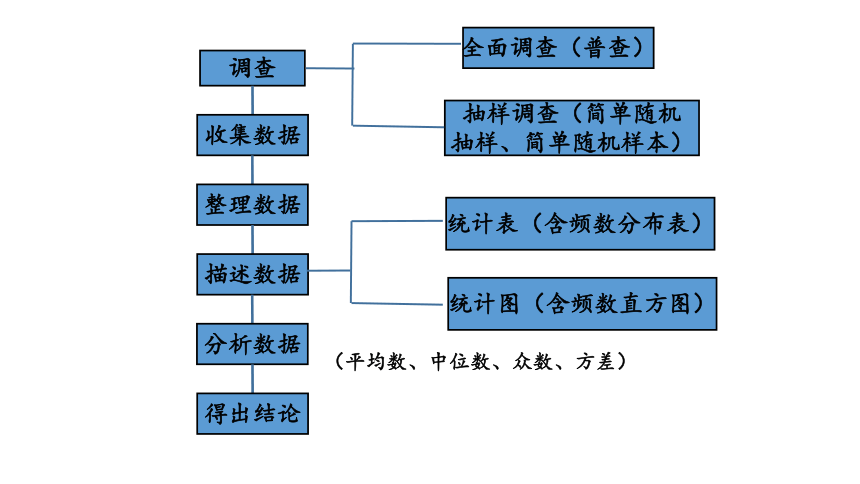
在前面几册学习中,我们认识了全面调查和抽样调查,并系统学习了收集、整理、描述和分析数据这样一个数据处理的基本过程 .
调查
收集数据
整理数据
描述数据
分析数据
得出结论
全面调查(普查)
抽样调查(简单随机抽样、简单随机样本)
统计表(含频数分布表)
统计图(含频数直方图)
(平均数、中位数、众数、方差)
我们在研究某个总体时,一般用数据表示总体中每个个体的某种数量特性,
所有这些数据组成一个总体,而样本则是从总体中抽取的部分数据,因此,
样本蕴含着总体的许多信息,这使得我们有可能通过样本的某些特性去推断
总体的相应特性.
从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,这是统计
的基本思想.用样本平均数、样本方差分别去估计总体平均数、总体方差就是
这一思想的一个体现.实践和理论都表明:对于简单随机样本,在大多数情况
下,当样本容量足够大时,这种估计是合理的.
新课导入
说一说
(1)如何估计某城市所有家庭一年内平均丢弃的塑料袋个数?
(2)在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度
比较整齐?
可以进行简单随机抽样,
然后用样本估计总体.
知识讲解
知识点1 用样本平均数、方差估计总体平均数、方差
由于简单随机样本客观地反映了实际情况,能够代表总体,因此我们可用简单随机样本的平均数和方差分别去估计总体的平均数与方差.例如,我们可以从某城市所有家庭中随机抽取一部分家庭,统计他们在一年内丢弃的塑料袋个数,然后求出它们的平均值,再用这个平均值去估计该城市所有家庭一年内平均丢弃的塑料袋个数.同样,我们可以从甲、乙两种棉花中各抽取一定量的棉花,分别统计它们的纤维长度的方差,再用这两个方差分别
去估计这两种棉花纤维长度的整齐性,方差小的棉花品种整齐性比较好.
动脑筋
某农科所在某地区选择了自然条件相同的两个试验区,用相同的管理技术
试种甲、乙两个品种的水稻各100亩.如何确定哪个品种的水稻在该地区更
有推广价值呢?
为了选择合适的稻种,我们需要关心这两种水稻的平均产量及产量的稳定性
(即方差).于是,待水稻成熟后,各自从这100亩水稻随机抽取10亩水稻,记
录它们的亩产量(样本),数据如下表所示:
种类 每亩水稻的产量/kg
甲 865 885 886 876 893 885 870 905 890 895
乙 870 875 884 885 886 888 882 890 895 896
可以求出,这10亩甲、乙品种的水稻的平均产量分别为:
由于这10亩水稻是简单随机抽取的,因此可以分别用这10亩水稻的平均产量去估计
这两种水稻大面积种植后的平均产量.
由于在试验区这两种水稻的平均产量相差很小,从而我们可以估计出大面积种植这
两种水稻后的平均产量也应相差很小,所以,单从平均产量这一角度来考虑,我们
还不能确定哪种水稻更有推广价值.因此,我们还需要考虑这两种水稻产量的稳定性.
利用计算器,我们可以计算出这10亩甲、乙品种水稻产量的方差分别为129.6,59.09.
由于59.09129.6,因此我们可以估计种植乙种水稻的产量要比种植甲种水稻的产量
稳定.从而我们可以得出:在该地区,种植乙种水稻更有推广价值.
典例精析
例1:某单位共有 280 位员工参加了社会公益捐款活动,从中任意抽取了 12 位员工的捐款数额,记录如下:
估计该单位的捐款总额.
捐款数额/元 30 50 80 100
员工人数 2 5 3 2
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
做一做
10
15
20
18
答:估计这个新品种黄瓜平均每株约结 13 根黄瓜.
解:
(根).
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
10
15
20
18
例2:老王家的鱼塘中放养了某种鱼 1500 条,若干年后,准备打捞出售.为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
(1)鱼塘中这种鱼平均每条重约多少千克?
鱼的条数 平均每条鱼的质量/千克
第1次 15 2.8
第2次 20 3.0
第3次 10 2.5
(2)若这种鱼放养的成活率是 82%,鱼塘中这种鱼约有多少千克?
(3)如果把这种鱼全部卖掉,价格为每千克 6.2 元,那么这种鱼的总收入是多少元?若投资成本为 14000 元,这种鱼的纯收入是多少元?
随 堂 小 测
1.某学校抽查了某班级某月10天的用电量, 结果(单位:千瓦时)如下表:
(1)这10天用电量的众数是 , 中位数是 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级, 该月共计30天, 试估计该校该月总的用电量.
13千瓦时
13千瓦时
用电量 8 9 10 13 14 15
天数 1 1 2 3 1 2
分析:(1)根据众数及中位数的定义即可求得;
(2)利用平均数的计算方法求解;
(3)将第(2)题的计算结果乘天数及班级数即得.
解:(1)13千瓦时 13千瓦时
(2)∵这个班级每天的平均用电量=8+9+10×2+13×3+14+15×2)=12(千瓦时),
∴这个班级平均每天的用电量为12千瓦时.
(3)∵12×20×30=7200(千瓦时),
∴估计该校该月总的用电量为7200千瓦时.
2.某鱼塘中养了某种鱼4000条, 为了估计该鱼塘中该种鱼的总质量, 从鱼塘中捕捞了3次,取得的数据如下:
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为12元, 求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数表达式, 并估计自变量x的取值范围.
数量/条 平均每条鱼的质量/kg
第1次捕捞 15 1.6
第2次捕捞 15 2.0
第3次捕捞 10 1.8
分析 :(1)根据平均数的计算公式求解;
(2)每条鱼的平均质量×总条数=总质量;
(3)根据题意列出函数表达式即可.
解 :(1)样本中平均每条鱼的质量为=1.8(kg).
(2)估计鱼塘中该种鱼的总质量为1.8×4000=7200(kg).
(3)出售该种鱼的收入y与出售该种鱼的质量x的函数表达式为y=12x,
估计自变量x的取值范围为0≤x≤7200.
解题归纳:根据“平均数= ”利用已知的两个量可求得第三个量, 如所有数据之和=平均数×数据总个数.
小结
利用样本方差估计总体方差
利用样本平均数估计总体平均数
总体平均数和方差的估计
第5章 用样本推断总体
5.1 总体平均数与方差的估计
学习目标
1.在理解样本与总体的关系的基础上,认识并体会统计估计的意义、实施方法及在实际问题中的应用.
2.知道可以通过样本平均数、样本方差推断总体平均数和总体方差.
复习回顾
在前面几册学习中,我们认识了全面调查和抽样调查,并系统学习了收集、整理、描述和分析数据这样一个数据处理的基本过程 .
调查
收集数据
整理数据
描述数据
分析数据
得出结论
全面调查(普查)
抽样调查(简单随机抽样、简单随机样本)
统计表(含频数分布表)
统计图(含频数直方图)
(平均数、中位数、众数、方差)
我们在研究某个总体时,一般用数据表示总体中每个个体的某种数量特性,
所有这些数据组成一个总体,而样本则是从总体中抽取的部分数据,因此,
样本蕴含着总体的许多信息,这使得我们有可能通过样本的某些特性去推断
总体的相应特性.
从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,这是统计
的基本思想.用样本平均数、样本方差分别去估计总体平均数、总体方差就是
这一思想的一个体现.实践和理论都表明:对于简单随机样本,在大多数情况
下,当样本容量足够大时,这种估计是合理的.
新课导入
说一说
(1)如何估计某城市所有家庭一年内平均丢弃的塑料袋个数?
(2)在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度
比较整齐?
可以进行简单随机抽样,
然后用样本估计总体.
知识讲解
知识点1 用样本平均数、方差估计总体平均数、方差
由于简单随机样本客观地反映了实际情况,能够代表总体,因此我们可用简单随机样本的平均数和方差分别去估计总体的平均数与方差.例如,我们可以从某城市所有家庭中随机抽取一部分家庭,统计他们在一年内丢弃的塑料袋个数,然后求出它们的平均值,再用这个平均值去估计该城市所有家庭一年内平均丢弃的塑料袋个数.同样,我们可以从甲、乙两种棉花中各抽取一定量的棉花,分别统计它们的纤维长度的方差,再用这两个方差分别
去估计这两种棉花纤维长度的整齐性,方差小的棉花品种整齐性比较好.
动脑筋
某农科所在某地区选择了自然条件相同的两个试验区,用相同的管理技术
试种甲、乙两个品种的水稻各100亩.如何确定哪个品种的水稻在该地区更
有推广价值呢?
为了选择合适的稻种,我们需要关心这两种水稻的平均产量及产量的稳定性
(即方差).于是,待水稻成熟后,各自从这100亩水稻随机抽取10亩水稻,记
录它们的亩产量(样本),数据如下表所示:
种类 每亩水稻的产量/kg
甲 865 885 886 876 893 885 870 905 890 895
乙 870 875 884 885 886 888 882 890 895 896
可以求出,这10亩甲、乙品种的水稻的平均产量分别为:
由于这10亩水稻是简单随机抽取的,因此可以分别用这10亩水稻的平均产量去估计
这两种水稻大面积种植后的平均产量.
由于在试验区这两种水稻的平均产量相差很小,从而我们可以估计出大面积种植这
两种水稻后的平均产量也应相差很小,所以,单从平均产量这一角度来考虑,我们
还不能确定哪种水稻更有推广价值.因此,我们还需要考虑这两种水稻产量的稳定性.
利用计算器,我们可以计算出这10亩甲、乙品种水稻产量的方差分别为129.6,59.09.
由于59.09129.6,因此我们可以估计种植乙种水稻的产量要比种植甲种水稻的产量
稳定.从而我们可以得出:在该地区,种植乙种水稻更有推广价值.
典例精析
例1:某单位共有 280 位员工参加了社会公益捐款活动,从中任意抽取了 12 位员工的捐款数额,记录如下:
估计该单位的捐款总额.
捐款数额/元 30 50 80 100
员工人数 2 5 3 2
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
做一做
10
15
20
18
答:估计这个新品种黄瓜平均每株约结 13 根黄瓜.
解:
(根).
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
10
15
20
18
例2:老王家的鱼塘中放养了某种鱼 1500 条,若干年后,准备打捞出售.为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
(1)鱼塘中这种鱼平均每条重约多少千克?
鱼的条数 平均每条鱼的质量/千克
第1次 15 2.8
第2次 20 3.0
第3次 10 2.5
(2)若这种鱼放养的成活率是 82%,鱼塘中这种鱼约有多少千克?
(3)如果把这种鱼全部卖掉,价格为每千克 6.2 元,那么这种鱼的总收入是多少元?若投资成本为 14000 元,这种鱼的纯收入是多少元?
随 堂 小 测
1.某学校抽查了某班级某月10天的用电量, 结果(单位:千瓦时)如下表:
(1)这10天用电量的众数是 , 中位数是 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级, 该月共计30天, 试估计该校该月总的用电量.
13千瓦时
13千瓦时
用电量 8 9 10 13 14 15
天数 1 1 2 3 1 2
分析:(1)根据众数及中位数的定义即可求得;
(2)利用平均数的计算方法求解;
(3)将第(2)题的计算结果乘天数及班级数即得.
解:(1)13千瓦时 13千瓦时
(2)∵这个班级每天的平均用电量=8+9+10×2+13×3+14+15×2)=12(千瓦时),
∴这个班级平均每天的用电量为12千瓦时.
(3)∵12×20×30=7200(千瓦时),
∴估计该校该月总的用电量为7200千瓦时.
2.某鱼塘中养了某种鱼4000条, 为了估计该鱼塘中该种鱼的总质量, 从鱼塘中捕捞了3次,取得的数据如下:
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为12元, 求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数表达式, 并估计自变量x的取值范围.
数量/条 平均每条鱼的质量/kg
第1次捕捞 15 1.6
第2次捕捞 15 2.0
第3次捕捞 10 1.8
分析 :(1)根据平均数的计算公式求解;
(2)每条鱼的平均质量×总条数=总质量;
(3)根据题意列出函数表达式即可.
解 :(1)样本中平均每条鱼的质量为=1.8(kg).
(2)估计鱼塘中该种鱼的总质量为1.8×4000=7200(kg).
(3)出售该种鱼的收入y与出售该种鱼的质量x的函数表达式为y=12x,
估计自变量x的取值范围为0≤x≤7200.
解题归纳:根据“平均数= ”利用已知的两个量可求得第三个量, 如所有数据之和=平均数×数据总个数.
小结
利用样本方差估计总体方差
利用样本平均数估计总体平均数
总体平均数和方差的估计
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
