4.4 第1课时 仰角、俯角问题 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册
文档属性
| 名称 | 4.4 第1课时 仰角、俯角问题 课件(共18张PPT) 2023-2024学年数学湘教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第4章 锐角三角函数
4.4 解直角三角形的应用
第1课时 仰角、俯角问题
学习目标
1.灵活运用直角三角形的各种关系,解决一些简单的实际问题,使学生进一步感受模型思想,感受数学的价值.
2.了解测量中的概念,并能灵活运用相关知识解决某些实际问题.
新课导入
在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.
对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
某探险者某天到达如
图所示的点 A 处时,他准
备估算出离他的目的地—
海拔 3 500 m 的山峰顶点
B 处的水平距离. 你能帮他
想出一个可行的办法吗?
.
A
B
.
.
动脑筋
知识讲解
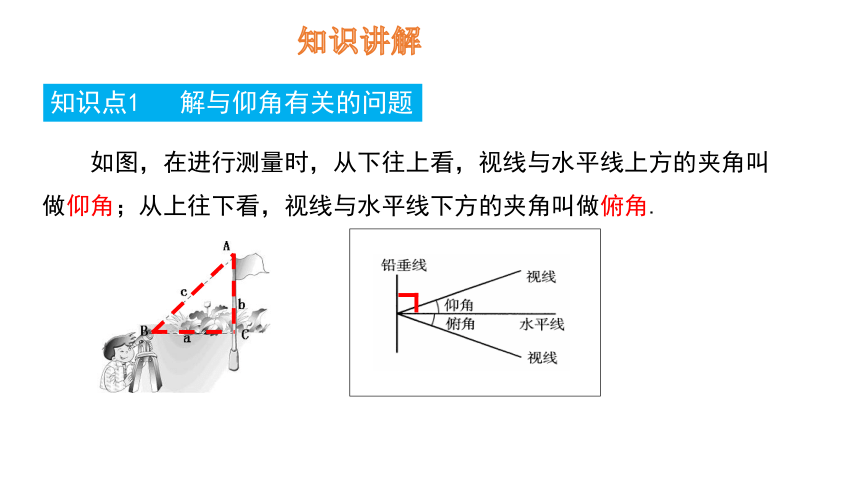
知识点1 解与仰角有关的问题
如图,在进行测量时,从下往上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
典例精析
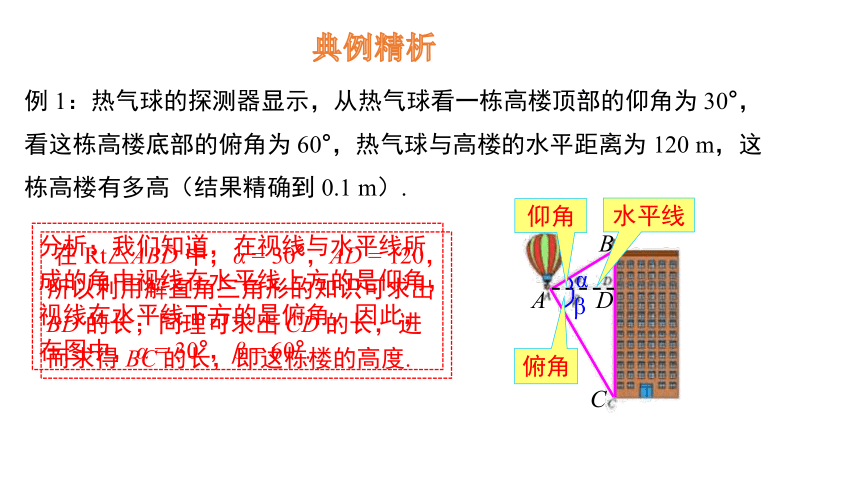
例 1:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 30°,看这栋高楼底部的俯角为 60°,热气球与高楼的水平距离为 120 m,这栋高楼有多高(结果精确到 0.1 m).
A
B
C
D
α
β
仰角
水平线
俯角
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α = 30°,β = 60°.
在 Rt△ABD 中,α = 30°,AD = 120,所以利用解直角三角形的知识可求出 BD 的长;同理可求出 CD 的长,进而求得 BC 的长,即这栋楼的高度.
解:如图,α = 30°,β = 60°, AD = 120.
答:这栋楼高约为 277.1 m.
A
B
C
D
α
β
解:如图,在Rt△ABC 中,∠BAC = 25°,AC = 1000 m,
因此 tan 25°==.
从而 BC = 1000×tan 25° ≈ 466.3(m),
BD = 466.3 + 1.7 = 468 ( m ).
答:上海东方明珠塔的高度 BD为 468 m.
例2:如图,在离上海东方明珠塔底部 1000 m 的 A 处,用仪器测得塔顶的仰角∠BAC为 25°,仪器距地面高 AE 为1.7 m.求上海东方明珠塔的高度 BD (结果精确到 1 m).
B
C
A
D
25°
E
例3:如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高是1.5 m. 那么该塔有多高 (结果精确到 1 m),你能帮小明算出该塔有多
高吗
D′
A
B′
B
D
C′
C
分析:由图可知,塔高 AB 可以分为上下两部分,上部分 AB′ 可以在 Rt△AD′B′ 和 Rt△AC′B′ 中利用仰角的正切值求出,B′B 与 D′D 相等.
解:如图,设 AB′ = x m.
由题意知∠AD′B′ = 30°,∠AC′B′ = 60°, D′C′ = 50 m.
∴∠D′AB′ = 60°,∠C′AB′ = 30°,D′C′ = 50 m .
D′
A
B′
B
D
C′
C
知识点2 解与俯角有关的问题
45°
30°
O
B
A
200 米
例4. 如图,直升飞机悬停在高为 200 米的大楼 AB 上方 P 点处,从大楼的顶部和底部测得飞机的仰角为 30° 和45°,求飞机的高度 PO.
P
解:如图,过点 P 作 PC⊥BA 交 BA 的延长线于点 C.则∠PBO =∠CPB = 45°,∠CPA = 30°.∴ PC = BC = 200 + AC,tan30° ==.
∴ AC = (100+100)米.
∴ PO = BC =(300+100)米.
C
1. 如图,在高出海平面 100 米的悬崖顶A 处,观测海平面上一艘小船 B,并测得它的俯角为 45°,则船与观测者之间的水平距离 BC =_____米.
B
C
A
100
随 堂 小 测
2. 如图,两建筑物AB 和CD 的水平距离为30米,从A点测得D点的俯角为30°,测得C 点的俯角为60°,则建筑物CD 的高为_____米.
B
C
A
D
30°
60°
3.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16°31′,求飞机A到控制点B距离(精确到1米).
分析:利用正弦可求.
答:飞机A到控制点B的距离约为4221米.
解:在Rt△ABC中,sin B=,∴AB===4221(米).
解:由题意,AC=AB=610(米).
4. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB 为610 米,远处有一栋大楼,某人在楼底C 处测得塔顶B的仰角为45°,在楼顶D 处测得塔顶B 的仰角为 39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
(2) 求大楼的高度 CD(精确到 1 米).
解:DE=AC=610(米),
在 Rt△BDE 中,tan∠BDE=.
故 BE=DE · tan39°.
∴ CD=AE=AB-BE=AB - DE · tan39°
=610-610×tan39° ≈ 116(米).
小结
利用仰、俯角解直角三角形
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
第4章 锐角三角函数
4.4 解直角三角形的应用
第1课时 仰角、俯角问题
学习目标
1.灵活运用直角三角形的各种关系,解决一些简单的实际问题,使学生进一步感受模型思想,感受数学的价值.
2.了解测量中的概念,并能灵活运用相关知识解决某些实际问题.
新课导入
在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.
对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
某探险者某天到达如
图所示的点 A 处时,他准
备估算出离他的目的地—
海拔 3 500 m 的山峰顶点
B 处的水平距离. 你能帮他
想出一个可行的办法吗?
.
A
B
.
.
动脑筋
知识讲解
知识点1 解与仰角有关的问题
如图,在进行测量时,从下往上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
典例精析
例 1:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 30°,看这栋高楼底部的俯角为 60°,热气球与高楼的水平距离为 120 m,这栋高楼有多高(结果精确到 0.1 m).
A
B
C
D
α
β
仰角
水平线
俯角
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α = 30°,β = 60°.
在 Rt△ABD 中,α = 30°,AD = 120,所以利用解直角三角形的知识可求出 BD 的长;同理可求出 CD 的长,进而求得 BC 的长,即这栋楼的高度.
解:如图,α = 30°,β = 60°, AD = 120.
答:这栋楼高约为 277.1 m.
A
B
C
D
α
β
解:如图,在Rt△ABC 中,∠BAC = 25°,AC = 1000 m,
因此 tan 25°==.
从而 BC = 1000×tan 25° ≈ 466.3(m),
BD = 466.3 + 1.7 = 468 ( m ).
答:上海东方明珠塔的高度 BD为 468 m.
例2:如图,在离上海东方明珠塔底部 1000 m 的 A 处,用仪器测得塔顶的仰角∠BAC为 25°,仪器距地面高 AE 为1.7 m.求上海东方明珠塔的高度 BD (结果精确到 1 m).
B
C
A
D
25°
E
例3:如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高是1.5 m. 那么该塔有多高 (结果精确到 1 m),你能帮小明算出该塔有多
高吗
D′
A
B′
B
D
C′
C
分析:由图可知,塔高 AB 可以分为上下两部分,上部分 AB′ 可以在 Rt△AD′B′ 和 Rt△AC′B′ 中利用仰角的正切值求出,B′B 与 D′D 相等.
解:如图,设 AB′ = x m.
由题意知∠AD′B′ = 30°,∠AC′B′ = 60°, D′C′ = 50 m.
∴∠D′AB′ = 60°,∠C′AB′ = 30°,D′C′ = 50 m .
D′
A
B′
B
D
C′
C
知识点2 解与俯角有关的问题
45°
30°
O
B
A
200 米
例4. 如图,直升飞机悬停在高为 200 米的大楼 AB 上方 P 点处,从大楼的顶部和底部测得飞机的仰角为 30° 和45°,求飞机的高度 PO.
P
解:如图,过点 P 作 PC⊥BA 交 BA 的延长线于点 C.则∠PBO =∠CPB = 45°,∠CPA = 30°.∴ PC = BC = 200 + AC,tan30° ==.
∴ AC = (100+100)米.
∴ PO = BC =(300+100)米.
C
1. 如图,在高出海平面 100 米的悬崖顶A 处,观测海平面上一艘小船 B,并测得它的俯角为 45°,则船与观测者之间的水平距离 BC =_____米.
B
C
A
100
随 堂 小 测
2. 如图,两建筑物AB 和CD 的水平距离为30米,从A点测得D点的俯角为30°,测得C 点的俯角为60°,则建筑物CD 的高为_____米.
B
C
A
D
30°
60°
3.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16°31′,求飞机A到控制点B距离(精确到1米).
分析:利用正弦可求.
答:飞机A到控制点B的距离约为4221米.
解:在Rt△ABC中,sin B=,∴AB===4221(米).
解:由题意,AC=AB=610(米).
4. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB 为610 米,远处有一栋大楼,某人在楼底C 处测得塔顶B的仰角为45°,在楼顶D 处测得塔顶B 的仰角为 39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
(2) 求大楼的高度 CD(精确到 1 米).
解:DE=AC=610(米),
在 Rt△BDE 中,tan∠BDE=.
故 BE=DE · tan39°.
∴ CD=AE=AB-BE=AB - DE · tan39°
=610-610×tan39° ≈ 116(米).
小结
利用仰、俯角解直角三角形
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
