数学:3.1.1《函数的零点》课件(新人教a版必修1)
文档属性
| 名称 | 数学:3.1.1《函数的零点》课件(新人教a版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 303.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览





文档简介
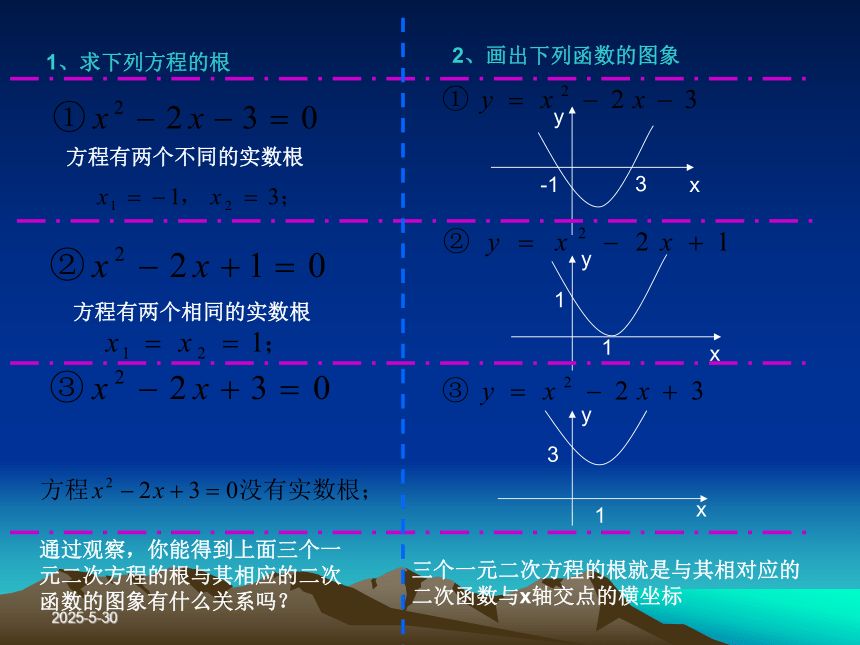
课件20张PPT。§3.1.1 函数的零点2019-3-13一、问题情境:(1)y=x2-2x-3 与 x2-2x-3=0(2)y=x2-2x+1 与 x2-2x+1=0(3)y=x2-2x+3 与 x2-2x+3=0引申:二次函数y=ax2+bx+c (a≠0)的图象和相应一元二次方程ax2+bx+c=0(a≠0)的根有何关系?结论: 二次函数图象与x轴交点的横坐标
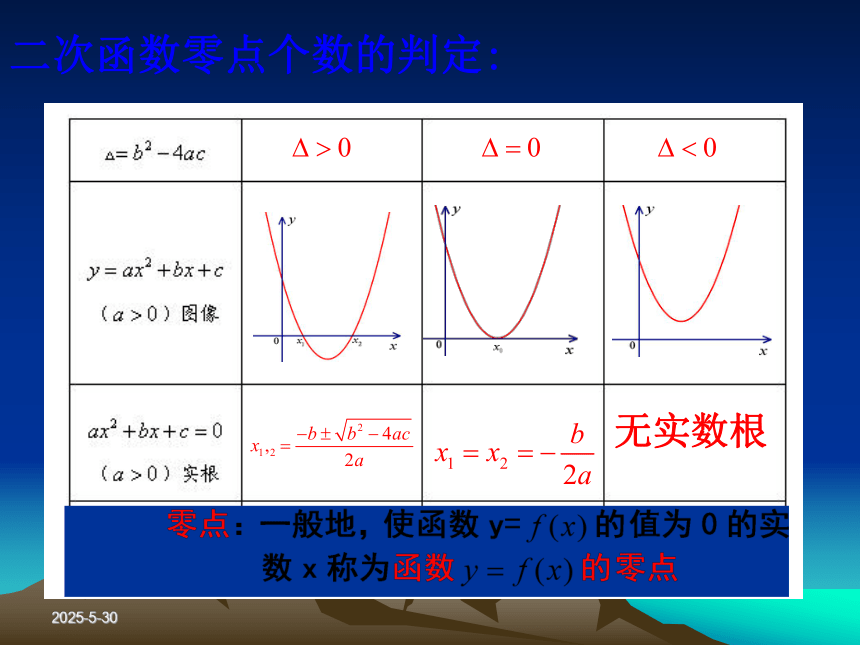
就是相应方程的实数根。问题1:下列二次函数的图象和相应二次方程的根有何关系?2019-3-13通过观察,你能得到上面三个一元二次方程的根与其相应的二次函数的图象有什么关系吗?三个一元二次方程的根就是与其相对应的二次函数与x轴交点的横坐标2019-3-13无实数根零点无零点二次函数零点个数的判定:2019-3-13二、讲授新知1、函数零点的概念:2、函数零点的意义:2019-3-13 所以:例1:求下列函数的零点:2019-3-13(代数法)(几何法) 例2.已知函数y=x2-2x-1
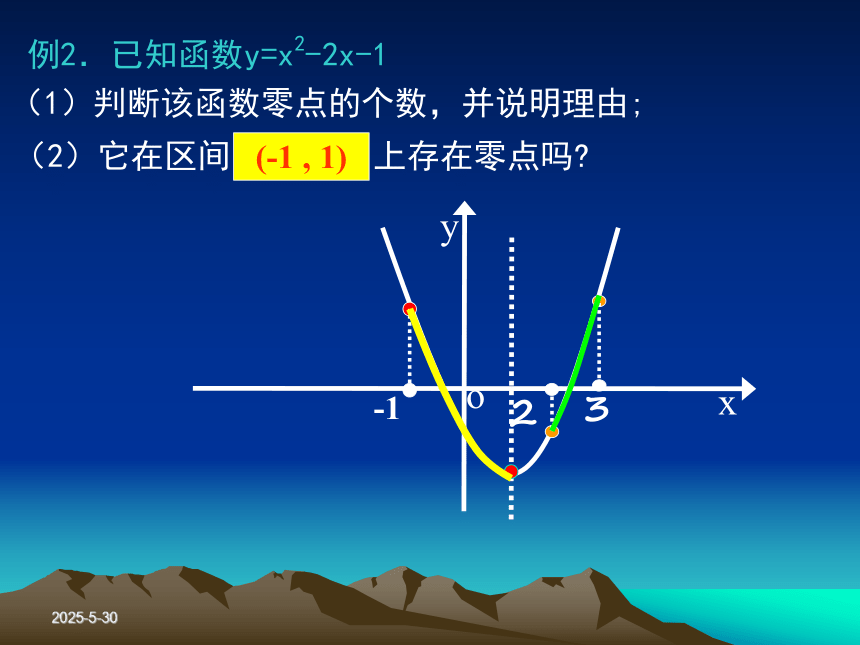
(1)判断该函数零点的个数,并说明理由;2019-3-13 例2.已知函数y=x2-2x-1
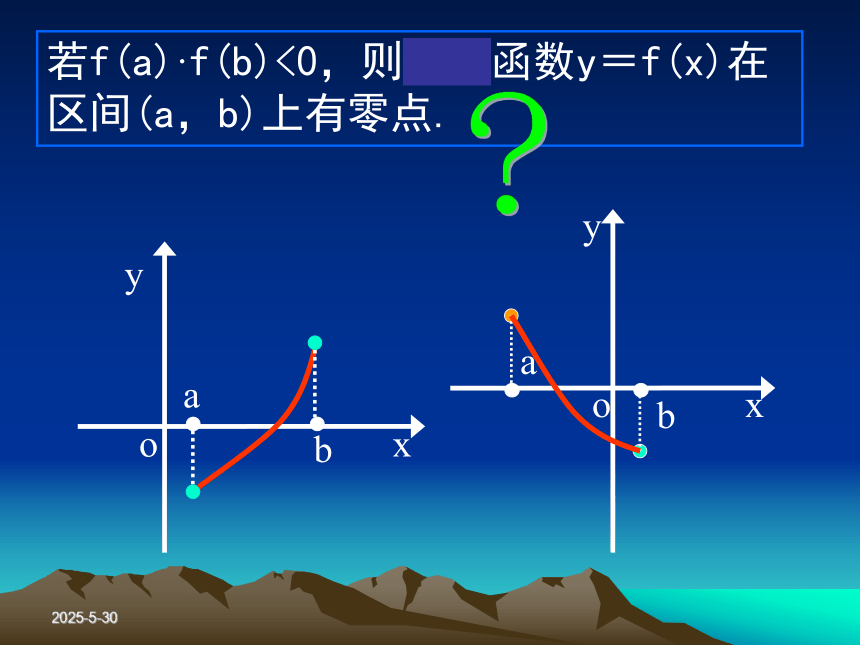
(1)判断该函数零点的个数,并说明理由;(2)它在区间( 2 , 3)上存在零点吗?(-1 , 1)2019-3-13若f(a)·f(b)<0,则二次函数y=f(x)在区间(a,b)上有零点.?2019-3-13若f(a)·f(b)<0,则二次函数y=f(x)在区间(a,b)上有零点.若函数y=f(x)在区间 (a,b)上的图象是一条不间断的曲线,且f(a) ·f(b)<0,则函数y=f(x)在区间(a,b)上有零点.2019-3-132019-3-13 例3:试证明函数f(x)=x3+x2+1在区间(-2,-1)上有零点.证明:∵ f(-2)=-3<0, f(-1)=1>0又∵ 函数f(x)在区间( -2,-1 )上的图象是不间 断的,∴ 函数f(x)在区间(-2,-1)上存在零点.∴ f(-2) ·f(-1)<02019-3-13例4:已知函数
(1) 证明:函数有两个零点。
(2)若函数在区间 有零点,求a的取值范围。
2019-3-13法一2019-3-13法二由图可得两函数图象只有一个公共点,
所以函数有一个零点。2019-3-13242019-3-13三、练习应用有有无<>>2019-3-132019-3-13方程f(x)=0
的实数根函数y=f(x) 的图象与x轴交点的横坐标函数y=f(x)的零点数形四、小结:2019-3-13四、小结:2019-3-13
就是相应方程的实数根。问题1:下列二次函数的图象和相应二次方程的根有何关系?2019-3-13通过观察,你能得到上面三个一元二次方程的根与其相应的二次函数的图象有什么关系吗?三个一元二次方程的根就是与其相对应的二次函数与x轴交点的横坐标2019-3-13无实数根零点无零点二次函数零点个数的判定:2019-3-13二、讲授新知1、函数零点的概念:2、函数零点的意义:2019-3-13 所以:例1:求下列函数的零点:2019-3-13(代数法)(几何法) 例2.已知函数y=x2-2x-1
(1)判断该函数零点的个数,并说明理由;2019-3-13 例2.已知函数y=x2-2x-1
(1)判断该函数零点的个数,并说明理由;(2)它在区间( 2 , 3)上存在零点吗?(-1 , 1)2019-3-13若f(a)·f(b)<0,则二次函数y=f(x)在区间(a,b)上有零点.?2019-3-13若f(a)·f(b)<0,则二次函数y=f(x)在区间(a,b)上有零点.若函数y=f(x)在区间 (a,b)上的图象是一条不间断的曲线,且f(a) ·f(b)<0,则函数y=f(x)在区间(a,b)上有零点.2019-3-132019-3-13 例3:试证明函数f(x)=x3+x2+1在区间(-2,-1)上有零点.证明:∵ f(-2)=-3<0, f(-1)=1>0又∵ 函数f(x)在区间( -2,-1 )上的图象是不间 断的,∴ 函数f(x)在区间(-2,-1)上存在零点.∴ f(-2) ·f(-1)<02019-3-13例4:已知函数
(1) 证明:函数有两个零点。
(2)若函数在区间 有零点,求a的取值范围。
2019-3-13法一2019-3-13法二由图可得两函数图象只有一个公共点,
所以函数有一个零点。2019-3-13242019-3-13三、练习应用有有无<>>2019-3-132019-3-13方程f(x)=0
的实数根函数y=f(x) 的图象与x轴交点的横坐标函数y=f(x)的零点数形四、小结:2019-3-13四、小结:2019-3-13
