数学:3.2.1《几类不同增长的函数模型》课件(新人教a版必修1)
文档属性
| 名称 | 数学:3.2.1《几类不同增长的函数模型》课件(新人教a版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 104.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:06:00 | ||
图片预览




文档简介
课件16张PPT。2019/3/133.2.1几类不同增长的函数模型2019/3/13新课导入 一张纸的厚度大约为0.01cm,一块砖的厚度
大约为10cm,请同学们计算将一张纸对折x次的厚
度和x块砖的厚度各是多少,列出函数关系式,并
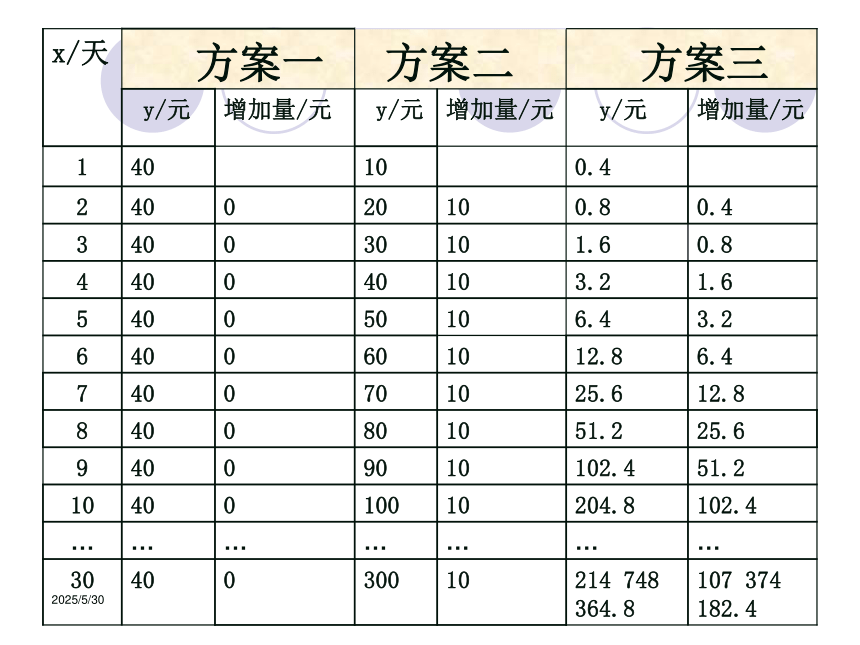
计算n=20时它们的厚度,你的直觉与结果一致吗?解:设一张纸对折x次的厚度为f(x),x块砖的厚度为g(x),依题意可得:2019/3/13应用示例例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?2019/3/13
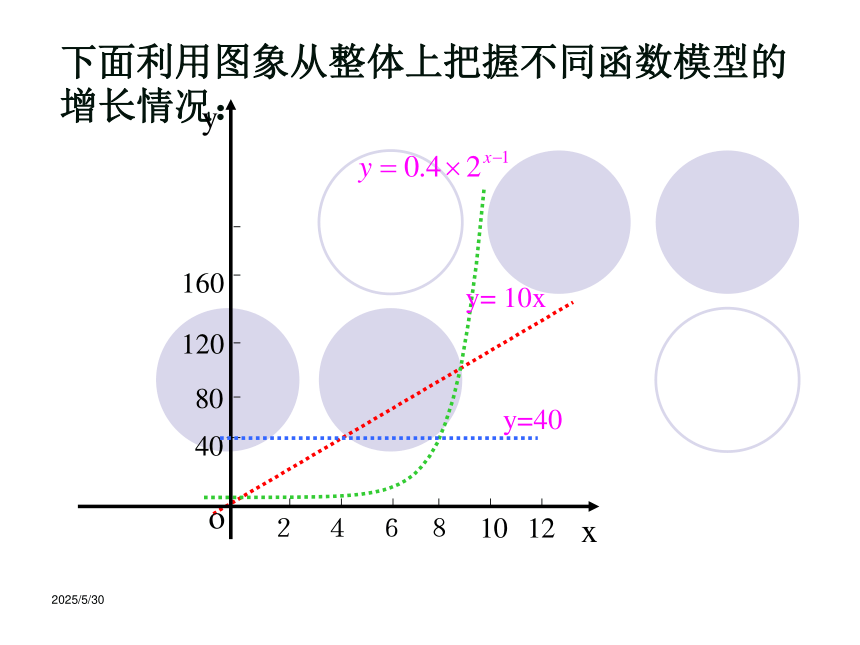
三个模型中,第一个是常数函数,后两个都是递增模型,要对三个方案作出选择,就要对他们的增长情况进行分析,首先计算得到三种方案所得回报的增长情况如下表所示:方案一可以用函数 进行描述;方案二可以用函数 进行描述;方案三可以用函数 进行描述
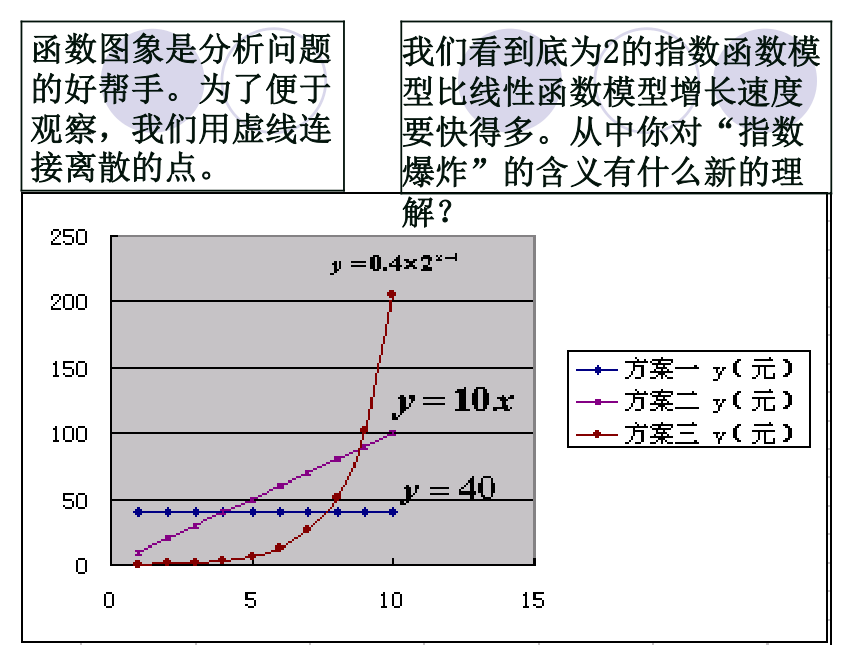
解:设第x天所得回报是y元,由题意得:2019/3/132019/3/13下面利用图象从整体上把握不同函数模型的增长情况:yxoy=40y= 10x2019/3/13我们看到底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?2019/3/13结合表格及三个函数的图像从每天的回报看:
第1--4天,方案一回报最多: 第5--8天,方案二回报最多:
第9天以后,方案三回报最多。 思考:能否根据上面的分析作出这样的选择:
投资5天以下选择方案一;
投资5--8天选择方案二;
投资8天以上选择方案三?
2019/3/13x(天)方案一 方案二 方案三
回报(元) 回报(元) 回报(元)
1 40 10 0.4
2 80 30 1.2
3 120 60 2.8
4 160 100 6
5 200 150 12.4
6 240 210 25.2
7 280 280 50.8
8 320 360 102
9 360 450 204.4
10 400 550 409.2
11 440 660 818.8
12 480 780 1638 结论
投资1~6天,应选择第一种投资方案;投资7天,应选择方案一或者方案二;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。累计的回报数:2019/3/13例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的方案 :在销售利润达到10万元时,按销售利润进行奖励且奖金y(单位:万元)随销售利润 x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,现有三个奖励模型:
, , ,
其中哪个模型能符合公司的要求?2019/3/13(1)奖金总数不超过5万元(2)奖金不超过利润的25%分析:选择的模型需要满足的要求如下:2019/3/13Xyoy=5y=0.25x2019/3/13首先计算哪个模型的奖金总数不超过5万对于模型 ,在区间[10,1000]上递增,令0.25x=5,
可得x=20,因此当x>20时,y>5,所以该模型不符合要求;对于模型 ,由函数图像,它在区间[10,1000]上递增,而且当x=1000 时 所以它符合奖金总数不超过5万的要求。对于模型 ,根据图像令y=5,利用计算器可知在区间(805,806)内有一个点 满足 ,它在区间[10,1000]上递增, 故当 时,y>5,所以该模型也不符合要求。2019/3/13对于函数模型 当 时,奖金是否不超过利润的25%呢?利用计算机作出图像,有图像可知它是递减的,
因此有答:模型 能符合公司的要求2019/3/13(1)读题理解题意
(2)挖掘数量关系,建立数学模型
(3)求解数学问题
(4)回归实际,进行答题2、求解数学应用问题的一般步骤:小结1、几种不同增长的函数体会直线上升,指数爆炸,对数增长等不同类型函数的含义与差异性
利用数据表格,函数图像确定函数模型2019/3/13课后作业1.课本P107习题3.2A组1、2
2.举出生活实例,并用函数模型进行分析。
大约为10cm,请同学们计算将一张纸对折x次的厚
度和x块砖的厚度各是多少,列出函数关系式,并
计算n=20时它们的厚度,你的直觉与结果一致吗?解:设一张纸对折x次的厚度为f(x),x块砖的厚度为g(x),依题意可得:2019/3/13应用示例例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?2019/3/13
三个模型中,第一个是常数函数,后两个都是递增模型,要对三个方案作出选择,就要对他们的增长情况进行分析,首先计算得到三种方案所得回报的增长情况如下表所示:方案一可以用函数 进行描述;方案二可以用函数 进行描述;方案三可以用函数 进行描述
解:设第x天所得回报是y元,由题意得:2019/3/132019/3/13下面利用图象从整体上把握不同函数模型的增长情况:yxoy=40y= 10x2019/3/13我们看到底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?2019/3/13结合表格及三个函数的图像从每天的回报看:
第1--4天,方案一回报最多: 第5--8天,方案二回报最多:
第9天以后,方案三回报最多。 思考:能否根据上面的分析作出这样的选择:
投资5天以下选择方案一;
投资5--8天选择方案二;
投资8天以上选择方案三?
2019/3/13x(天)方案一 方案二 方案三
回报(元) 回报(元) 回报(元)
1 40 10 0.4
2 80 30 1.2
3 120 60 2.8
4 160 100 6
5 200 150 12.4
6 240 210 25.2
7 280 280 50.8
8 320 360 102
9 360 450 204.4
10 400 550 409.2
11 440 660 818.8
12 480 780 1638 结论
投资1~6天,应选择第一种投资方案;投资7天,应选择方案一或者方案二;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。累计的回报数:2019/3/13例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的方案 :在销售利润达到10万元时,按销售利润进行奖励且奖金y(单位:万元)随销售利润 x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,现有三个奖励模型:
, , ,
其中哪个模型能符合公司的要求?2019/3/13(1)奖金总数不超过5万元(2)奖金不超过利润的25%分析:选择的模型需要满足的要求如下:2019/3/13Xyoy=5y=0.25x2019/3/13首先计算哪个模型的奖金总数不超过5万对于模型 ,在区间[10,1000]上递增,令0.25x=5,
可得x=20,因此当x>20时,y>5,所以该模型不符合要求;对于模型 ,由函数图像,它在区间[10,1000]上递增,而且当x=1000 时 所以它符合奖金总数不超过5万的要求。对于模型 ,根据图像令y=5,利用计算器可知在区间(805,806)内有一个点 满足 ,它在区间[10,1000]上递增, 故当 时,y>5,所以该模型也不符合要求。2019/3/13对于函数模型 当 时,奖金是否不超过利润的25%呢?利用计算机作出图像,有图像可知它是递减的,
因此有答:模型 能符合公司的要求2019/3/13(1)读题理解题意
(2)挖掘数量关系,建立数学模型
(3)求解数学问题
(4)回归实际,进行答题2、求解数学应用问题的一般步骤:小结1、几种不同增长的函数体会直线上升,指数爆炸,对数增长等不同类型函数的含义与差异性
利用数据表格,函数图像确定函数模型2019/3/13课后作业1.课本P107习题3.2A组1、2
2.举出生活实例,并用函数模型进行分析。
