沪教版九年级数学下册试题 期末模拟测试卷(基础过关)(含解析)
文档属性
| 名称 | 沪教版九年级数学下册试题 期末模拟测试卷(基础过关)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 336.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 16:11:11 | ||
图片预览



文档简介
期末测试卷(基础过关)
一、选择题(每小题4分,共24分)
1.已知△ABC的外接圆⊙O,那么点O是△ABC的( )
A.三条中线交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线交点
2.如图,BC是⊙O的直径,点A是⊙O上的一点,∠C=31°,则∠B的度数是( )
A.59° B.60° C.62° D.69°
3.某中学为检查七年级学生的视力情况,对七年级全体300名学生进行了体检,并制作了如图所示的扇形统计图,由该图可以看出七年级学生视力不良的有( )
A.45名 B.120名 C.135名 D.165名
4.如图,四边形ABCD的顶点A,B,C在圆上,且边CD与该圆交于点E,AC,BE交于点F.下列角中,弧AE所对的圆周角是( )
A.∠ADE B.∠AFE C.∠ABE D.∠ABC
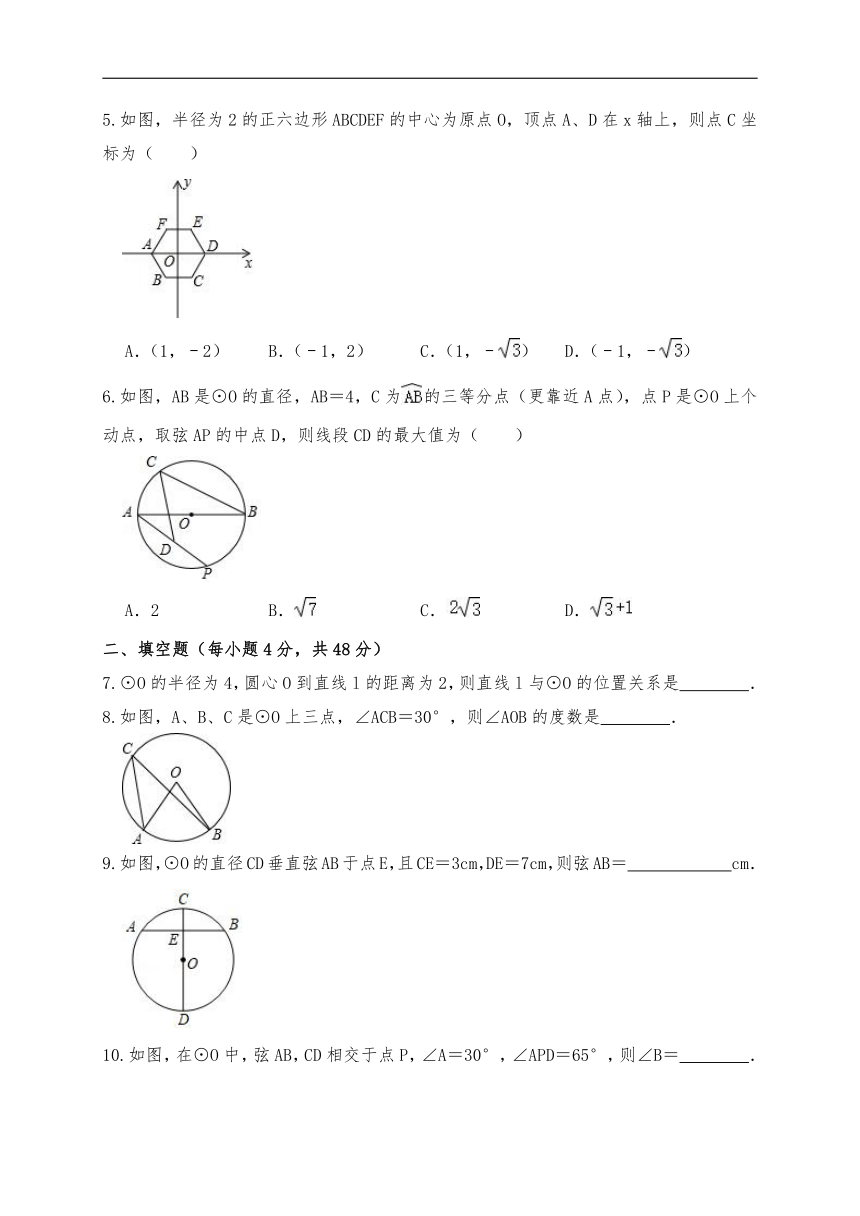
5.如图,半径为2的正六边形ABCDEF的中心为原点O,顶点A、D在x轴上,则点C坐标为( )
A.(1,﹣2) B.(﹣1,2) C.(1,﹣) D.(﹣1,﹣)
6.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
二、填空题(每小题4分,共48分)
7.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是 .
8.如图,A、B、C是⊙O上三点,∠ACB=30°,则∠AOB的度数是 .
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
10.如图,在⊙O中,弦AB,CD相交于点P,∠A=30°,∠APD=65°,则∠B= .
11.如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是 .
12.如图,在⊙O中,直径AB=4,弦CD⊥AB于E,若∠A=30°,则CD= .
13.为了了解某区七年级学生的视力情况,随机抽取了该区500名七年级学生进行调查.整理样本数据,得到下表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区12000名七年级学生视力低于4.8的约有 .
14.如图,一块含30°的直角三角板ABC(∠BAC=30°)的斜边AB与角器的直径重合,与点D对应的刻度读数是54°,则∠BCD的度数为 度.
15.如图,AB,CD是⊙O的直径,且AB⊥CD,P为CD延长线上的一点,PE切⊙O于E.BE交CD于F.若AB=6,DP=2,则BF= .
16.如图,已知PA,PB是⊙O的两条切线,A,B为切点.C是⊙O上一个动点,且不与A,B重合.若∠PAC=α,∠ABC=β,则α与β的关系是 .
17.如图是我国年财政收人同比(与上一年比较)增长率的折线统计图,其中2017年我国财政收入约为25000亿元.下列说法:
①2016年我国财政收入约为250000(1﹣195%)亿元;
②这四年中,2018年我国财政收人最少;
③2019年我国财政收入约为250000(1+11.7%)(1+21.3%)亿元.
其中正确的有 .(只需填出序号)
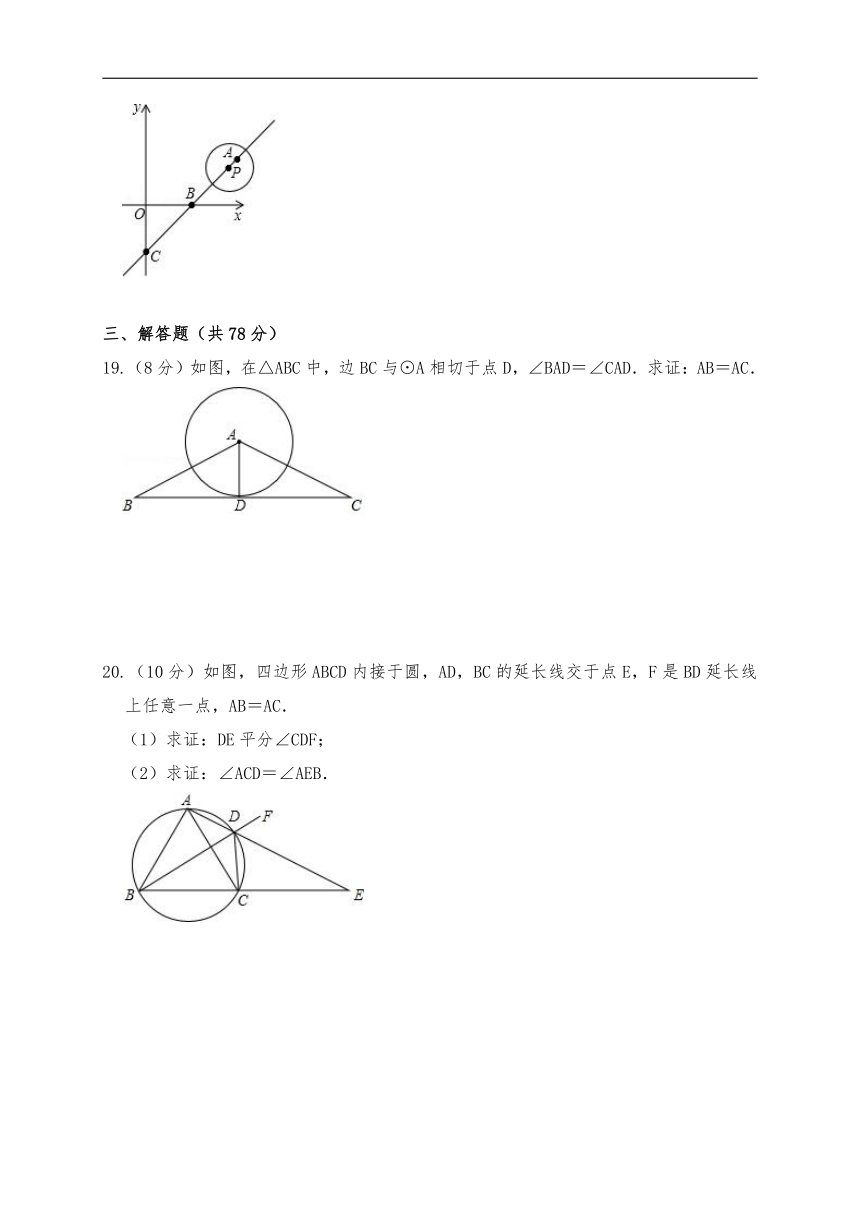
18.在平面直角坐标系中,直线y=x﹣2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m)出发以每秒个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t= 秒时,⊙P与坐标轴相切.
三、解答题(共78分)
19.(8分)如图,在△ABC中,边BC与⊙A相切于点D,∠BAD=∠CAD.求证:AB=AC.
20.(10分)如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
(1)求证:DE平分∠CDF;
(2)求证:∠ACD=∠AEB.
21.(12分)如图,Rt△ACB中,以BC边上一点O为圆心作圆,⊙O与边AC、AB分别切于点C、D,⊙O与BC另一交点为E.
(1)求证:BD AB=OB BC;
(2)若⊙O的半径为5,AC=,求BD的长.
22.(12分)期末,学校为了调查这学期学生课外阅读情况,随机抽样调查了一部分学生阅读课外书的本数,并将收集到的数据整理成如图的统计图.
(1)这次一共调查的学生人数是 人;
(2)所调查学生读书本数的众数是 本,中位数是 本.
(3)若该校有800名学生,请你估计该校学生这学期读书总数是多少本?
23.(12分)为了解居民对垃圾分类的知晓程度(“A.非常了解”“B.了解”“C.基本了解”“D.不太了解”),佳佳随机调查了若干人.根据调查结果绘制成如下两幅不完整的统计图:
(1)随机调查了 人,扇形统计图中表示“A”的扇形圆心角为 °
(2)补全条形统计图;
(3)估计在10000名市民中基本了解垃圾分类的人数.
24.(12分)如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.
25.(12分)如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=,求⊙O的半径.
答案
一、选择题
1.解:已知⊙O是△ABC的外接圆,那么点O一定是△ABC的三边的垂直平分线的交点,
故选:C.
2.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠B=90°﹣∠C=90°﹣31°=59°.
故选:A.
3.解:300×(40%+15%)=165人,
故选:D.
4.解:弧AE所对的圆周角为∠ABE和∠ACE.
故选:C.
5.解:连接OC.
∵∠COD==60°,OC=OD,
∴△COD是等边三角形,
∴OC=OD=2.
设BC交y轴于G,则∠GOC=30°.
在Rt△GOC中,∵∠GOC=30°,OC=2,
∴GC=1,OG=.
∴C(1,﹣).
故选:C.
6.解:如图,连接OD,OC,
∵AD=DP,
∴OD⊥PA,
∴∠ADO=90°,
∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,
当点D在CK的延长线上时,CD的值最大,
∵C为的三等分点,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴CK⊥OA,
在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,
∴CK==,
∵DK=OA=1,
∴CD=+1,
∴CD的最大值为+1,
故选:D.
二、填空题
7.解:∵圆心O到直线l的距离是2,小于⊙O的半径为4,
∴直线l与⊙O相交.
故答案为:相交.
8.解:∵A、B、C是⊙O上三点,∠ACB=30°,
∴∠AOB的度数是:2∠ACB=60°.
故答案为:60°.
9.解:连接OA,如图,
∵CE=3,DE=7,
∴CD=10,
∴OC=OA=5,OE=2,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==,
∴AB=2AE=2(cm).
故答案为2.
10.解:∵∠APD=∠C+∠A,
∴∠C=65°﹣30°=35°,
∴∠B=∠C=35°.
故答案为35°.
11.解:连结OB,如图,
∵AB与⊙O相切,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∵∠AOB=∠C+∠OBC,
而∠C=∠OBC,
∴∠C=AOB=30°.
故答案为:30°.
12.解:由圆周角定理得,∠COB=2∠A=60°,
∴CE=OC sin∠COE=2×=,
∵AE⊥CD,
∴CD=2CE=2,
故答案为:2,
13.解:估计该区12000名七年级学生视力低于4.8的约有12000×=4800(名),
故答案为:4800名.
14.解:∵∠C=90°,
∴点C在量角器所在的圆上
∵点D对应的刻度读数是54°,即∠AOD=54°,
∴∠ACD=∠AOD=27°,
∴∠BCD=90°﹣27°=63°.
故答案为63.
15.解:如图,连接OE,
∵∠PEF=90°﹣∠OEB=90°﹣∠OBE=∠OFB=∠EFP,
∴PF=PE,
∵AB=6,AB,CD是⊙O的直径,
∴OE=OD=OC=OB=OA=3,
∵PE切⊙O于E,
∴∠PEO=90°,
在Rt△OPE中,DP=2,
OP=3+2=5,
由勾股定理可得OP2=PE2+OE2,
∴52=PE2+32,解得PE=4,
∴PF=PE=4,OF=OP﹣PF=5﹣4=1,
∵AB⊥CD,
∴∠BOF=90°,
在Rt△OBF中,由勾定理可得BF2=OB2+OF2,
即BF2=32+12=10,
∴FB=.
故答案为:.
16.解:连接OA,OB,
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∵OA=OB,
∴∠OAB=∠OBA,
分两种情况:
①当C在优弧AB上时,如图1,
∵∠PAC=α,∠ABC=β,
∴α+β=∠PAC+∠ABC,
=90°+∠OAC+∠ABC,
=90°+∠OAC+180°﹣∠C﹣∠BAC,
=270°+∠OAC﹣AOB﹣∠OAB﹣∠OAC,
=270°﹣﹣∠OAB,
△OAB中,∠AOB+∠OAB+∠OBA=180°,
∴+∠OAB=90°,
∴α+β=270°﹣90°=180°;
②当C在劣弧AB上时,如图2,
∵∠PAO=∠PBO=90°,∠OAB=∠OBA,∠CBP=∠CAB,
∴∠PAC=∠ABC,
即α=β,
综上,α与β的关系是:α+β=180°或α=β;
故答案为:α+β=180°或α=β.
17.解:①2016年的财政收入应该是,故本选项错误;
②因为是正增长,所以2018年比2017年和2016年都高,故本选项错误;
③2019年我国财政收入约为25000(1+11.7%)(1+21.3%)亿元,故本选项正确;
其中正确的有③;
故答案为:③.
18.解:设⊙P与坐标轴的切点为D,
∵直线y=x﹣2与x轴、y轴分别交于点B、C,点A(4,m),
∴x=0时,y=﹣2,y=0时,x=2,x=4时,y=2,
∴A(4,2),B(2,0),C(0,﹣2),
∴AB=2,AC=2,OB=OC=2,
∴△OBC是等腰直角三角形,∠OBC=45°,
①当⊙P与x轴相切时,
∵点D是切点,⊙P的半径是1,
∴PD⊥x轴,PD=1,
∴△BDP是等腰直角三角形,
∴BD=PD=1,PB=,
∴AP=AB﹣PB=,
∵点P的速度为每秒个单位长度,
∴t=1;
②如图,⊙P与x轴和y轴都相切时,
∵PB=,
∴AP=AB+PB=3,
∵点P的速度为每秒个单位长度,
∴t=3;
③当点P只与y轴相切时,
∵PB=,
∴AP=AC+PB=5,
∵点P的速度为每秒个单位长度,
∴t=5.
综上所述,则当t=1或3或5秒时,⊙P与坐标轴相切,
故答案为:1或3或5.
三、解答题
19.解:∵BC与⊙A相切于点D,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(ASA),
∴AB=AC.
20.(1)证明:∵四边形ABCD内接于圆,
∴∠CDE=∠ABC,
由圆周角定理得,∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,
∴∠CAE+∠E=∠ABD+∠DBC,
又∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.
21.(1)证明:连接DO,如图所示.
∵,⊙O与边AC、AB分别切于点C、D,
∴∠ODB=90°=∠ACB.
又∵∠B=∠B,
∴△BDO∽△BCA,
∴=,
∴BD AB=OB BC.
(2)解:设BD=x,则BO==,BC=BO+OC=+5.
∵△BDO∽△BCA,
∴=,即=,
整理,得:7x2﹣120x=0,
解得:x1=,x2=0(舍去,不合题意),
经检验,x=是原方程的解,且符合题意,
∴BD的长为.
22.解:(1)1+1+3+4+6+2+2+1=20,
故答案为:20;
(2)众数是4
中位数是4,;
故答案为:4;4;
(3)每个人读书本数的平均数是:
=(1+2×1+3×3+4×6+5×4+6×2+7×2+8)
=4.5
∴总数是:800×4.5=3600
答:估计该校学生这学期读书总数约3600本.
23.解:(1)150÷30%=500人,360°×30%=108°,
故答案为:500,108;
(2)500×40%=200人,补全条形统计图如图所示:
(3)10000×=2000人,
答:在10000名市民中基本了解垃圾分类的人数为2000人.
24.(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC.
又AB=AC=13,BC=10,D是BC的中点,
∴BD=5.
连接OD;
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线;
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8
∴S阴影=S扇形AOE﹣S△AOE=4π﹣8.
25.(1)证明:连接OB,
∵BE为⊙O的切线,
∴OB⊥BE,
∴∠OBE=90°,
∴∠ABE+∠OBA=90°,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠ABE+∠OAB=90°,
∵AD是⊙O的直径,
∴∠OAB+∠ADB=90°,
∴∠ABE=∠ADB,
∵四边形ABCD的外接圆为⊙O,
∴∠EAB=∠C,
∵∠E=∠DBC,
∴∠ABE=∠BDC,
∴∠ADB=∠BDC,
即DB平分∠ADC;
(2)解:∵tan∠ABE=,
∴设AB=x,则BD=2x,
AD==x,
∵∠E=∠E,∠ABE=∠BDE,
∴△AEB∽△BED,
∴BE2=AE DE,且==,
设AE=a,则BE=2a,
∴4a2=a(a+x),
∴a=x,
∵∠BAE=∠C,∠ABE=∠BDC,
∴△AEB∽△CBD,
∴,
∴=,
解得=3,
∴AD=x=15,
∴OA=.
一、选择题(每小题4分,共24分)
1.已知△ABC的外接圆⊙O,那么点O是△ABC的( )
A.三条中线交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线交点
2.如图,BC是⊙O的直径,点A是⊙O上的一点,∠C=31°,则∠B的度数是( )
A.59° B.60° C.62° D.69°
3.某中学为检查七年级学生的视力情况,对七年级全体300名学生进行了体检,并制作了如图所示的扇形统计图,由该图可以看出七年级学生视力不良的有( )
A.45名 B.120名 C.135名 D.165名
4.如图,四边形ABCD的顶点A,B,C在圆上,且边CD与该圆交于点E,AC,BE交于点F.下列角中,弧AE所对的圆周角是( )
A.∠ADE B.∠AFE C.∠ABE D.∠ABC
5.如图,半径为2的正六边形ABCDEF的中心为原点O,顶点A、D在x轴上,则点C坐标为( )
A.(1,﹣2) B.(﹣1,2) C.(1,﹣) D.(﹣1,﹣)
6.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
二、填空题(每小题4分,共48分)
7.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是 .
8.如图,A、B、C是⊙O上三点,∠ACB=30°,则∠AOB的度数是 .
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
10.如图,在⊙O中,弦AB,CD相交于点P,∠A=30°,∠APD=65°,则∠B= .
11.如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是 .
12.如图,在⊙O中,直径AB=4,弦CD⊥AB于E,若∠A=30°,则CD= .
13.为了了解某区七年级学生的视力情况,随机抽取了该区500名七年级学生进行调查.整理样本数据,得到下表:
视力 4.7以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区12000名七年级学生视力低于4.8的约有 .
14.如图,一块含30°的直角三角板ABC(∠BAC=30°)的斜边AB与角器的直径重合,与点D对应的刻度读数是54°,则∠BCD的度数为 度.
15.如图,AB,CD是⊙O的直径,且AB⊥CD,P为CD延长线上的一点,PE切⊙O于E.BE交CD于F.若AB=6,DP=2,则BF= .
16.如图,已知PA,PB是⊙O的两条切线,A,B为切点.C是⊙O上一个动点,且不与A,B重合.若∠PAC=α,∠ABC=β,则α与β的关系是 .
17.如图是我国年财政收人同比(与上一年比较)增长率的折线统计图,其中2017年我国财政收入约为25000亿元.下列说法:
①2016年我国财政收入约为250000(1﹣195%)亿元;
②这四年中,2018年我国财政收人最少;
③2019年我国财政收入约为250000(1+11.7%)(1+21.3%)亿元.
其中正确的有 .(只需填出序号)
18.在平面直角坐标系中,直线y=x﹣2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m)出发以每秒个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t= 秒时,⊙P与坐标轴相切.
三、解答题(共78分)
19.(8分)如图,在△ABC中,边BC与⊙A相切于点D,∠BAD=∠CAD.求证:AB=AC.
20.(10分)如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
(1)求证:DE平分∠CDF;
(2)求证:∠ACD=∠AEB.
21.(12分)如图,Rt△ACB中,以BC边上一点O为圆心作圆,⊙O与边AC、AB分别切于点C、D,⊙O与BC另一交点为E.
(1)求证:BD AB=OB BC;
(2)若⊙O的半径为5,AC=,求BD的长.
22.(12分)期末,学校为了调查这学期学生课外阅读情况,随机抽样调查了一部分学生阅读课外书的本数,并将收集到的数据整理成如图的统计图.
(1)这次一共调查的学生人数是 人;
(2)所调查学生读书本数的众数是 本,中位数是 本.
(3)若该校有800名学生,请你估计该校学生这学期读书总数是多少本?
23.(12分)为了解居民对垃圾分类的知晓程度(“A.非常了解”“B.了解”“C.基本了解”“D.不太了解”),佳佳随机调查了若干人.根据调查结果绘制成如下两幅不完整的统计图:
(1)随机调查了 人,扇形统计图中表示“A”的扇形圆心角为 °
(2)补全条形统计图;
(3)估计在10000名市民中基本了解垃圾分类的人数.
24.(12分)如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.
25.(12分)如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=,求⊙O的半径.
答案
一、选择题
1.解:已知⊙O是△ABC的外接圆,那么点O一定是△ABC的三边的垂直平分线的交点,
故选:C.
2.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠B=90°﹣∠C=90°﹣31°=59°.
故选:A.
3.解:300×(40%+15%)=165人,
故选:D.
4.解:弧AE所对的圆周角为∠ABE和∠ACE.
故选:C.
5.解:连接OC.
∵∠COD==60°,OC=OD,
∴△COD是等边三角形,
∴OC=OD=2.
设BC交y轴于G,则∠GOC=30°.
在Rt△GOC中,∵∠GOC=30°,OC=2,
∴GC=1,OG=.
∴C(1,﹣).
故选:C.
6.解:如图,连接OD,OC,
∵AD=DP,
∴OD⊥PA,
∴∠ADO=90°,
∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,
当点D在CK的延长线上时,CD的值最大,
∵C为的三等分点,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴CK⊥OA,
在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,
∴CK==,
∵DK=OA=1,
∴CD=+1,
∴CD的最大值为+1,
故选:D.
二、填空题
7.解:∵圆心O到直线l的距离是2,小于⊙O的半径为4,
∴直线l与⊙O相交.
故答案为:相交.
8.解:∵A、B、C是⊙O上三点,∠ACB=30°,
∴∠AOB的度数是:2∠ACB=60°.
故答案为:60°.
9.解:连接OA,如图,
∵CE=3,DE=7,
∴CD=10,
∴OC=OA=5,OE=2,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==,
∴AB=2AE=2(cm).
故答案为2.
10.解:∵∠APD=∠C+∠A,
∴∠C=65°﹣30°=35°,
∴∠B=∠C=35°.
故答案为35°.
11.解:连结OB,如图,
∵AB与⊙O相切,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∵∠AOB=∠C+∠OBC,
而∠C=∠OBC,
∴∠C=AOB=30°.
故答案为:30°.
12.解:由圆周角定理得,∠COB=2∠A=60°,
∴CE=OC sin∠COE=2×=,
∵AE⊥CD,
∴CD=2CE=2,
故答案为:2,
13.解:估计该区12000名七年级学生视力低于4.8的约有12000×=4800(名),
故答案为:4800名.
14.解:∵∠C=90°,
∴点C在量角器所在的圆上
∵点D对应的刻度读数是54°,即∠AOD=54°,
∴∠ACD=∠AOD=27°,
∴∠BCD=90°﹣27°=63°.
故答案为63.
15.解:如图,连接OE,
∵∠PEF=90°﹣∠OEB=90°﹣∠OBE=∠OFB=∠EFP,
∴PF=PE,
∵AB=6,AB,CD是⊙O的直径,
∴OE=OD=OC=OB=OA=3,
∵PE切⊙O于E,
∴∠PEO=90°,
在Rt△OPE中,DP=2,
OP=3+2=5,
由勾股定理可得OP2=PE2+OE2,
∴52=PE2+32,解得PE=4,
∴PF=PE=4,OF=OP﹣PF=5﹣4=1,
∵AB⊥CD,
∴∠BOF=90°,
在Rt△OBF中,由勾定理可得BF2=OB2+OF2,
即BF2=32+12=10,
∴FB=.
故答案为:.
16.解:连接OA,OB,
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∵OA=OB,
∴∠OAB=∠OBA,
分两种情况:
①当C在优弧AB上时,如图1,
∵∠PAC=α,∠ABC=β,
∴α+β=∠PAC+∠ABC,
=90°+∠OAC+∠ABC,
=90°+∠OAC+180°﹣∠C﹣∠BAC,
=270°+∠OAC﹣AOB﹣∠OAB﹣∠OAC,
=270°﹣﹣∠OAB,
△OAB中,∠AOB+∠OAB+∠OBA=180°,
∴+∠OAB=90°,
∴α+β=270°﹣90°=180°;
②当C在劣弧AB上时,如图2,
∵∠PAO=∠PBO=90°,∠OAB=∠OBA,∠CBP=∠CAB,
∴∠PAC=∠ABC,
即α=β,
综上,α与β的关系是:α+β=180°或α=β;
故答案为:α+β=180°或α=β.
17.解:①2016年的财政收入应该是,故本选项错误;
②因为是正增长,所以2018年比2017年和2016年都高,故本选项错误;
③2019年我国财政收入约为25000(1+11.7%)(1+21.3%)亿元,故本选项正确;
其中正确的有③;
故答案为:③.
18.解:设⊙P与坐标轴的切点为D,
∵直线y=x﹣2与x轴、y轴分别交于点B、C,点A(4,m),
∴x=0时,y=﹣2,y=0时,x=2,x=4时,y=2,
∴A(4,2),B(2,0),C(0,﹣2),
∴AB=2,AC=2,OB=OC=2,
∴△OBC是等腰直角三角形,∠OBC=45°,
①当⊙P与x轴相切时,
∵点D是切点,⊙P的半径是1,
∴PD⊥x轴,PD=1,
∴△BDP是等腰直角三角形,
∴BD=PD=1,PB=,
∴AP=AB﹣PB=,
∵点P的速度为每秒个单位长度,
∴t=1;
②如图,⊙P与x轴和y轴都相切时,
∵PB=,
∴AP=AB+PB=3,
∵点P的速度为每秒个单位长度,
∴t=3;
③当点P只与y轴相切时,
∵PB=,
∴AP=AC+PB=5,
∵点P的速度为每秒个单位长度,
∴t=5.
综上所述,则当t=1或3或5秒时,⊙P与坐标轴相切,
故答案为:1或3或5.
三、解答题
19.解:∵BC与⊙A相切于点D,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(ASA),
∴AB=AC.
20.(1)证明:∵四边形ABCD内接于圆,
∴∠CDE=∠ABC,
由圆周角定理得,∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,
∴∠CAE+∠E=∠ABD+∠DBC,
又∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.
21.(1)证明:连接DO,如图所示.
∵,⊙O与边AC、AB分别切于点C、D,
∴∠ODB=90°=∠ACB.
又∵∠B=∠B,
∴△BDO∽△BCA,
∴=,
∴BD AB=OB BC.
(2)解:设BD=x,则BO==,BC=BO+OC=+5.
∵△BDO∽△BCA,
∴=,即=,
整理,得:7x2﹣120x=0,
解得:x1=,x2=0(舍去,不合题意),
经检验,x=是原方程的解,且符合题意,
∴BD的长为.
22.解:(1)1+1+3+4+6+2+2+1=20,
故答案为:20;
(2)众数是4
中位数是4,;
故答案为:4;4;
(3)每个人读书本数的平均数是:
=(1+2×1+3×3+4×6+5×4+6×2+7×2+8)
=4.5
∴总数是:800×4.5=3600
答:估计该校学生这学期读书总数约3600本.
23.解:(1)150÷30%=500人,360°×30%=108°,
故答案为:500,108;
(2)500×40%=200人,补全条形统计图如图所示:
(3)10000×=2000人,
答:在10000名市民中基本了解垃圾分类的人数为2000人.
24.(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC.
又AB=AC=13,BC=10,D是BC的中点,
∴BD=5.
连接OD;
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线;
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8
∴S阴影=S扇形AOE﹣S△AOE=4π﹣8.
25.(1)证明:连接OB,
∵BE为⊙O的切线,
∴OB⊥BE,
∴∠OBE=90°,
∴∠ABE+∠OBA=90°,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠ABE+∠OAB=90°,
∵AD是⊙O的直径,
∴∠OAB+∠ADB=90°,
∴∠ABE=∠ADB,
∵四边形ABCD的外接圆为⊙O,
∴∠EAB=∠C,
∵∠E=∠DBC,
∴∠ABE=∠BDC,
∴∠ADB=∠BDC,
即DB平分∠ADC;
(2)解:∵tan∠ABE=,
∴设AB=x,则BD=2x,
AD==x,
∵∠E=∠E,∠ABE=∠BDE,
∴△AEB∽△BED,
∴BE2=AE DE,且==,
设AE=a,则BE=2a,
∴4a2=a(a+x),
∴a=x,
∵∠BAE=∠C,∠ABE=∠BDC,
∴△AEB∽△CBD,
∴,
∴=,
解得=3,
∴AD=x=15,
∴OA=.
同课章节目录
