沪科版七年级数学下册试题 13.5 平行线的性质同步习题(含2课时)(含解析)
文档属性
| 名称 | 沪科版七年级数学下册试题 13.5 平行线的性质同步习题(含2课时)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 16:14:36 | ||
图片预览


文档简介
13.5 平行线的性质
第一课时
一、单选题
1.如图,BA//DE,∠B=30°,∠D=40°,则∠C的度数是( )
A.10° B.35° C.70° D.80°
二、填空题
2.如图,AB//CD,则图中_______________°;
3.如图,AEFC是折线,AB//CD,那么∠1,∠2,∠3,∠4的大小所满足的关系式为_______________;
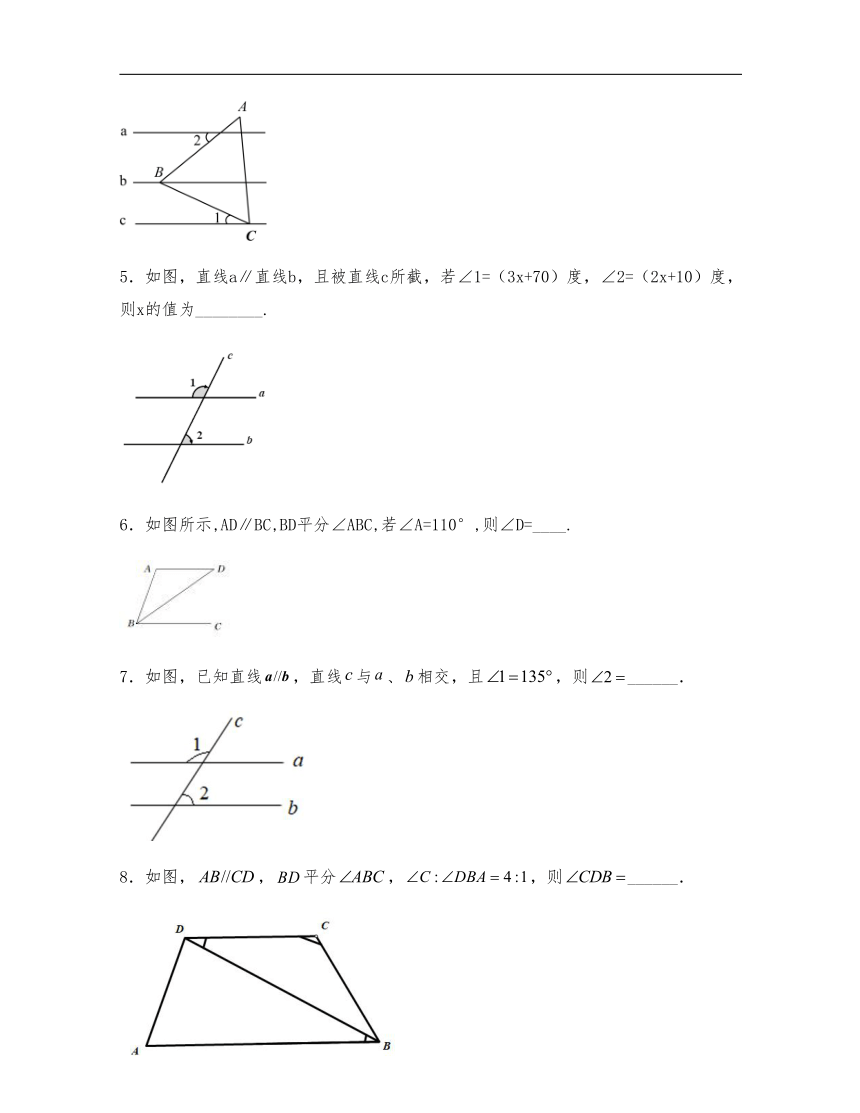
4.如图,已知直线a∥b∥c,△ABC的顶点B、C分别在直线b、c上,如果∠ABC=60°,边BC与直线b的夹角∠1=25°,那么边AB与直线a的夹角∠2=_____度.
5.如图,直线a∥直线b,且被直线c所截,若∠1=(3x+70)度,∠2=(2x+10)度,则x的值为________.
6.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D=____.
7.如图,已知直线,直线与、相交,且,则______.
8.如图,,平分,,则______.
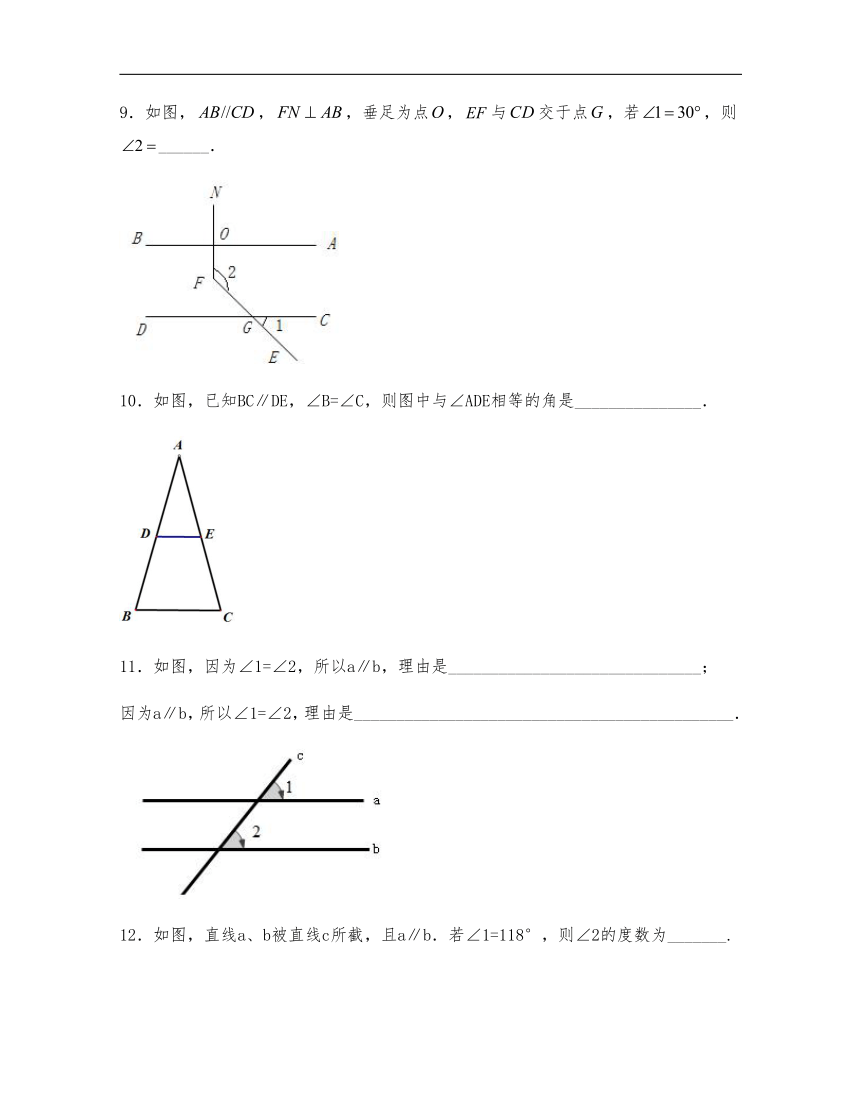
9.如图,,,垂足为点,与交于点,若,则______.
10.如图,已知BC∥DE,∠B=∠C,则图中与∠ADE相等的角是_______________.
11.如图,因为∠1=∠2,所以a∥b,理由是______________________________;
因为a∥b,所以∠1=∠2,理由是_____________________________________________.
12.如图,直线a、b被直线c所截,且a∥b.若∠1=118°,则∠2的度数为_______.
三、解答题
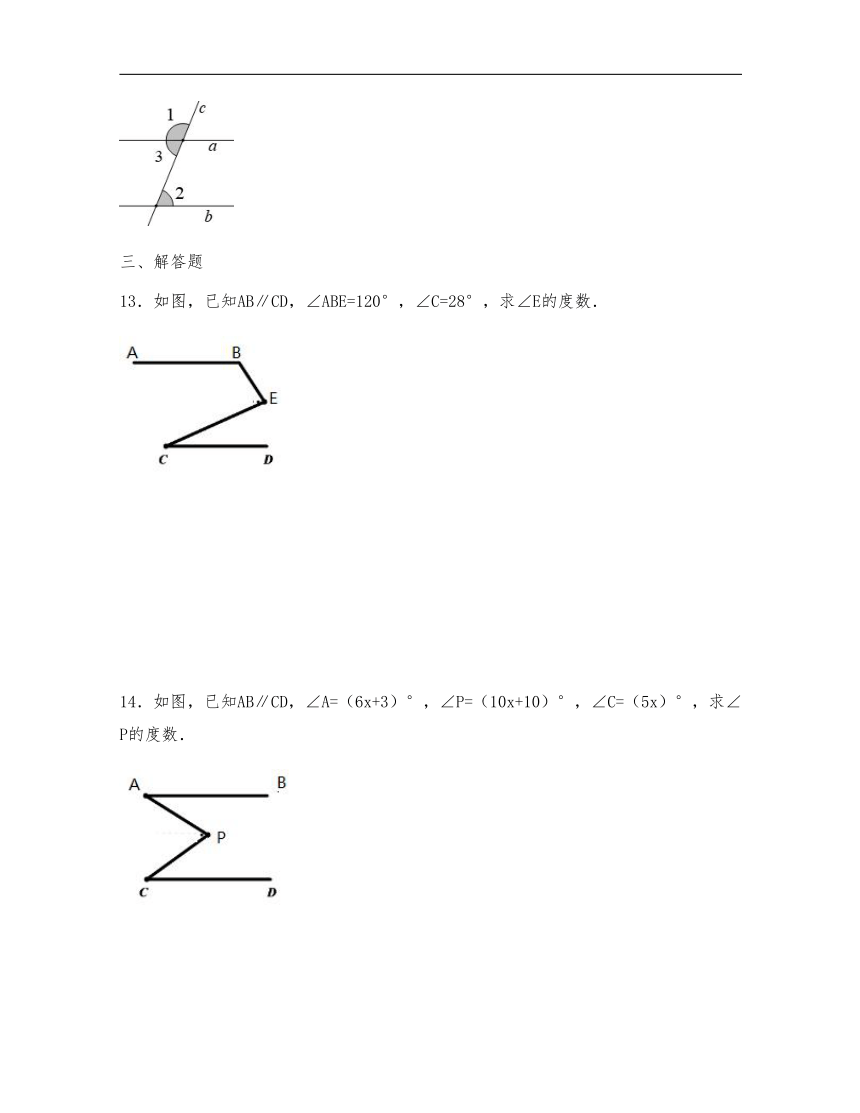
13.如图,已知AB∥CD,∠ABE=120°,∠C=28°,求∠E的度数.
14.如图,已知AB∥CD,∠A=(6x+3)°,∠P=(10x+10)°,∠C=(5x)°,求∠P的度数.
15.如图,已知AB∥DE,那么∠A+∠C+∠D的和是多少度?为什么?
16.如图,AB∥DE,CM平分∠BCE,∠MCN=90°,∠B=50°,求∠DCN的度数.
17.如图,已知直线AB、CD被直线m所截,交点分别为E、F,AB∥CD,且EG平分∠BEF,∠1=40°,求∠2的度数.
18.如图,已知DB∥FG∥EC,∠B=60°,∠C=30°,AP平分∠BAC,求∠PAG的度数.
19.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求∠1和∠2的度数.
第二课时
一、单选题
1.小明、小亮、小刚、小颖一起研究一道数学题.如图,已知,,G是AC边上一点(不与A、C重合),
小明说:“如果还知道,则能得到”;
小亮说:“把小明的已知和结论倒过来,即由,可得到”;
小刚说:“∠AGD一定大于∠ACD”
小颖说:“如果联结GF,则GF一定平行于AB”;
他们四人中,有几个人的说法是正确的?( )
A.1个 B.2个 C.3个 D.4个
二、解答题
2.如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.
解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
3.如图,已知平行四边形ABCD中,AD=BC,AB=DC,其周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.
4.如图,已知AD∥BC,∠B=∠D,那么∠E=∠F?为什么?
5.如图,已知AB∥CD,点E在BC延长线上,联结AE交CD于点F,若∠1=∠2,∠3=∠4,试说明AD∥BE的理由.
6.如图,已知在△ABC中,点D为AC边上一点,DE∥AB交边BC于点E,点F在DE的延长线上,且∠FBE=∠ABD,若∠DEC=∠BDA.
(1)试说明∠BDA=∠ABC的理由;
(2)试说明BF∥AC的理由.
7.如图,已知∠COF+∠C=180°,∠C=∠B.说明AB//EF的理由.
8.如图,已知:,,那么吗?请说明理由?
解:因为(已知),
所以( ).
因为(已知),
所以______=______( ).
所以______∥______( ).
所以( ).
9.如图,已知∠AGB=∠EHF,∠C=∠D,求证:∠A=∠F.
10.如图,已知EF⊥AB,CD⊥AB,垂足分别为E.D,点G在AC上,∠GDC=∠EFB=25°,求∠ADG的度数.
11.如图,已知直线AB∥CD,且∠1=∠2,那么AE与CF平行吗?为什么?说明理由.
12.如图,已知∠1=∠2,∠2=∠3,请写出图中所有互相平行的线,并证明.
13.如图,已知:EG∥AD,∠1=∠G,试说明 AD平分∠BAC.
14.如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G吗?为什么?
解:因为∠BAE+∠AED=180°( 已知)
所以AB∥CD________
所以∠BAE=∠AEC________
因为∠1=∠2( 已知)
所以∠BAE—∠1=∠AEC—∠2(等式性质)
即∠3=∠4
所以AF∥EG________,
所以∠F=∠G________.
15.如图,已知∥.,那么吗?为什么?
第一课时答案
一、单选题
1.C
【分析】根据题意,作出合适的辅助线,然后根据平行线的性质,即可得到∠BCD的度数,本题得以解决.
【详解】解:过点C作FC//AB,
∵BA//DE,
∴BA//DE//FC,
∴∠B=∠BCF,∠D=∠DCF,
∵∠B=30°,∠D=40°,
∴∠BCF=30°,∠DCF=40°,
∴∠BCD=70°,
故选:C.
二、填空题
2.180
【分析】过点E作EF//CD,根据平行线的判定及性质定理即可得证.
【详解】如图:过点E作EF//CD.
∴∠3=∠FEC
∵∠AEF+∠2=∠FEC,
∴∠2+∠AEF=∠3,
∴,
∵AB//CD,EF//CD,
∴EF//AB,
∴∠1+∠AEF=180°
∴.
故答案为:180°
3.或
【分析】首先过点作,过点作,由,即可得,根据两直线平行,内错角相等与两直线平行,同旁内角互补即可求得,,,则可求得、、、的大小所满足的关系式.
【详解】解:过点作,过点作,
,
,
,,,
,,
或.
故答案为:或.
4.35
【分析】根据平行线的性质得到∠ABC=∠2+∠1,即可求解.
【详解】如图,
∵,
∴∠2=∠3,∠1=∠4,
∴∠ABC=∠2+∠1,
∵∠ABC=60°,∠1=25°,
∴∠2=60°﹣25°=35°,
故答案为35.
5.20
【分析】因为两直线平行,所以∠2与∠1的补角互为内错角,通过两直线平行内错角相等,建立一个关于x的方程,解方程即可.
【详解】∵直线a∥直线
∴
即
解得
故答案为20
6.35°
【分析】根据平行线的性质先求得∠ABC的度数,再根据角平分线的性质及平行线的性质求得∠D的度数.
【详解】∵AD∥BC,∠A=110°,
∴∠ABC=180-∠A=70°;
又∵BD平分∠ABC,
∴∠DBC=35°;
∵AD∥BC,
∴∠D=∠DBC=35°.
故答案为:35°.
7.45
【分析】先根据邻补角求出∠3的度数,再根据“两直线平行,同位角相等”求出∠2即可.
【详解】如图,
∵∠1+∠3=180
∴∠3=180 -∠1
∵∠1=135
∴∠3=45
∵a//b
∴∠2=∠3=45 .
故答案为:45
8.30°
【分析】先由AB//CD得到∠CDB=∠ABD,∠C+∠ABC=180 ,设出∠ABD=x°,依据“平分,”列出方程,求出∠ABD即可解决问题.
【详解】∵AB//CD
∴∠ABD=x°,∠ABD,∠C+∠ABC=180 ,
平分,
∴∠ABD=∠CBD
∵,
∴
设∠ABD=x°,则∠CBD=x°,∠C=4x°,
∴2x°+4x°=180°,解得,x=30
∴∠ABD=30°,
∴∠CDB=30°,
故答案为:30°.
9.120°
【分析】过点F作PT//AB,则有PT//CD,根据平行线的性质可得∠GFP=30゜,∠OFP=90゜,从而可求出∠2的度数.
【详解】过点F作PT//AB,如图,
∴∠OFP=∠NOA
∵
∴∠NOA=90゜
∴∠OFP=90゜
∵AB//CD
∴CD//PT
∴∠DGF=∠GFP
∵∠DGF=∠1=30゜
∴∠GFP=30゜
∴∠2=∠OFP+∠GFP=90゜+30゜=120゜
故答案为:120゜
10.∠AED、∠B、∠C
【分析】根据BC∥DE得到∠ADE=∠B,∠AED=∠C,再根据∠B=∠C得到∠ADE=∠AED=∠B=∠C.
【详解】因为BC∥DE,
所以∠ADE=∠B,∠AED=∠C,
又因为∠B=∠C,
所以∠ADE=∠AED=∠B=∠C,
故答案为:∠AED、∠B、∠C.
11.同位角相等,两直线平行 两直线平行,同位角相等
【分析】根据平行线的判定定理和性质定理解答即可.
【详解】由图知∠1与∠2是同位角,
∵∠1=∠2,
∴a∥b,理由是同位角相等,两直线平行;
∵a∥b,
∴∠1=∠2,理由是两直线平行,同位角相等,
故答案为:同位角相等,两直线平行;两直线平行,同位角相等.
12.62°
【解析】∵∠1=118°,
∴∠3=180°-118°=62°.
∵a∥b,
∴∠2=∠3=62°.
三、解答题
13.如图,过点E作
.
14.如图,过点P作,则
,即
解得
则.
15.如图,过点C作,则所求的问题变为的和是多少度
即.
16.解:∵AB∥DE,
∴∠B+∠BCE=180°(两直线平行,同旁内角互补).
∵∠B=50°,
∴∠BCE=180°-50°=130°,
∵CM平分∠BCE,
∴∠ECM= ∠BCE=65°,
∵∠MCN=90°,
∴∠DCN=180°-∠MCN-∠ECM=180°-90°-65°=25°.
17.因为AB∥CD(已知)
所以∠1=∠3(两直线平行,内错角相等)
因为EG平分∠BEF(已知)
所以∠BEF=2∠3(角平分线性质)
所以∠BEF=2∠1(等量代换)
因为∠1=40°(已知)
所以∠BEF=80°
因为AB∥CD(已知)
所以∠2=∠BEF=80°(两直线平行,同位角相等)
18.,
平分
.
19.∵AD∥BC ,
∴∠DEF=∠EFG=55°.
由对称性知∠GEF=∠DEF∠GEF=55°,
∴∠GED=110°.
∵AD∥BC ,
∴∠2=∠GED=110°.
∴∠1=180°-110°=70°,
第二课时答案
一、单选题
1.B
【分析】由,,知,然后根据平行线的性质和判定即可得出答案;
【详解】已知,,
∴,
(1)若,
∵,
∴,
∴,
∴;
(2)若,
∴,
∴,,
∴;
(3)∵DG你一定平行于BC,
∴∠AGD不一定大于∠ACD;
(4)如果连接GF,则GF不一定平行于AB;
综上所述,正确的说法有2个;
故答案选B.
二、解答题
2.∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD(等量代换),
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等.
3.设AB=xcm,则BC=cm
根据平行四边形面积公式得:
列出方程得:
解得:
平行四边形的面积=cm2
4.∵AD∥BC(已知)
∴∠DAB+∠B=180°(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠DAB+∠D=180°(等量代换)
∴DF∥EB(同旁内角互补,两直线平行)
∴∠E=∠F(两直线平行,内错角相等)
5.∵AB∥CD
∴
∵∠1=∠2
∴
∴
∴
∵∠3=∠4
∴
∴
6.(1)理由如下:
∵DE∥AB,
∴∠DEC=∠ABC,
∵∠DEC=∠BDA,
∴∠BDA=∠ABC;
(2)∵∠ABD=∠FBE,
∴∠ABD+∠DBE=∠FBE+∠DBE,
即∠BAC=∠FBD,
∵∠BDA=∠BAC,
∴∠BDA=∠FBD,
∴BF∥AC.
7.解:∵∠COF+∠C=180°,
∴EF//CD,
∵∠C=∠B,
∴AB//CD,
∴AB//EF.
8.
因为(已知),
所以(两直线平行,同位角相等).
因为(已知),
所以_∠1_=_∠DCB_( 等量代换 ).
所以_ DE ∥ BC ( 内错角相等,两直线平行 ).
所以(两直线平行,同位角相等 ).
故答案为:两直线平行,同位角相等;∠1;∠DCB;等量代换;DE;BC;内错角相等,两直线平行;两直线平行,同位角相等.
9.(对顶角相等),
.
10.
在中,
.
11.AE∥CF,理由如下:
因为AB∥CD(已知)
所以∠GAB=∠GCD(同位角相等,两直线平行)
因为∠1=∠2(已知)
所以∠GAB-∠1=∠GCD-∠2,
所以∠GAE=∠GCF(等式性质)
所以AE∥CF(同位角相等,两直线平行).
12.因为∠1=∠2(已知)
所以a∥d(同位角相等,两直线平行)
因为∠2=∠3(已知)
所以b∥d(同位角相等,两直线平行)
所以a∥b∥d(平行线的传递性).
13.∵EG∥AD,
∴∠1=∠2,∠3=∠G,
∵∠G=∠1,
∴∠2=∠3.
∴AD平分∠BAC.
14.解:∵∠BAE+∠AED=180°(已知),∴AB∥CD(同旁内角互补,两直线平行),
∴∠BAE=∠AEC(两直线平行,内错角相等),
∵∠1=∠2(已知),∴∠BAE-∠1=∠AEC-∠2(等式性质),即∠3=∠4,
∴AF∥EG(内错角相等,两直线平行),
∴∠F=∠G(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;两直线平行,内错角相等.
15.解:因为ABCD(已知),
所以∠A=∠EDC(两直线平行,同位角相等).
又因为∠A=∠C(已知),
所以∠C=∠EDC(等量代换).
所以AECF(内错角相等,两直线平行).
那么(两直线平行,内错角相等).
第一课时
一、单选题
1.如图,BA//DE,∠B=30°,∠D=40°,则∠C的度数是( )
A.10° B.35° C.70° D.80°
二、填空题
2.如图,AB//CD,则图中_______________°;
3.如图,AEFC是折线,AB//CD,那么∠1,∠2,∠3,∠4的大小所满足的关系式为_______________;
4.如图,已知直线a∥b∥c,△ABC的顶点B、C分别在直线b、c上,如果∠ABC=60°,边BC与直线b的夹角∠1=25°,那么边AB与直线a的夹角∠2=_____度.
5.如图,直线a∥直线b,且被直线c所截,若∠1=(3x+70)度,∠2=(2x+10)度,则x的值为________.
6.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D=____.
7.如图,已知直线,直线与、相交,且,则______.
8.如图,,平分,,则______.
9.如图,,,垂足为点,与交于点,若,则______.
10.如图,已知BC∥DE,∠B=∠C,则图中与∠ADE相等的角是_______________.
11.如图,因为∠1=∠2,所以a∥b,理由是______________________________;
因为a∥b,所以∠1=∠2,理由是_____________________________________________.
12.如图,直线a、b被直线c所截,且a∥b.若∠1=118°,则∠2的度数为_______.
三、解答题
13.如图,已知AB∥CD,∠ABE=120°,∠C=28°,求∠E的度数.
14.如图,已知AB∥CD,∠A=(6x+3)°,∠P=(10x+10)°,∠C=(5x)°,求∠P的度数.
15.如图,已知AB∥DE,那么∠A+∠C+∠D的和是多少度?为什么?
16.如图,AB∥DE,CM平分∠BCE,∠MCN=90°,∠B=50°,求∠DCN的度数.
17.如图,已知直线AB、CD被直线m所截,交点分别为E、F,AB∥CD,且EG平分∠BEF,∠1=40°,求∠2的度数.
18.如图,已知DB∥FG∥EC,∠B=60°,∠C=30°,AP平分∠BAC,求∠PAG的度数.
19.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求∠1和∠2的度数.
第二课时
一、单选题
1.小明、小亮、小刚、小颖一起研究一道数学题.如图,已知,,G是AC边上一点(不与A、C重合),
小明说:“如果还知道,则能得到”;
小亮说:“把小明的已知和结论倒过来,即由,可得到”;
小刚说:“∠AGD一定大于∠ACD”
小颖说:“如果联结GF,则GF一定平行于AB”;
他们四人中,有几个人的说法是正确的?( )
A.1个 B.2个 C.3个 D.4个
二、解答题
2.如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.
解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
3.如图,已知平行四边形ABCD中,AD=BC,AB=DC,其周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.
4.如图,已知AD∥BC,∠B=∠D,那么∠E=∠F?为什么?
5.如图,已知AB∥CD,点E在BC延长线上,联结AE交CD于点F,若∠1=∠2,∠3=∠4,试说明AD∥BE的理由.
6.如图,已知在△ABC中,点D为AC边上一点,DE∥AB交边BC于点E,点F在DE的延长线上,且∠FBE=∠ABD,若∠DEC=∠BDA.
(1)试说明∠BDA=∠ABC的理由;
(2)试说明BF∥AC的理由.
7.如图,已知∠COF+∠C=180°,∠C=∠B.说明AB//EF的理由.
8.如图,已知:,,那么吗?请说明理由?
解:因为(已知),
所以( ).
因为(已知),
所以______=______( ).
所以______∥______( ).
所以( ).
9.如图,已知∠AGB=∠EHF,∠C=∠D,求证:∠A=∠F.
10.如图,已知EF⊥AB,CD⊥AB,垂足分别为E.D,点G在AC上,∠GDC=∠EFB=25°,求∠ADG的度数.
11.如图,已知直线AB∥CD,且∠1=∠2,那么AE与CF平行吗?为什么?说明理由.
12.如图,已知∠1=∠2,∠2=∠3,请写出图中所有互相平行的线,并证明.
13.如图,已知:EG∥AD,∠1=∠G,试说明 AD平分∠BAC.
14.如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G吗?为什么?
解:因为∠BAE+∠AED=180°( 已知)
所以AB∥CD________
所以∠BAE=∠AEC________
因为∠1=∠2( 已知)
所以∠BAE—∠1=∠AEC—∠2(等式性质)
即∠3=∠4
所以AF∥EG________,
所以∠F=∠G________.
15.如图,已知∥.,那么吗?为什么?
第一课时答案
一、单选题
1.C
【分析】根据题意,作出合适的辅助线,然后根据平行线的性质,即可得到∠BCD的度数,本题得以解决.
【详解】解:过点C作FC//AB,
∵BA//DE,
∴BA//DE//FC,
∴∠B=∠BCF,∠D=∠DCF,
∵∠B=30°,∠D=40°,
∴∠BCF=30°,∠DCF=40°,
∴∠BCD=70°,
故选:C.
二、填空题
2.180
【分析】过点E作EF//CD,根据平行线的判定及性质定理即可得证.
【详解】如图:过点E作EF//CD.
∴∠3=∠FEC
∵∠AEF+∠2=∠FEC,
∴∠2+∠AEF=∠3,
∴,
∵AB//CD,EF//CD,
∴EF//AB,
∴∠1+∠AEF=180°
∴.
故答案为:180°
3.或
【分析】首先过点作,过点作,由,即可得,根据两直线平行,内错角相等与两直线平行,同旁内角互补即可求得,,,则可求得、、、的大小所满足的关系式.
【详解】解:过点作,过点作,
,
,
,,,
,,
或.
故答案为:或.
4.35
【分析】根据平行线的性质得到∠ABC=∠2+∠1,即可求解.
【详解】如图,
∵,
∴∠2=∠3,∠1=∠4,
∴∠ABC=∠2+∠1,
∵∠ABC=60°,∠1=25°,
∴∠2=60°﹣25°=35°,
故答案为35.
5.20
【分析】因为两直线平行,所以∠2与∠1的补角互为内错角,通过两直线平行内错角相等,建立一个关于x的方程,解方程即可.
【详解】∵直线a∥直线
∴
即
解得
故答案为20
6.35°
【分析】根据平行线的性质先求得∠ABC的度数,再根据角平分线的性质及平行线的性质求得∠D的度数.
【详解】∵AD∥BC,∠A=110°,
∴∠ABC=180-∠A=70°;
又∵BD平分∠ABC,
∴∠DBC=35°;
∵AD∥BC,
∴∠D=∠DBC=35°.
故答案为:35°.
7.45
【分析】先根据邻补角求出∠3的度数,再根据“两直线平行,同位角相等”求出∠2即可.
【详解】如图,
∵∠1+∠3=180
∴∠3=180 -∠1
∵∠1=135
∴∠3=45
∵a//b
∴∠2=∠3=45 .
故答案为:45
8.30°
【分析】先由AB//CD得到∠CDB=∠ABD,∠C+∠ABC=180 ,设出∠ABD=x°,依据“平分,”列出方程,求出∠ABD即可解决问题.
【详解】∵AB//CD
∴∠ABD=x°,∠ABD,∠C+∠ABC=180 ,
平分,
∴∠ABD=∠CBD
∵,
∴
设∠ABD=x°,则∠CBD=x°,∠C=4x°,
∴2x°+4x°=180°,解得,x=30
∴∠ABD=30°,
∴∠CDB=30°,
故答案为:30°.
9.120°
【分析】过点F作PT//AB,则有PT//CD,根据平行线的性质可得∠GFP=30゜,∠OFP=90゜,从而可求出∠2的度数.
【详解】过点F作PT//AB,如图,
∴∠OFP=∠NOA
∵
∴∠NOA=90゜
∴∠OFP=90゜
∵AB//CD
∴CD//PT
∴∠DGF=∠GFP
∵∠DGF=∠1=30゜
∴∠GFP=30゜
∴∠2=∠OFP+∠GFP=90゜+30゜=120゜
故答案为:120゜
10.∠AED、∠B、∠C
【分析】根据BC∥DE得到∠ADE=∠B,∠AED=∠C,再根据∠B=∠C得到∠ADE=∠AED=∠B=∠C.
【详解】因为BC∥DE,
所以∠ADE=∠B,∠AED=∠C,
又因为∠B=∠C,
所以∠ADE=∠AED=∠B=∠C,
故答案为:∠AED、∠B、∠C.
11.同位角相等,两直线平行 两直线平行,同位角相等
【分析】根据平行线的判定定理和性质定理解答即可.
【详解】由图知∠1与∠2是同位角,
∵∠1=∠2,
∴a∥b,理由是同位角相等,两直线平行;
∵a∥b,
∴∠1=∠2,理由是两直线平行,同位角相等,
故答案为:同位角相等,两直线平行;两直线平行,同位角相等.
12.62°
【解析】∵∠1=118°,
∴∠3=180°-118°=62°.
∵a∥b,
∴∠2=∠3=62°.
三、解答题
13.如图,过点E作
.
14.如图,过点P作,则
,即
解得
则.
15.如图,过点C作,则所求的问题变为的和是多少度
即.
16.解:∵AB∥DE,
∴∠B+∠BCE=180°(两直线平行,同旁内角互补).
∵∠B=50°,
∴∠BCE=180°-50°=130°,
∵CM平分∠BCE,
∴∠ECM= ∠BCE=65°,
∵∠MCN=90°,
∴∠DCN=180°-∠MCN-∠ECM=180°-90°-65°=25°.
17.因为AB∥CD(已知)
所以∠1=∠3(两直线平行,内错角相等)
因为EG平分∠BEF(已知)
所以∠BEF=2∠3(角平分线性质)
所以∠BEF=2∠1(等量代换)
因为∠1=40°(已知)
所以∠BEF=80°
因为AB∥CD(已知)
所以∠2=∠BEF=80°(两直线平行,同位角相等)
18.,
平分
.
19.∵AD∥BC ,
∴∠DEF=∠EFG=55°.
由对称性知∠GEF=∠DEF∠GEF=55°,
∴∠GED=110°.
∵AD∥BC ,
∴∠2=∠GED=110°.
∴∠1=180°-110°=70°,
第二课时答案
一、单选题
1.B
【分析】由,,知,然后根据平行线的性质和判定即可得出答案;
【详解】已知,,
∴,
(1)若,
∵,
∴,
∴,
∴;
(2)若,
∴,
∴,,
∴;
(3)∵DG你一定平行于BC,
∴∠AGD不一定大于∠ACD;
(4)如果连接GF,则GF不一定平行于AB;
综上所述,正确的说法有2个;
故答案选B.
二、解答题
2.∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD(等量代换),
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;内错角相等,两直线平行;两直线平行,同位角相等.
3.设AB=xcm,则BC=cm
根据平行四边形面积公式得:
列出方程得:
解得:
平行四边形的面积=cm2
4.∵AD∥BC(已知)
∴∠DAB+∠B=180°(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠DAB+∠D=180°(等量代换)
∴DF∥EB(同旁内角互补,两直线平行)
∴∠E=∠F(两直线平行,内错角相等)
5.∵AB∥CD
∴
∵∠1=∠2
∴
∴
∴
∵∠3=∠4
∴
∴
6.(1)理由如下:
∵DE∥AB,
∴∠DEC=∠ABC,
∵∠DEC=∠BDA,
∴∠BDA=∠ABC;
(2)∵∠ABD=∠FBE,
∴∠ABD+∠DBE=∠FBE+∠DBE,
即∠BAC=∠FBD,
∵∠BDA=∠BAC,
∴∠BDA=∠FBD,
∴BF∥AC.
7.解:∵∠COF+∠C=180°,
∴EF//CD,
∵∠C=∠B,
∴AB//CD,
∴AB//EF.
8.
因为(已知),
所以(两直线平行,同位角相等).
因为(已知),
所以_∠1_=_∠DCB_( 等量代换 ).
所以_ DE ∥ BC ( 内错角相等,两直线平行 ).
所以(两直线平行,同位角相等 ).
故答案为:两直线平行,同位角相等;∠1;∠DCB;等量代换;DE;BC;内错角相等,两直线平行;两直线平行,同位角相等.
9.(对顶角相等),
.
10.
在中,
.
11.AE∥CF,理由如下:
因为AB∥CD(已知)
所以∠GAB=∠GCD(同位角相等,两直线平行)
因为∠1=∠2(已知)
所以∠GAB-∠1=∠GCD-∠2,
所以∠GAE=∠GCF(等式性质)
所以AE∥CF(同位角相等,两直线平行).
12.因为∠1=∠2(已知)
所以a∥d(同位角相等,两直线平行)
因为∠2=∠3(已知)
所以b∥d(同位角相等,两直线平行)
所以a∥b∥d(平行线的传递性).
13.∵EG∥AD,
∴∠1=∠2,∠3=∠G,
∵∠G=∠1,
∴∠2=∠3.
∴AD平分∠BAC.
14.解:∵∠BAE+∠AED=180°(已知),∴AB∥CD(同旁内角互补,两直线平行),
∴∠BAE=∠AEC(两直线平行,内错角相等),
∵∠1=∠2(已知),∴∠BAE-∠1=∠AEC-∠2(等式性质),即∠3=∠4,
∴AF∥EG(内错角相等,两直线平行),
∴∠F=∠G(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;两直线平行,内错角相等.
15.解:因为ABCD(已知),
所以∠A=∠EDC(两直线平行,同位角相等).
又因为∠A=∠C(已知),
所以∠C=∠EDC(等量代换).
所以AECF(内错角相等,两直线平行).
那么(两直线平行,内错角相等).
