沪教版七年级数学下册试题 14.4全等三角形的判定同步练习(含答案)
文档属性
| 名称 | 沪教版七年级数学下册试题 14.4全等三角形的判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 590.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 16:37:29 | ||
图片预览




文档简介
14.4全等三角形的判定
第一课时
一、单选题
1.如图用尺规作∠A′O′B′=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
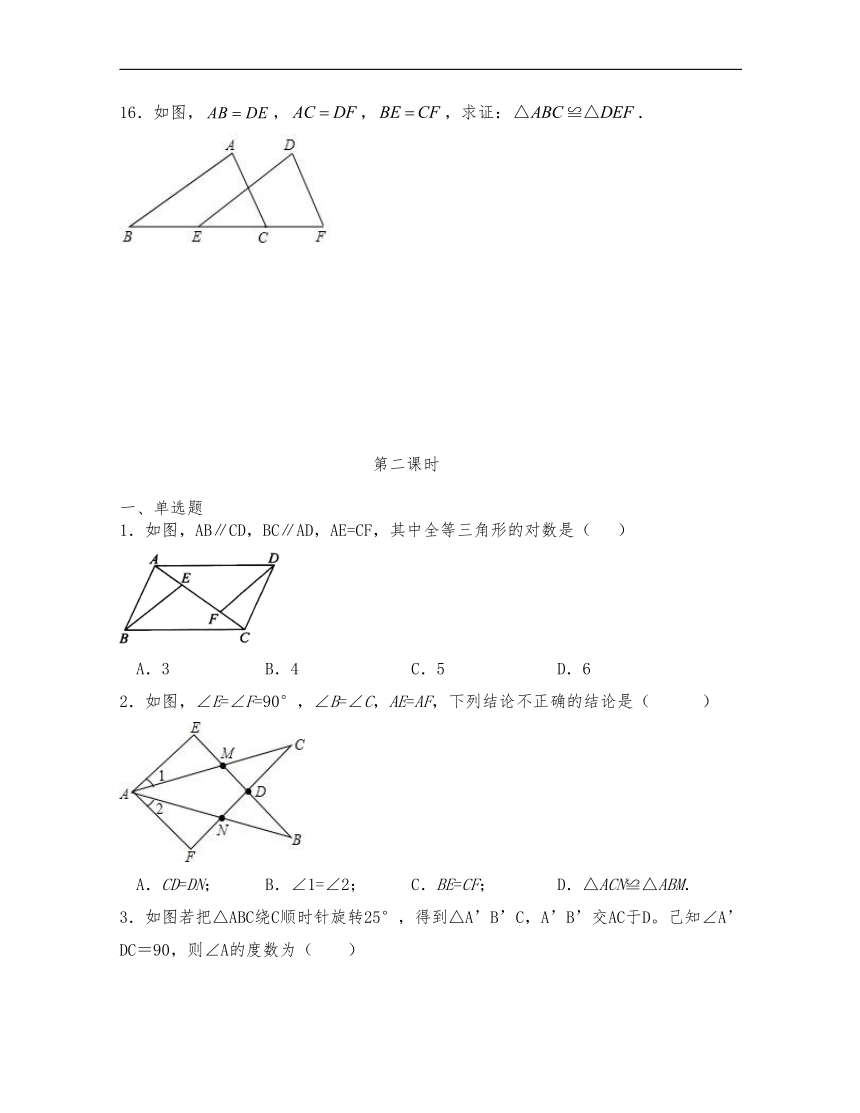
2.如图,,,则的判定依据是( )
A.SSS B.ASA C.AAS D.SAS
3.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
4.如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且,,,,则下列结论中错误的有( )个
①;②;③;④;⑤.
A.1 B.2 C.3 D.4
5.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
6.如图,在中,是上的任意两点.若,则图中阴影部分的面积为( )
A.12 B.20 C.24 D.48
7.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E;其中错误的是( )
A.①② B.②③ C.③④ D.只有④
二、填空题
8.如图,已知AB=AD,那么添加下列一个条件后,能利用“SSS”判定△ABC≌△ADC的是_____.
9.已知如图,AB=AD,请你添加一个适当的条件______________,使△ABC≌△ADC.
10.已知,如图,AD=AC,BD=BC,O为AB上一点,那么图中共有___对全等三角形.
11.如图所示,,,若,则_________.
三、解答题
12.如图,已知点,,,在同一直线上,,,.
求证:.
13.已知:如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,求证:∠A=∠C.
14.如图,.求证:∠A =∠C.
15.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:
(1);
(2).
16.如图,,,,求证:.
第二课时
一、单选题
1.如图,AB∥CD,BC∥AD,AE=CF,其中全等三角形的对数是( )
A.3 B.4 C.5 D.6
2.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
A.CD=DN; B.∠1=∠2; C.BE=CF; D.△ACN≌△ABM.
3.如图若把△ABC绕C顺时针旋转25°,得到△A’B’C,A’B’交AC于D。己知∠A’DC=90,则∠A的度数为( )
A.45° B.55° C.65° D.25°
4.如图,在△ABC与△DEF中,给出下列六个条件:(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个条件为已知,不能判断△ABC与△DEF全等的是( )
A.(1)(2)(3) B.(1)(2)(5)
C.(1)(4)(6) D.(2)(3)(4)
5.如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
A.2对 B.3对 C.4对 D.5对
6.下列选项所给条件能画出唯一的是( )
A.,, B.,,
C., D.,,
二、填空题
7.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
8.如图:在中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.
解:因为AB=AC,AD⊥BC(已知)
所以BD=
因为CE∥BF(已知)
所以=
在中,
中
=
=
所以( )
所以DE=DF( )
9.如图,已知AB=DB,∠1=∠2,请添加一个适当的条件,__________________使△ABC≌△DBE,并使其判定依据为SAS
三、解答题
10.如图,中,,、、分别在、、上,且,
求证:.
证明:∵( ),
且(如图所示),
∴(等量代换)
又∵(已知),
∴________________(等式性质).
在与中,
∴( )
∴( ).
11.阅读并填空:如图,已知在中,,点在边上,且,说明的理由.
解:因为,
所以_______________(等边对等角).
因为_______________,
所以(等边对等角).
在与中,
所以(_______________)
所以_______________(全等三角形对应边相等),
所以_______________(等式性质).
12.如图,在△ABC中,已知点D,E,F分别在边BC,AC,AB上,且FD=DE,BF=CD,∠FDE=∠B,请判断△ABC的形状(按边分)?并说明理由
13.画图题:
(1)画△ABC,使BC=5cm,∠B=45°,∠C=60°;
(2)画出(1)中△ABC的角平分线AD(尺规作图,保留作图痕迹)
14.如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
第一课时答案
一、单选题
1.D
【分析】由作图可知,,,根据证明三角形全等即可解决问题,
【详解】解:由作图可知,,,
△,.故选:.
2.A
【分析】利用SSS定理进行判定即可.
【详解】解:∵,,AB=AB
∴(SSS)
故选:A.
3.A
【分析】根据已知条件利用“边边边”证明△MOC≌△NOC,即可求解.
【详解】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
4.A
【分析】由SSS证明△ABC≌△DEF得出∠B=∠DEF,∠ACB=∠F,BC=EF=5,证出AB∥DE,得出CF=EF EC=3,由三角形内角和定理得出∠F=∠ACB=35°,即可得出答案.
【详解】解:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS)
∴∠B=∠DEF,∠ACB=∠F,BC=EF=5,
∴AB∥DE,AC∥DF,
∵EC=2,
∴CF=EF EC=5-2=3,
∵∠ACB=180° ∠A ∠B=180° 70° 75°=35°,
∴∠F=35°,
即选项①②④⑤正确,选项③错误;
故选:A.
5.C
试题分析:AB=AD,CB=CD,AC=AC所以 ABC ACD,所以∠B=∠D=30°,因为∠BAD=46°,所以∠CAD=23°,所以∠ACD=180°-30°-23°=127°,故选C.
6.A
【分析】利用SSS证明△ADC≌△ADB,可得S△ADC=S△ADB,通过拼接可得S阴影=S△ADB,再利用三角形的面积公式可求解.
【详解】∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),AD⊥BC
∴S△ADC=S△ADB,BD=BC,
∵BC=8,
∴BD=4,
∵S△BEF=S△CEF,AD=6,
∴S阴影=S△ADB=BD AD×4×6=12.
故选:A.
7.D
【详解】解:因为AE=AD,AB=AC,EC=DB;
所以△ABD≌△ACE(SSS);
所以∠C=∠B,∠D=∠E,∠EAC=∠DAB;
所以 ∠EAC-∠DAC=∠DAB-∠DAC;
得∠EAD=∠CAB.
所以错误的结论是④,
故选D.
二、填空题
8.CB=CD
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,则由题意根据SSS可添加CB=CD.
【详解】已知AB=AD,AC是公共边,具备了两组边对应相等,则由题意根据SSS能判定△ABC≌△ADC,则需添加CB=CD,故答案为:CB=CD.
9.BC=DC
【分析】根据全等三角形的判定即可写出.
【详解】∵AB=AD,AC=AC,故添加BC=DC,利用SSS证明△ABC≌△ADC,
故填:BC=DC.
10.3
试题分析:由已知条件,结合图形可得△ADB≌△ACB,△ACO≌△ADO,△CBO≌△DBO共3对.找寻时要由易到难,逐个验证.
试题解析:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为3.
11.
【分析】连接AD,根据SSS证明△ABD≌△ACD,再根据全等三角形的性质得出.
【详解】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
三、解答题
12.∵,
∴BE+EC=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠F,
∴.
13.如图,连结OE
在△OEA和△OEC中
∴△OEA≌△OEC(SSS)
∴∠A=∠C(全等三角形的对应角相等)
14.在和中,
.
15.(1)∵,
∴,即,
在△ABC与△DEF中,
,
∴;
(2)∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
∴∠A=∠EGC.
16.解:∵,
∴,
即,
在和中,
∵,
∴.
第二课时答案
一、单选题
1.A
【分析】根据平行线的性质求出∠BAC=∠DCA,∠ACB=∠DAC,根据ASA推出△△BAC≌△DCA,根据全等三角形的对应边相等得出AD=BC,AB=CD,再根据SAS推出△ABE≌△CDF,根据全等三角形的对应边相等得出BE=DF,求出AF=CE,根据SSS推出△ADF≌△CBE即可.
【详解】∵AB∥CD,BC∥AD,
∴∠BAC=∠DCA,∠ACB=∠DAC.
在△ABC和△CDA中,
∴△BAC≌△DCA(ASA),∴AD=BC,AB=CD.
在△ABE和△CDF中,∴△ABE≌△CDF(SAS),∴BE=DF.
∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,
在△ADF和△CBE中,∴△ADF≌△CBE(SSS),
即3对全等三角形,故选A.
2.A
【分析】利用“角角边”证明△ABE和△ACF全等,根据全等三角形对应角相等可得∠BAE=∠CAF,然后求出∠1=∠2,全等三角形对应边相等可得BE=CF,AB=AC,再利用“角边角”证明△ACN和△ABM全等.
【详解】在△ABE和△ACF中, ,∴△ABE≌△ACF(AAS),
∴∠BAE=∠CAF,BE=CF,AB=AC,故C选项结论正确;
∴∠BAE-∠BAC=∠CAF-∠BAC,即∠1=∠2,故B选项结论正确;
在△ACN和△ABM中, ,∴△ACN≌△ABM(ASA),故D选项结论正确;
CD与DN的大小无法确定,故A选项结论错误.故选A.
3.C
【分析】根据图形的旋转不改变图形的形状,确定∠ACA′=25°,然后再利用直角三角形两锐角互余,即可求解。
【详解】解:∵△ABC绕点C顺时针旋转25°,得到△A′B′C,∴∠ACA′=25°,
又∵∠A′DC=90°,∴∠A′=90°-25°=65°,∴∠A=65°.故答案为C.
4.D
【分析】根据三角形全等的判定方法对各选项分析判断利用排除法求解.
【详解】A、(1)(2)(3)符合“SSS”,能判断△ABC与△DEF全等,故本选项错误;
B、(1)(5)(2)符合“SAS”,能判断△ABC与△DEF全等,故本选项错误;
C、(4)(6)(1)符合“AAS”,能判断△ABC与△DEF全等,故本选项错误;
D、(2)(3)(4),是边边角,不能判断△ABC与△DEF全等,故本选项正确.
故选D.
5.C
【分析】由条件可证△AOD≌△BOC,可得∠A=∠B,则可证明△ACE≌△BDE,可得AE=BE,则可证明△AOE≌△BOE,可得∠COE=∠DOE,可证△COE≌△DOE,可求得答案.
【详解】解:
在△AOD和△BOC中,∴△AOD≌△BOC(SAS),∴∠A=∠B,
∵OC=OD,OA=OB,∴AC=BD,
在△ACE和△BDE中
∴△ACE≌△BDE(AAS),∴AE=BE,
在△AOE和△BOE中,∴△AOE≌△BOE(SAS),∴∠COE=∠DOE,
在△COE和△DOE中,∴△COE≌△DOE(SAS),
故全等的三角形有4对,故选C.
6.A
【解析】A中两角夹一边,形状固定,所以可作唯一三角形;B中∠B并不是AB,AC的夹角,所以可画出多个三角形;C中两个锐角也不确定,也可画出多个三角形;D中AC与BC两边之差大于第三边,所以不能作出三角形,
故选A.
二、填空题
7.①②④③,①④③②.
【分析】根据已知条件,根据三角形全等的判定方法,结合条件在图形上的位置进行选择能够判定三角形全等的条件,另一个作为结论,可得答案.
【详解】解:(1)①②④ ③.
证明如下:∵DE=DC,DA=DB,AC=BE,∴△DCA≌△DEB(SSS)
∴∠C=∠E(全等三角形的对应角相等)
(2) ①④③ ②
证明如下:∵,,
∴△DCA≌△DEB(SAS)
∴DA=DB(全等三角形的对应边相等)
故答案为:①②④ ③,①④③ ②.
8.CD,∠F,,BD=CD.,AAS,全等三角形对应边相等.
【分析】据已知条件判定两三角形全等并利用全等三角形的对应边相等得到线段DE-DF的长即可;
【详解】解:∵AB=AC,AD⊥BC(已知)
∴BD=CD.
∵CE∥ BF
.∴∠CED=∠F,∠EDC=∠BDF(对顶角相等)
在△BFD和△CED中
∴△BFD≌△CED(AAS)
∴DE=DF(全等三角形对应边相等).
故答案为:CD,∠F,,BD=CD.,AAS,全等三角形对应边相等.
9.BC=BE.
【分析】要使△ABC≌△DBE,已知AB=DB,由∠1=∠2得∠ABC=∠DBE,具备了一组边和一组角对应相等,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.
【详解】∵∠1=∠2,∴∠ABC=∠DBE,又AB=DB,
∴根据SAS判定△ABC≌△DBE添加BC=BE;故答案为:BC=BE.
三、解答题
10.证明:∵(三角形的一个外角等于与它不相邻的两个外角的和),
且(如图所示),
∴(等量代换)
又∵(已知),
∴(等式性质).
在与中,
∴(ASA)
∴(全等三角形的对应边相等).
故答案依次为:三角形的一个外角等于与它不相邻的两个外角的和,,,,全等三角形的对应边相等
11.因为,
所以∠B=∠C(等边对等角),
因为AD=AE,
所以(等边对等角).
在与中,
,
所以(AAS),
所以BE=CD(全等三角形对应边相等),
所以BD=CE(等式性质),
故答案为:.
2.因为∠FDC=∠B+∠1,
即∠FDE+∠2=∠B+∠1.
又因为∠FDE=∠B,所以∠1=∠2.
在△DFB和△EDC中,
, 所以△DFB≌△EDC(SAS).因此∠B=∠C.
所以,△ABC是等腰三角形.
13.(1)如图所示:
(2)如图所示:
14.(1)证明:如图,
∵AE⊥AD,
∴∠DAE=∠DAC+∠2=90°,
又∵∠BAC=∠DAC+∠1=90°,
∴∠1=∠2,
在△ABD和△ACE中
,
∴△ABD≌△ACE.
(2)结论:BD2+FC2=DF2.理由如下:
连接FE,∵∠BAC=90°,AB=AC,
∴∠B=∠3=45°
由(1)知△ABD≌△ACE
∴∠4=∠B=45°,BD=CE
∴∠ECF=∠3+∠4=90°,
∴CE2+CF2=EF2,
∴BD2+FC2=EF2,
∵AF平分∠DAE,
∴∠DAF=∠EAF,
在△DAF和△EAF中
,
∴△DAF≌△EAF
∴DF=EF
∴BD2+FC2=DF2.
第一课时
一、单选题
1.如图用尺规作∠A′O′B′=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
2.如图,,,则的判定依据是( )
A.SSS B.ASA C.AAS D.SAS
3.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
4.如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且,,,,则下列结论中错误的有( )个
①;②;③;④;⑤.
A.1 B.2 C.3 D.4
5.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
6.如图,在中,是上的任意两点.若,则图中阴影部分的面积为( )
A.12 B.20 C.24 D.48
7.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E;其中错误的是( )
A.①② B.②③ C.③④ D.只有④
二、填空题
8.如图,已知AB=AD,那么添加下列一个条件后,能利用“SSS”判定△ABC≌△ADC的是_____.
9.已知如图,AB=AD,请你添加一个适当的条件______________,使△ABC≌△ADC.
10.已知,如图,AD=AC,BD=BC,O为AB上一点,那么图中共有___对全等三角形.
11.如图所示,,,若,则_________.
三、解答题
12.如图,已知点,,,在同一直线上,,,.
求证:.
13.已知:如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,求证:∠A=∠C.
14.如图,.求证:∠A =∠C.
15.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:
(1);
(2).
16.如图,,,,求证:.
第二课时
一、单选题
1.如图,AB∥CD,BC∥AD,AE=CF,其中全等三角形的对数是( )
A.3 B.4 C.5 D.6
2.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
A.CD=DN; B.∠1=∠2; C.BE=CF; D.△ACN≌△ABM.
3.如图若把△ABC绕C顺时针旋转25°,得到△A’B’C,A’B’交AC于D。己知∠A’DC=90,则∠A的度数为( )
A.45° B.55° C.65° D.25°
4.如图,在△ABC与△DEF中,给出下列六个条件:(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个条件为已知,不能判断△ABC与△DEF全等的是( )
A.(1)(2)(3) B.(1)(2)(5)
C.(1)(4)(6) D.(2)(3)(4)
5.如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
A.2对 B.3对 C.4对 D.5对
6.下列选项所给条件能画出唯一的是( )
A.,, B.,,
C., D.,,
二、填空题
7.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
8.如图:在中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.
解:因为AB=AC,AD⊥BC(已知)
所以BD=
因为CE∥BF(已知)
所以=
在中,
中
=
=
所以( )
所以DE=DF( )
9.如图,已知AB=DB,∠1=∠2,请添加一个适当的条件,__________________使△ABC≌△DBE,并使其判定依据为SAS
三、解答题
10.如图,中,,、、分别在、、上,且,
求证:.
证明:∵( ),
且(如图所示),
∴(等量代换)
又∵(已知),
∴________________(等式性质).
在与中,
∴( )
∴( ).
11.阅读并填空:如图,已知在中,,点在边上,且,说明的理由.
解:因为,
所以_______________(等边对等角).
因为_______________,
所以(等边对等角).
在与中,
所以(_______________)
所以_______________(全等三角形对应边相等),
所以_______________(等式性质).
12.如图,在△ABC中,已知点D,E,F分别在边BC,AC,AB上,且FD=DE,BF=CD,∠FDE=∠B,请判断△ABC的形状(按边分)?并说明理由
13.画图题:
(1)画△ABC,使BC=5cm,∠B=45°,∠C=60°;
(2)画出(1)中△ABC的角平分线AD(尺规作图,保留作图痕迹)
14.如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
第一课时答案
一、单选题
1.D
【分析】由作图可知,,,根据证明三角形全等即可解决问题,
【详解】解:由作图可知,,,
△,.故选:.
2.A
【分析】利用SSS定理进行判定即可.
【详解】解:∵,,AB=AB
∴(SSS)
故选:A.
3.A
【分析】根据已知条件利用“边边边”证明△MOC≌△NOC,即可求解.
【详解】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
4.A
【分析】由SSS证明△ABC≌△DEF得出∠B=∠DEF,∠ACB=∠F,BC=EF=5,证出AB∥DE,得出CF=EF EC=3,由三角形内角和定理得出∠F=∠ACB=35°,即可得出答案.
【详解】解:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS)
∴∠B=∠DEF,∠ACB=∠F,BC=EF=5,
∴AB∥DE,AC∥DF,
∵EC=2,
∴CF=EF EC=5-2=3,
∵∠ACB=180° ∠A ∠B=180° 70° 75°=35°,
∴∠F=35°,
即选项①②④⑤正确,选项③错误;
故选:A.
5.C
试题分析:AB=AD,CB=CD,AC=AC所以 ABC ACD,所以∠B=∠D=30°,因为∠BAD=46°,所以∠CAD=23°,所以∠ACD=180°-30°-23°=127°,故选C.
6.A
【分析】利用SSS证明△ADC≌△ADB,可得S△ADC=S△ADB,通过拼接可得S阴影=S△ADB,再利用三角形的面积公式可求解.
【详解】∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),AD⊥BC
∴S△ADC=S△ADB,BD=BC,
∵BC=8,
∴BD=4,
∵S△BEF=S△CEF,AD=6,
∴S阴影=S△ADB=BD AD×4×6=12.
故选:A.
7.D
【详解】解:因为AE=AD,AB=AC,EC=DB;
所以△ABD≌△ACE(SSS);
所以∠C=∠B,∠D=∠E,∠EAC=∠DAB;
所以 ∠EAC-∠DAC=∠DAB-∠DAC;
得∠EAD=∠CAB.
所以错误的结论是④,
故选D.
二、填空题
8.CB=CD
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,则由题意根据SSS可添加CB=CD.
【详解】已知AB=AD,AC是公共边,具备了两组边对应相等,则由题意根据SSS能判定△ABC≌△ADC,则需添加CB=CD,故答案为:CB=CD.
9.BC=DC
【分析】根据全等三角形的判定即可写出.
【详解】∵AB=AD,AC=AC,故添加BC=DC,利用SSS证明△ABC≌△ADC,
故填:BC=DC.
10.3
试题分析:由已知条件,结合图形可得△ADB≌△ACB,△ACO≌△ADO,△CBO≌△DBO共3对.找寻时要由易到难,逐个验证.
试题解析:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为3.
11.
【分析】连接AD,根据SSS证明△ABD≌△ACD,再根据全等三角形的性质得出.
【详解】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
三、解答题
12.∵,
∴BE+EC=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠F,
∴.
13.如图,连结OE
在△OEA和△OEC中
∴△OEA≌△OEC(SSS)
∴∠A=∠C(全等三角形的对应角相等)
14.在和中,
.
15.(1)∵,
∴,即,
在△ABC与△DEF中,
,
∴;
(2)∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
∴∠A=∠EGC.
16.解:∵,
∴,
即,
在和中,
∵,
∴.
第二课时答案
一、单选题
1.A
【分析】根据平行线的性质求出∠BAC=∠DCA,∠ACB=∠DAC,根据ASA推出△△BAC≌△DCA,根据全等三角形的对应边相等得出AD=BC,AB=CD,再根据SAS推出△ABE≌△CDF,根据全等三角形的对应边相等得出BE=DF,求出AF=CE,根据SSS推出△ADF≌△CBE即可.
【详解】∵AB∥CD,BC∥AD,
∴∠BAC=∠DCA,∠ACB=∠DAC.
在△ABC和△CDA中,
∴△BAC≌△DCA(ASA),∴AD=BC,AB=CD.
在△ABE和△CDF中,∴△ABE≌△CDF(SAS),∴BE=DF.
∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,
在△ADF和△CBE中,∴△ADF≌△CBE(SSS),
即3对全等三角形,故选A.
2.A
【分析】利用“角角边”证明△ABE和△ACF全等,根据全等三角形对应角相等可得∠BAE=∠CAF,然后求出∠1=∠2,全等三角形对应边相等可得BE=CF,AB=AC,再利用“角边角”证明△ACN和△ABM全等.
【详解】在△ABE和△ACF中, ,∴△ABE≌△ACF(AAS),
∴∠BAE=∠CAF,BE=CF,AB=AC,故C选项结论正确;
∴∠BAE-∠BAC=∠CAF-∠BAC,即∠1=∠2,故B选项结论正确;
在△ACN和△ABM中, ,∴△ACN≌△ABM(ASA),故D选项结论正确;
CD与DN的大小无法确定,故A选项结论错误.故选A.
3.C
【分析】根据图形的旋转不改变图形的形状,确定∠ACA′=25°,然后再利用直角三角形两锐角互余,即可求解。
【详解】解:∵△ABC绕点C顺时针旋转25°,得到△A′B′C,∴∠ACA′=25°,
又∵∠A′DC=90°,∴∠A′=90°-25°=65°,∴∠A=65°.故答案为C.
4.D
【分析】根据三角形全等的判定方法对各选项分析判断利用排除法求解.
【详解】A、(1)(2)(3)符合“SSS”,能判断△ABC与△DEF全等,故本选项错误;
B、(1)(5)(2)符合“SAS”,能判断△ABC与△DEF全等,故本选项错误;
C、(4)(6)(1)符合“AAS”,能判断△ABC与△DEF全等,故本选项错误;
D、(2)(3)(4),是边边角,不能判断△ABC与△DEF全等,故本选项正确.
故选D.
5.C
【分析】由条件可证△AOD≌△BOC,可得∠A=∠B,则可证明△ACE≌△BDE,可得AE=BE,则可证明△AOE≌△BOE,可得∠COE=∠DOE,可证△COE≌△DOE,可求得答案.
【详解】解:
在△AOD和△BOC中,∴△AOD≌△BOC(SAS),∴∠A=∠B,
∵OC=OD,OA=OB,∴AC=BD,
在△ACE和△BDE中
∴△ACE≌△BDE(AAS),∴AE=BE,
在△AOE和△BOE中,∴△AOE≌△BOE(SAS),∴∠COE=∠DOE,
在△COE和△DOE中,∴△COE≌△DOE(SAS),
故全等的三角形有4对,故选C.
6.A
【解析】A中两角夹一边,形状固定,所以可作唯一三角形;B中∠B并不是AB,AC的夹角,所以可画出多个三角形;C中两个锐角也不确定,也可画出多个三角形;D中AC与BC两边之差大于第三边,所以不能作出三角形,
故选A.
二、填空题
7.①②④③,①④③②.
【分析】根据已知条件,根据三角形全等的判定方法,结合条件在图形上的位置进行选择能够判定三角形全等的条件,另一个作为结论,可得答案.
【详解】解:(1)①②④ ③.
证明如下:∵DE=DC,DA=DB,AC=BE,∴△DCA≌△DEB(SSS)
∴∠C=∠E(全等三角形的对应角相等)
(2) ①④③ ②
证明如下:∵,,
∴△DCA≌△DEB(SAS)
∴DA=DB(全等三角形的对应边相等)
故答案为:①②④ ③,①④③ ②.
8.CD,∠F,,BD=CD.,AAS,全等三角形对应边相等.
【分析】据已知条件判定两三角形全等并利用全等三角形的对应边相等得到线段DE-DF的长即可;
【详解】解:∵AB=AC,AD⊥BC(已知)
∴BD=CD.
∵CE∥ BF
.∴∠CED=∠F,∠EDC=∠BDF(对顶角相等)
在△BFD和△CED中
∴△BFD≌△CED(AAS)
∴DE=DF(全等三角形对应边相等).
故答案为:CD,∠F,,BD=CD.,AAS,全等三角形对应边相等.
9.BC=BE.
【分析】要使△ABC≌△DBE,已知AB=DB,由∠1=∠2得∠ABC=∠DBE,具备了一组边和一组角对应相等,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.
【详解】∵∠1=∠2,∴∠ABC=∠DBE,又AB=DB,
∴根据SAS判定△ABC≌△DBE添加BC=BE;故答案为:BC=BE.
三、解答题
10.证明:∵(三角形的一个外角等于与它不相邻的两个外角的和),
且(如图所示),
∴(等量代换)
又∵(已知),
∴(等式性质).
在与中,
∴(ASA)
∴(全等三角形的对应边相等).
故答案依次为:三角形的一个外角等于与它不相邻的两个外角的和,,,,全等三角形的对应边相等
11.因为,
所以∠B=∠C(等边对等角),
因为AD=AE,
所以(等边对等角).
在与中,
,
所以(AAS),
所以BE=CD(全等三角形对应边相等),
所以BD=CE(等式性质),
故答案为:.
2.因为∠FDC=∠B+∠1,
即∠FDE+∠2=∠B+∠1.
又因为∠FDE=∠B,所以∠1=∠2.
在△DFB和△EDC中,
, 所以△DFB≌△EDC(SAS).因此∠B=∠C.
所以,△ABC是等腰三角形.
13.(1)如图所示:
(2)如图所示:
14.(1)证明:如图,
∵AE⊥AD,
∴∠DAE=∠DAC+∠2=90°,
又∵∠BAC=∠DAC+∠1=90°,
∴∠1=∠2,
在△ABD和△ACE中
,
∴△ABD≌△ACE.
(2)结论:BD2+FC2=DF2.理由如下:
连接FE,∵∠BAC=90°,AB=AC,
∴∠B=∠3=45°
由(1)知△ABD≌△ACE
∴∠4=∠B=45°,BD=CE
∴∠ECF=∠3+∠4=90°,
∴CE2+CF2=EF2,
∴BD2+FC2=EF2,
∵AF平分∠DAE,
∴∠DAF=∠EAF,
在△DAF和△EAF中
,
∴△DAF≌△EAF
∴DF=EF
∴BD2+FC2=DF2.
