数学:1.1.1《正弦定理》课件(新人教b版必修5)
文档属性
| 名称 | 数学:1.1.1《正弦定理》课件(新人教b版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览




文档简介
课件18张PPT。2019/3/131.1.1 正弦定理 课件2019/3/13
1、边的关系:2、角的关系:3、边角关系:1)两边之和大于第三边;两边之差小于第三边2)在直角三角形中:a2+b2=c21)A+B+C=18001)大边对大角,大角对大边,等边对等角2)在直角三角形ABC中,C=900,则回顾三角形中的边角关系:一、前提测评2019/3/131、知识目标
(1)使同学们理解正弦定理的推导过程
(2)能应用正弦定理解斜三角形
2、能力目标
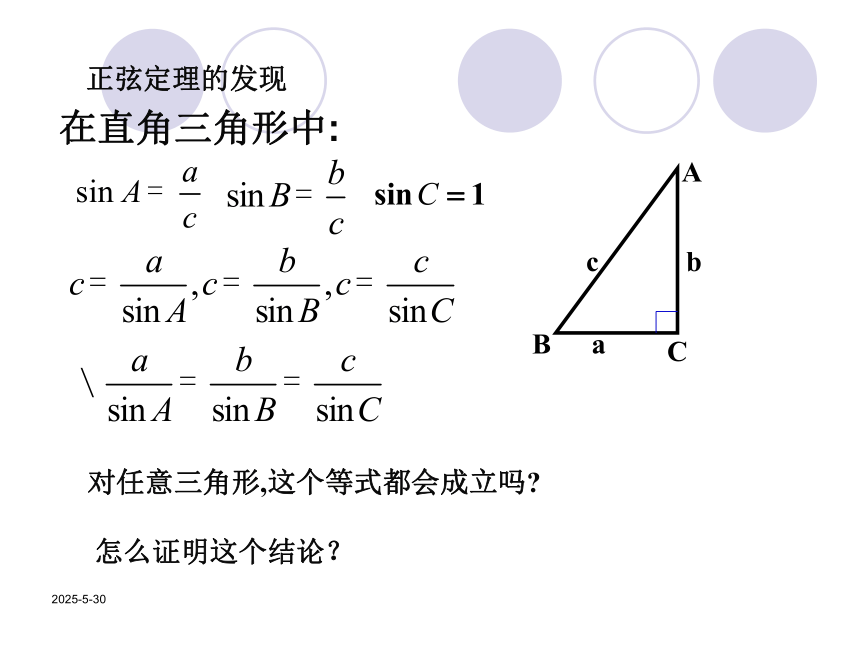
培养同学们分析归纳的能力、分析问题解决问题的能力二、展示目标2019/3/13对任意三角形,这个等式都会成立吗?怎么证明这个结论?正弦定理的发现
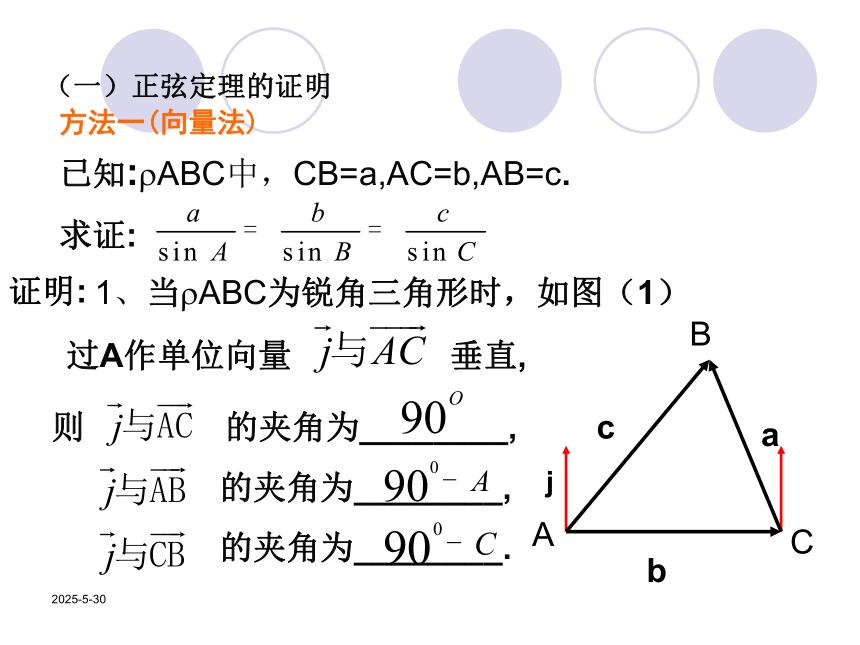
2019/3/131、当?ABC为锐角三角形时,如图(1)证明:过A作单位向量 垂直,则 的夹角为________,
的夹角为________,
的夹角为________.已知:?ABC中,CB=a,AC=b,AB=c.
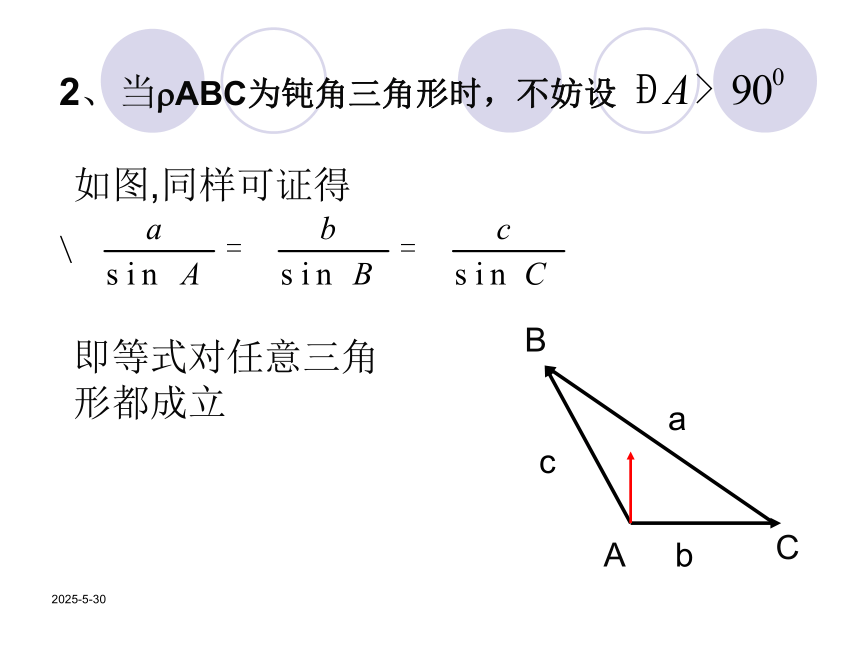
求证:方法一(向量法)(一)正弦定理的证明2019/3/132019/3/132、当?ABC为钝角三角形时,不妨设如图,同样可证得即等式对任意三角形都成立2019/3/13证法二:(等积法)在任意斜?ABC当中
作AD⊥BC于D ∴∵∴同理可证D2019/3/13证法三:(外接圆法)如图所示,作?ABC外接圆则∴同理D∠A=∠D2019/3/13正弦定理在任意一个三角形中,各边和它所对角的正弦的比相等,即注意:定理适合任意三角形。(2R是三角形外接圆的直径)2019/3/13正弦定理在解斜三角形中的两类应用:(1)、已知两角和任一边,求一角和其他两条边.(2)、已知两边和其中一边的对角,求另一边的对角(进而求其他的角和边)2019/3/13例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B 解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050 由 = 得 a= = =10由 =
得 b= = = 20sin750=20×
= 5 +5例题讲解:2019/3/13例2、在ΔABC中,b= ,B=600 ,c=1,求a和A,C 解:∵ = ∴ sinC= = =
∴ B=900 a= =2 ∵b>c,B=600 ∴C求b和B、C 解:∵ = ∴ sinC= =sinC= =
b= = = +1∴C=600∴当C=600时,B=750 或C=12002019/3/13∴当C=1200 时,B=150 ,
b= = = -1
∴b= +1, B=750 ,C=600
或b= -1, B=150 ,C=1200
请同学们思考两个问题:1.为什么会出现两个解?2.当a=1时C有几个解;当a= 时C有几个解;当a=3时C有几个解2019/3/13已知两边一对角解的分布表(如已知a,b,角A)2019/3/13四、反馈练习1、根据下列条件确定△ABC有两个解的是( )A.a=18 B=300 A=1200B.a=60 c=48 C=1200C.a=3 b=6 A=300D.a=14 b=15 A=4502、根据下列条件解三角形(1)已知在△ABC中a=8,B=600,C=450,求b(2)已知在△ABC中b= ,c=1,B=450, 求C由正弦定理可得:由正弦定理可得:答案:
1、由正弦定理可得:
A:
B:由于a>c,故A>C,无解
C:
D:2019/3/133、△ABC中,sinA
1、边的关系:2、角的关系:3、边角关系:1)两边之和大于第三边;两边之差小于第三边2)在直角三角形中:a2+b2=c21)A+B+C=18001)大边对大角,大角对大边,等边对等角2)在直角三角形ABC中,C=900,则回顾三角形中的边角关系:一、前提测评2019/3/131、知识目标
(1)使同学们理解正弦定理的推导过程
(2)能应用正弦定理解斜三角形
2、能力目标
培养同学们分析归纳的能力、分析问题解决问题的能力二、展示目标2019/3/13对任意三角形,这个等式都会成立吗?怎么证明这个结论?正弦定理的发现
2019/3/131、当?ABC为锐角三角形时,如图(1)证明:过A作单位向量 垂直,则 的夹角为________,
的夹角为________,
的夹角为________.已知:?ABC中,CB=a,AC=b,AB=c.
求证:方法一(向量法)(一)正弦定理的证明2019/3/132019/3/132、当?ABC为钝角三角形时,不妨设如图,同样可证得即等式对任意三角形都成立2019/3/13证法二:(等积法)在任意斜?ABC当中
作AD⊥BC于D ∴∵∴同理可证D2019/3/13证法三:(外接圆法)如图所示,作?ABC外接圆则∴同理D∠A=∠D2019/3/13正弦定理在任意一个三角形中,各边和它所对角的正弦的比相等,即注意:定理适合任意三角形。(2R是三角形外接圆的直径)2019/3/13正弦定理在解斜三角形中的两类应用:(1)、已知两角和任一边,求一角和其他两条边.(2)、已知两边和其中一边的对角,求另一边的对角(进而求其他的角和边)2019/3/13例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B 解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050 由 = 得 a= = =10由 =
得 b= = = 20sin750=20×
= 5 +5例题讲解:2019/3/13例2、在ΔABC中,b= ,B=600 ,c=1,求a和A,C 解:∵ = ∴ sinC= = =
∴ B=900 a= =2 ∵b>c,B=600 ∴C
b= = = +1∴C=600∴当C=600时,B=750 或C=12002019/3/13∴当C=1200 时,B=150 ,
b= = = -1
∴b= +1, B=750 ,C=600
或b= -1, B=150 ,C=1200
请同学们思考两个问题:1.为什么会出现两个解?2.当a=1时C有几个解;当a= 时C有几个解;当a=3时C有几个解2019/3/13已知两边一对角解的分布表(如已知a,b,角A)2019/3/13四、反馈练习1、根据下列条件确定△ABC有两个解的是( )A.a=18 B=300 A=1200B.a=60 c=48 C=1200C.a=3 b=6 A=300D.a=14 b=15 A=4502、根据下列条件解三角形(1)已知在△ABC中a=8,B=600,C=450,求b(2)已知在△ABC中b= ,c=1,B=450, 求C由正弦定理可得:由正弦定理可得:答案:
1、由正弦定理可得:
A:
B:由于a>c,故A>C,无解
C:
D:2019/3/133、△ABC中,sinA
