函数单调性(一)说课课件

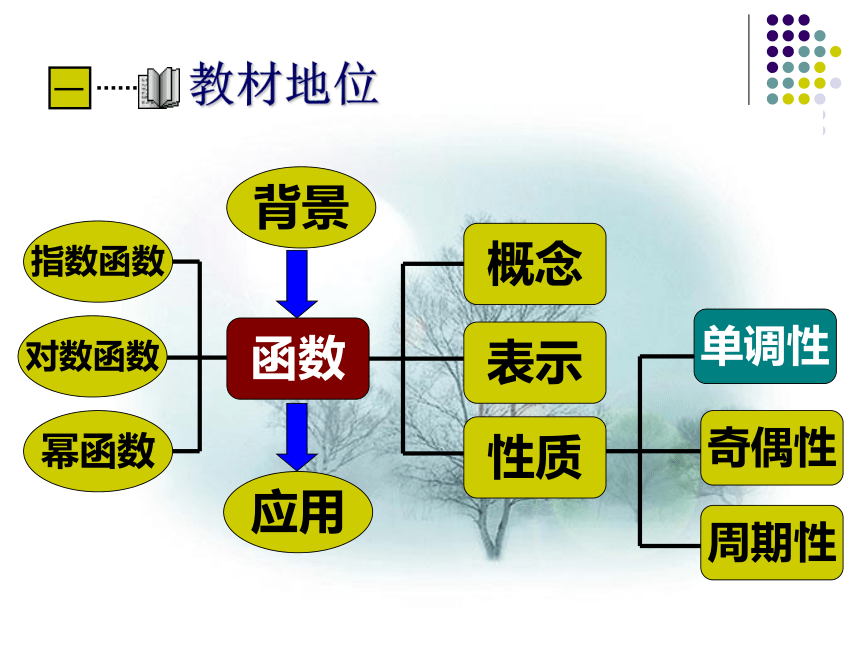
课件19张PPT。扬州大学附属中学 陆萍函数的单调性函数的单调性教材分析教法学法教学过程教学评价函数背景应用概念表示性质单调性奇偶性周期性指数函数对数函数幂函数教材地位教学目标知识与技能过程与方法情感态度与价值观　　使学生理解函数单调性
的概念，初步掌握判别函数
单调性的方法. 　　引导学生通过观察、归纳、抽象、概括，自主建构单调增函数、单调减函数等概念 ；能运用函数单调性概念解决简单的问题；让学生领会数形结合的数学思想方法 ，培养学生发现问题、分析问题 、解决问题的能力． 　　在函数单调性的学习过程中，
使学生体验数学的科学价值和应
用价值，培养学生善于观察、勇
于探索的良好习惯和严谨的科学
态度． 重点: 函数单调性的概念形成
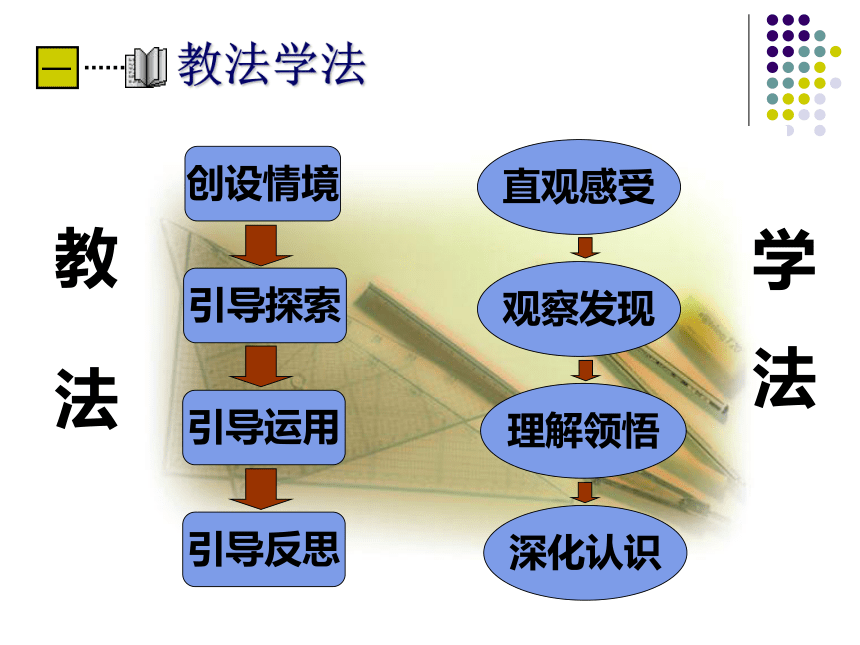
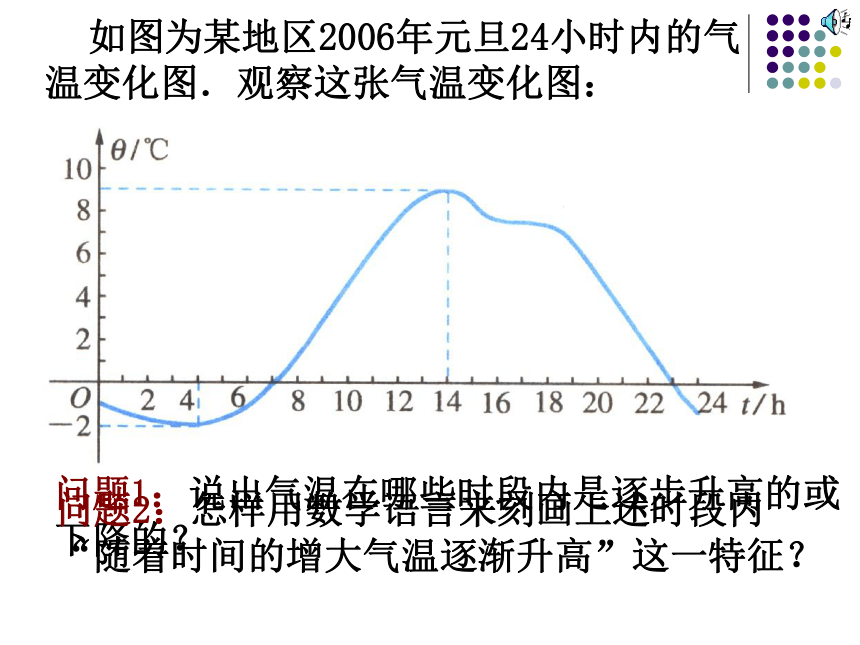
和初步运用； 难点: 函数单调性的概念形成． 教法学法引导探索引导运用引导反思创设情境直观感受观察发现理解领悟深化认识教 法学 法探究发现 建构概念创设情境 提出问题自我尝试 运用概念回顾反思 深化概念教学设计创设情境 提出问题 如图为某地区2006年元旦24小时内的气温变化图．观察这张气温变化图：问题1：说出气温在哪些时段内是逐步升高的或下降的？问题2：怎样用数学语言来刻画上述时段内“随着时间的增大气温逐渐升高”这一特征？探究发现 建构概念创设情境 提出问题自我尝试 运用概念回顾反思 深化概念教学设计 如图为某地区2006年元旦24小时内的气温变化图．观察这张气温变化图：问题1：说出气温在哪些时段内是逐步升高的或下降的？问题2：怎样用数学语言来刻画上述时段内“随着时间的增大气温逐渐升高”这一特征？t1t2f(t1)f(t2) 如图为某地区2006年元旦24小时内的气温变化图．观察这张气温变化图：问题3：对于任意的t1, t2∈[4,16]时，当t1< t2时，是否都有f(t1)有f(x1)＜f(x2)，那么就说y＝f(x)在区间I上是单调增函数， I称为y＝f(x)的单调增区间． 单调增函数区间I任意当x1＜x2时，都有f(x1)＜f(x2)问题4： 类比单调增函数概念，你能给出单调减函数的概念吗？ 探究发现 建构概念创设情境 提出问题自我尝试 运用概念回顾反思 深化概念教学设计单调增区间：单调减区间： [4，14][0，4]，[14，24]问题5：（1）你能找出气温图中的单调区间吗?运用xyOxyOxyO （2）你能说出你学过的函数的单调区间吗？请举例说明．运用问题6：证明 在区间（0，+ ∞）上是单调减函数． 探究发现 建构概念创设情境 提出问题自我尝试 运用概念回顾反思 深化概念教学设计2、若定义在R上的单调减函数 满足 ，试确定实数 的取值范围吗？1、定义在R上的单调函数 满足
，那么函数 是R上
的单调增函数还是单调减函数？
深化请思考下列问题:作业布置1、阅读课本P34－P35 例22、书面作业：
必做题：课本P43 1、4、7探究题：讨论函数 的单调性，并证
明你的结论. 教学评价参与程度合作意识思考习惯发现能力谢谢！