数学:1.2《应用举例》课件(新人教b版必修5)
文档属性
| 名称 | 数学:1.2《应用举例》课件(新人教b版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 299.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:10:00 | ||
图片预览

文档简介
课件13张PPT。2019/3/131.2应用举例 课件2019/3/13解应用题中的几个角的概念
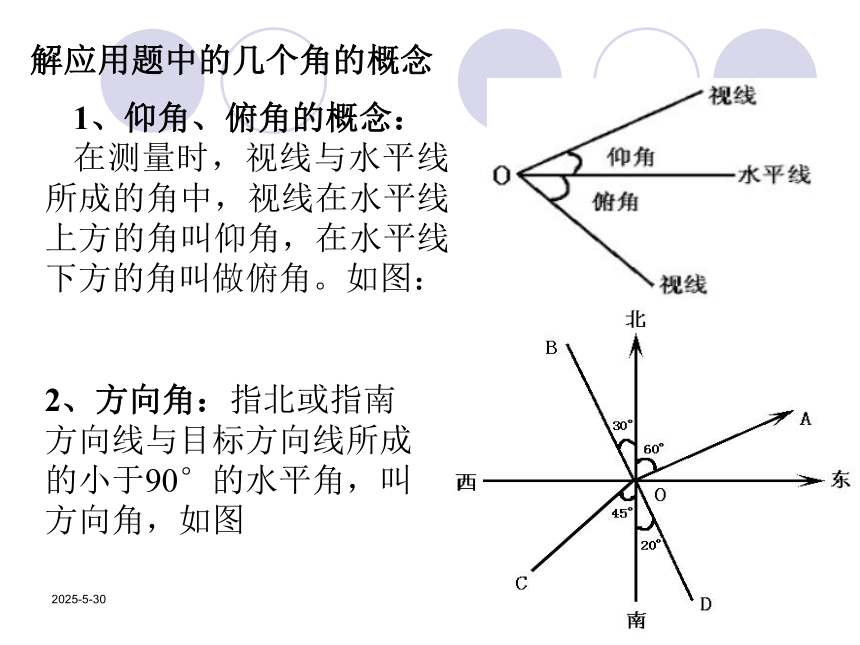
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 2019/3/13测量问题:1、水平距离的测量①两点间不能到达,
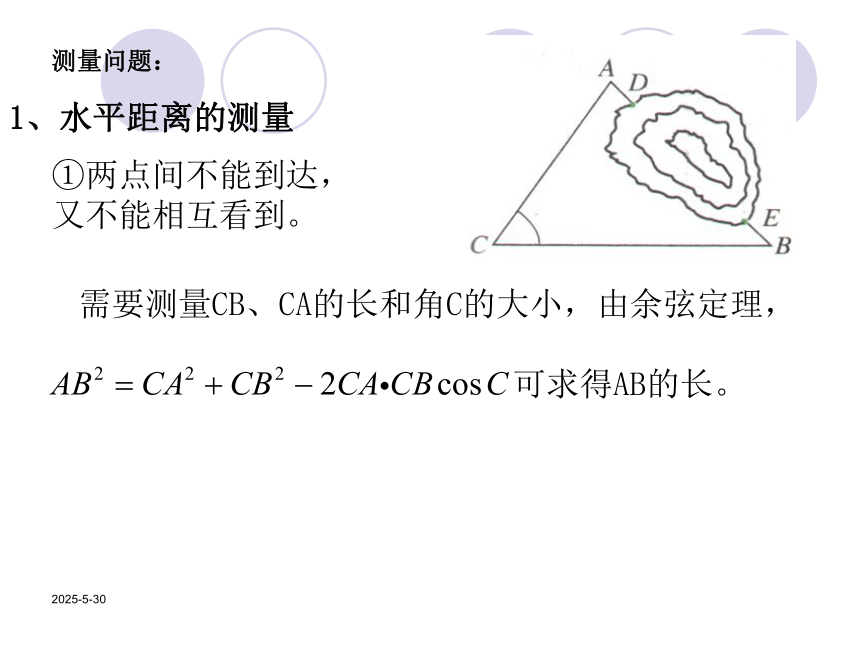
又不能相互看到。 需要测量CB、CA的长和角C的大小,由余弦定理,
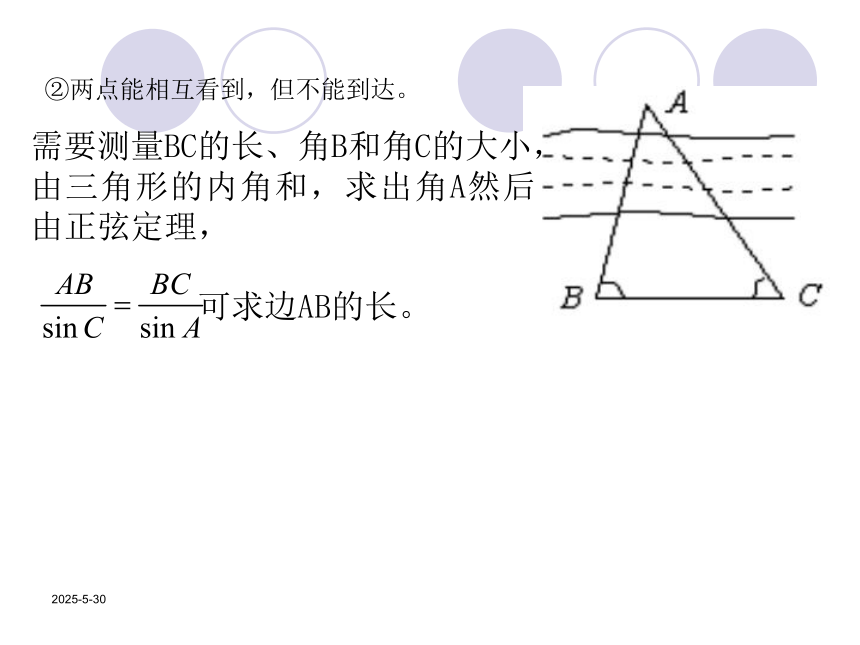
可求得AB的长。 2019/3/13②两点能相互看到,但不能到达。 需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
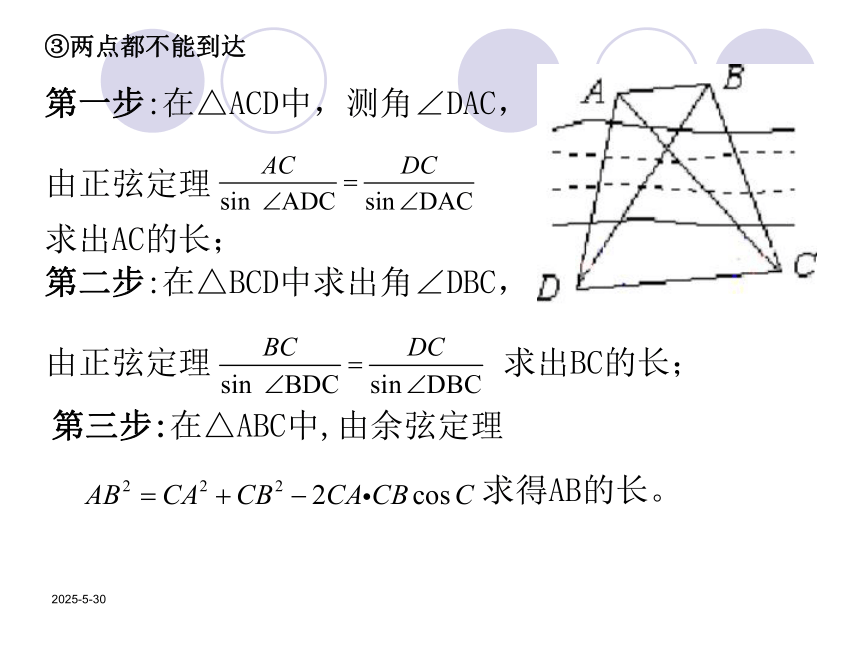
2019/3/13③两点都不能到达第一步:在△ACD中,测角∠DAC,
由正弦定理 求出AC的长; 第二步:在△BCD中求出角∠DBC,
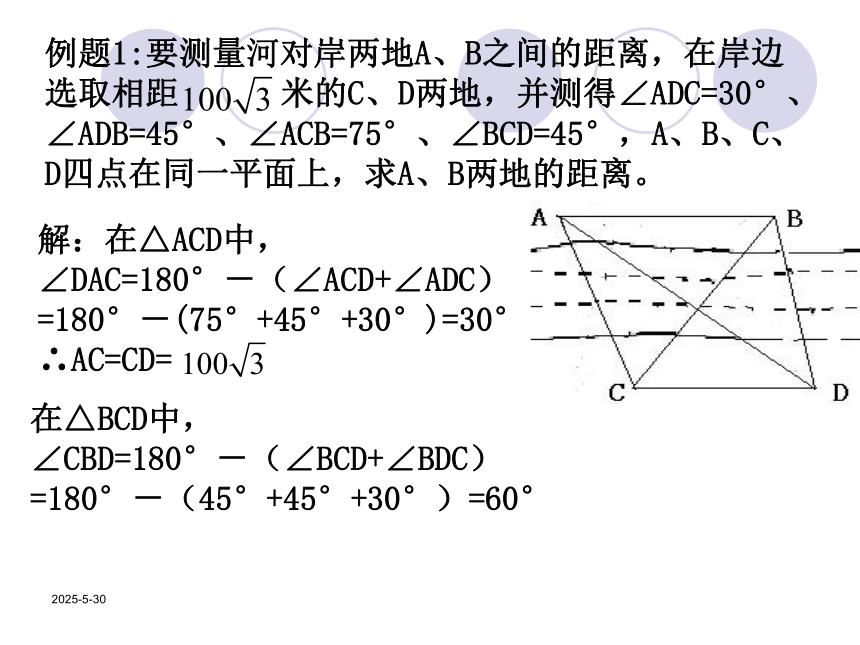
由正弦定理 求出BC的长; 第三步:在△ABC中,由余弦定理 求得AB的长。 2019/3/13例题1:要测量河对岸两地A、B之间的距离,在岸边选取相距 米的C、D两地,并测得∠ADC=30°、∠ADB=45°、∠ACB=75°、∠BCD=45°,A、B、C、D四点在同一平面上,求A、B两地的距离。 解:在△ACD中,
∠DAC=180°-(∠ACD+∠ADC)
=180°-(75°+45°+30°)=30°
∴AC=CD=
在△BCD中,
∠CBD=180°-(∠BCD+∠BDC)
=180°-(45°+45°+30°)=60° 2019/3/13由正弦定理 , 得在△ABC中由余弦定理, ∴所求A、B两地间的距离为 米。 2019/3/13测量垂直高度 1、底部可以到达的; 测量出角C和BC的长度,解直角三角形即可求出AB的长。 2、底部不能到达的 测量边CD,测量∠C和∠ADB, 2019/3/13
例题2:在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高 米,求山高 。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180°-(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32, 由正弦定理 ,
得 2019/3/13在等腰Rt△ACD中,故 ∴山的高度为 米。 2019/3/13例3 杆OA、OB所受的力(精确到0.1)。
2019/3/13例4如图在海滨某城市附近海面有一台风。据监测,台风中心位于城市A的南偏东300方向、距城市300km的海面P处,并以20km/h的速度向北偏西4500方向移动。如果台风侵袭的范围为圆形区域,半径为120km。问几小时后该城市开始受到台风的侵袭(精确到0.1h)?2019/3/131、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解解应用题的一般步骤是:
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 2019/3/13测量问题:1、水平距离的测量①两点间不能到达,
又不能相互看到。 需要测量CB、CA的长和角C的大小,由余弦定理,
可求得AB的长。 2019/3/13②两点能相互看到,但不能到达。 需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
2019/3/13③两点都不能到达第一步:在△ACD中,测角∠DAC,
由正弦定理 求出AC的长; 第二步:在△BCD中求出角∠DBC,
由正弦定理 求出BC的长; 第三步:在△ABC中,由余弦定理 求得AB的长。 2019/3/13例题1:要测量河对岸两地A、B之间的距离,在岸边选取相距 米的C、D两地,并测得∠ADC=30°、∠ADB=45°、∠ACB=75°、∠BCD=45°,A、B、C、D四点在同一平面上,求A、B两地的距离。 解:在△ACD中,
∠DAC=180°-(∠ACD+∠ADC)
=180°-(75°+45°+30°)=30°
∴AC=CD=
在△BCD中,
∠CBD=180°-(∠BCD+∠BDC)
=180°-(45°+45°+30°)=60° 2019/3/13由正弦定理 , 得在△ABC中由余弦定理, ∴所求A、B两地间的距离为 米。 2019/3/13测量垂直高度 1、底部可以到达的; 测量出角C和BC的长度,解直角三角形即可求出AB的长。 2、底部不能到达的 测量边CD,测量∠C和∠ADB, 2019/3/13
例题2:在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高 米,求山高 。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180°-(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32, 由正弦定理 ,
得 2019/3/13在等腰Rt△ACD中,故 ∴山的高度为 米。 2019/3/13例3 杆OA、OB所受的力(精确到0.1)。
2019/3/13例4如图在海滨某城市附近海面有一台风。据监测,台风中心位于城市A的南偏东300方向、距城市300km的海面P处,并以20km/h的速度向北偏西4500方向移动。如果台风侵袭的范围为圆形区域,半径为120km。问几小时后该城市开始受到台风的侵袭(精确到0.1h)?2019/3/131、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解解应用题的一般步骤是:
