2024年济南天桥区七年级下学期数学期中考试试卷(含答案)
文档属性
| 名称 | 2024年济南天桥区七年级下学期数学期中考试试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 19:13:06 | ||
图片预览


文档简介
2023-2024学年第二学期七年级期中考试(B)
数学试题(2024.05)
注意事项:
本试题共6页,满分为150分.考试时间为120分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用0.5mm黑色签字笔在答题卡上题号
所提示的答题区域作答,答案写在试卷上无效.
第I卷(选择题 共40分)
一.选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运算正确的是( )
A.a2·a4=a8 B.a4+a4=a8 C.(ab)3= a b3 D.(a2)4=a6
2.泉城广场鲜花盛放,数郁金香最为耀眼,某品种郁金香花粉直径约为0,000000032米,数据0.000000032用科学记数法表示为( )
A.0.32x10-7 B.3.2x10-8 C.3.2x10-7 D.32x10-9
3.研究表明,雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变
量是( )
A.雾霾的程度 B.城市中心 C.雾霾 D.城市中心区立体绿化面积
4.在下列四组线段中,能组成三角形的是( )
A.2,2,5 B.3,7,10 C.3,5,9 D.4,5,7
5.如图AB ∥CD,若∠1=40°,则∠2=( )
A.100° B.120° C.140° D.150°
(第5题图) (第6题图) (第9题图) (第10题图)
6.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列各式中,可以用平方差公式计算的是( )
A.(a-b)(a-b) B.(3a+2b)(3a-2b) C.(a+b)(2a-b) D.(2a+b)(-2a-b )
8.已知x2+mx+25是一个完全平方式,则m的值为( )
A.±5 B.10 C.﹣10 D.±10
9.如图:OB=OD,添加下列条件后不能保证△AOB≌△COD的是( )
A.OA=OC B.AB=CD C.∠A=∠C D.∠B=∠D
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分:②乙走完全程用了36分钟:③乙用16分钟追上甲:④乙到达终点时,甲离终点还有300米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题 共110分)
二.填空题(本大题共6个小题,每小题4分,共24分)
11.若一个角是38°,则这个角的余角为 .
12.4m2n÷(-2m)= .
13.在△ABC中,∠A:∠B:∠C=5:6:7,则△ABC是 (填入"锐鱼三角形"、"直角三角形"或"钝角三角形").
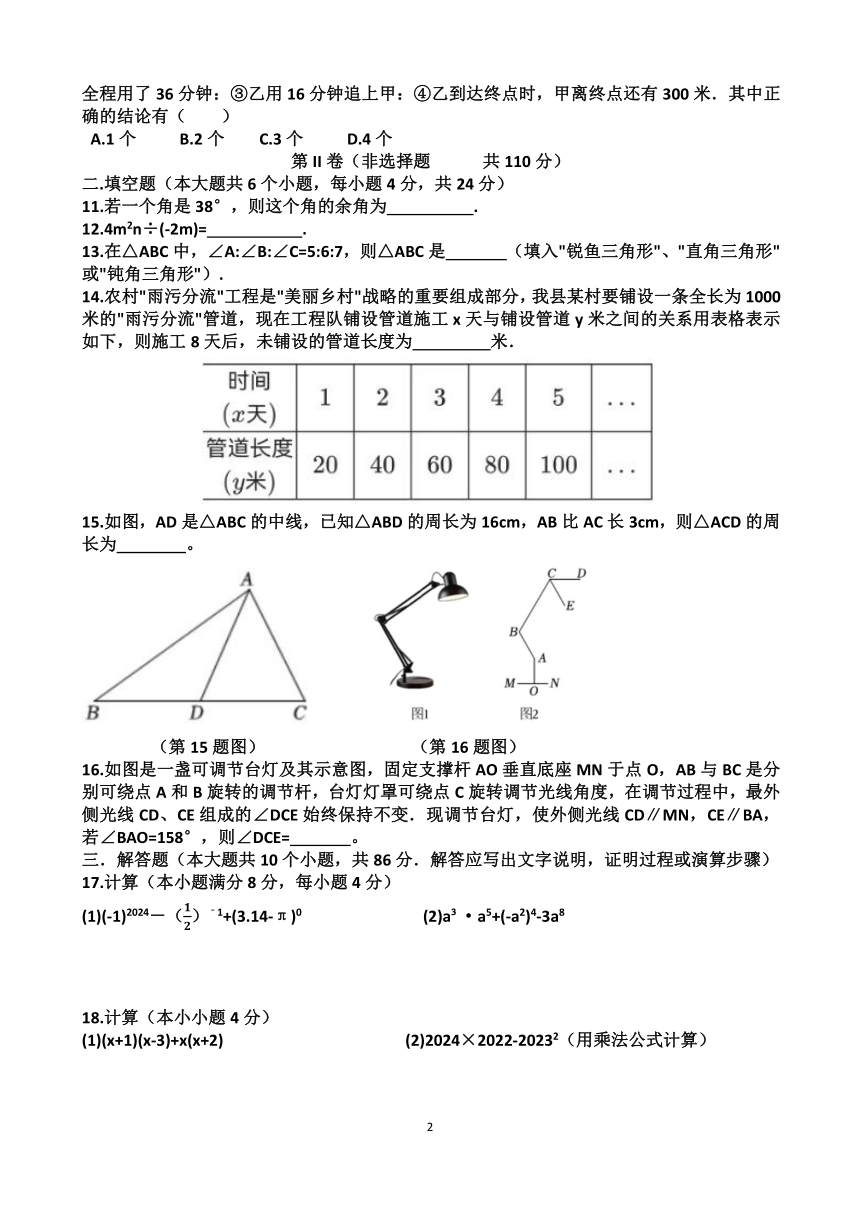
14.农村"雨污分流"工程是"美丽乡村"战略的重要组成部分,我县某村要铺设一条全长为1000米的"雨污分流"管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
15.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 。
(第15题图) (第16题图)
16.如图是一盏可调节台灯及其示意图,固定支撑杆AO垂直底座MN于点O,AB与BC是分别可绕点A和B旋转的调节杆,台灯灯罩可绕点C旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= 。
三.解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤)
17.计算(本小题满分8分,每小题4分)
(1)(-1)2024-()﹣1+(3.14-π)0 (2)a ·a5+(-a2)4-3a8
18.计算(本小小题4分)
(1)(x+1)(x-3)+x(x+2) (2)2024×2022-20232(用乘法公式计算)
19.先化简,后求值(本小题满分6分)
(x-2)2-(x-1)(x+1),其中x=2.
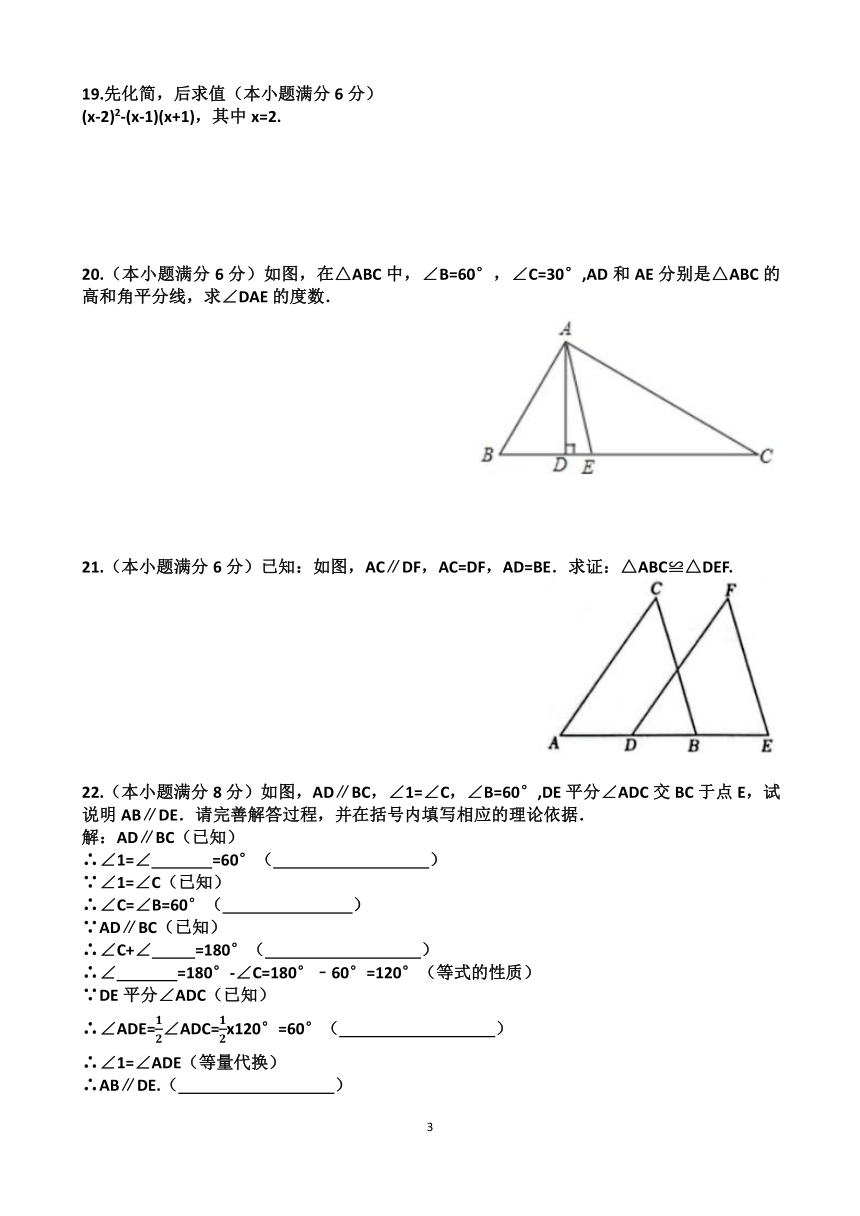
20.(本小题满分6分)如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
21.(本小题满分6分)已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
22.(本小题满分8分)如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:AD∥BC(已知)
∴∠1=∠ =60°( )
∵∠1=∠C(已知)
∴∠C=∠B=60°( )
∵AD∥BC(已知)
∴∠C+∠ =180°( )
∴∠ =180°-∠C=180°﹣60°=120°(等式的性质)
∵DE平分∠ADC(已知)
∴∠ADE=∠ADC=x120°=60°( )
∴∠1=∠ADE(等量代换)
∴AB∥DE.( )
23.(本小题满分10分)
观察下列等式:
(m-1)(m+1)=m2-1
(m-1)(m2+m+1)=m3-1
(m-1)(m +m2+m+1)= m4-1
(1)根据上面各式的规律,请写出第5个等式 .
(2)根据上面各式的规律可得(m-1)(mn+mn-1+……+m2+m+1)= (n为正整数,且n≥2).
(3)求22024+22023+…+22+2+1的值.
24.(本小题满分10分)下面是某项目化学习小组的部分学习过程再现,请阅读并解答问题.
【项目主题】品味经典.
【童话故事】"龟兔赛跑"讲述了这样的故事:兔子和乌龟从起点同时出发,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边小树处睡了一觉,当它醒来时,发现乌龟快到了终点了,于是急忙追赶,但为时已晚,乌龟先到达了终点
【分组探究】
A组成员用x表示兔子和乌龟从起点出发所行的时间,y1、y2分别表示兔子和乌龟所行的路程,画出了能大致表示上面故事情节的图象,如图1.
根据图1回答下列问题
问题1:赛跑的全程是 米,乌龟比兔子早到达终点 分钟;
问题2:乌龟在这次比赛中的平均速度是 米/分钟:
问题3:试解释图中线段AB的实际意义:
B组成员对童话故事进行了改编:兔子输了比赛,心里很不服气,它们约定再次赛跑,兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,乌龟、兔子的速度及赛场均和A组的数据一致,它们同时出发,结果兔子先到达了终点,小组成员根据故事情节绘制如图2的图象.
问题4:图2中,自变量x表示兔子和乌龟所行的时间,因变量y1、y2表示所行的路程,在乌龟行进过程中,当乌龟和兔子100米时,自变量x的是多少?
25.(本小题满分12分)将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题。如:a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab.
【阅读材料】
已知(3-x)(x-1)=-5,求(3-x)2+(x-1)2的值.
解:设3-x=a,x-1=b,则(3-x)(x-1)=ab=-5,a+b=3-x+x-1=2
∵a2+b2=(a+b)2-2ab
∴(3-x)2+(x-1)2=a2+b2=22-2×(-5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求 xy 的值;
(2)已知(4-x)(5-x)=8,(4-x)2+(5-x)2的值;
【问题解决】
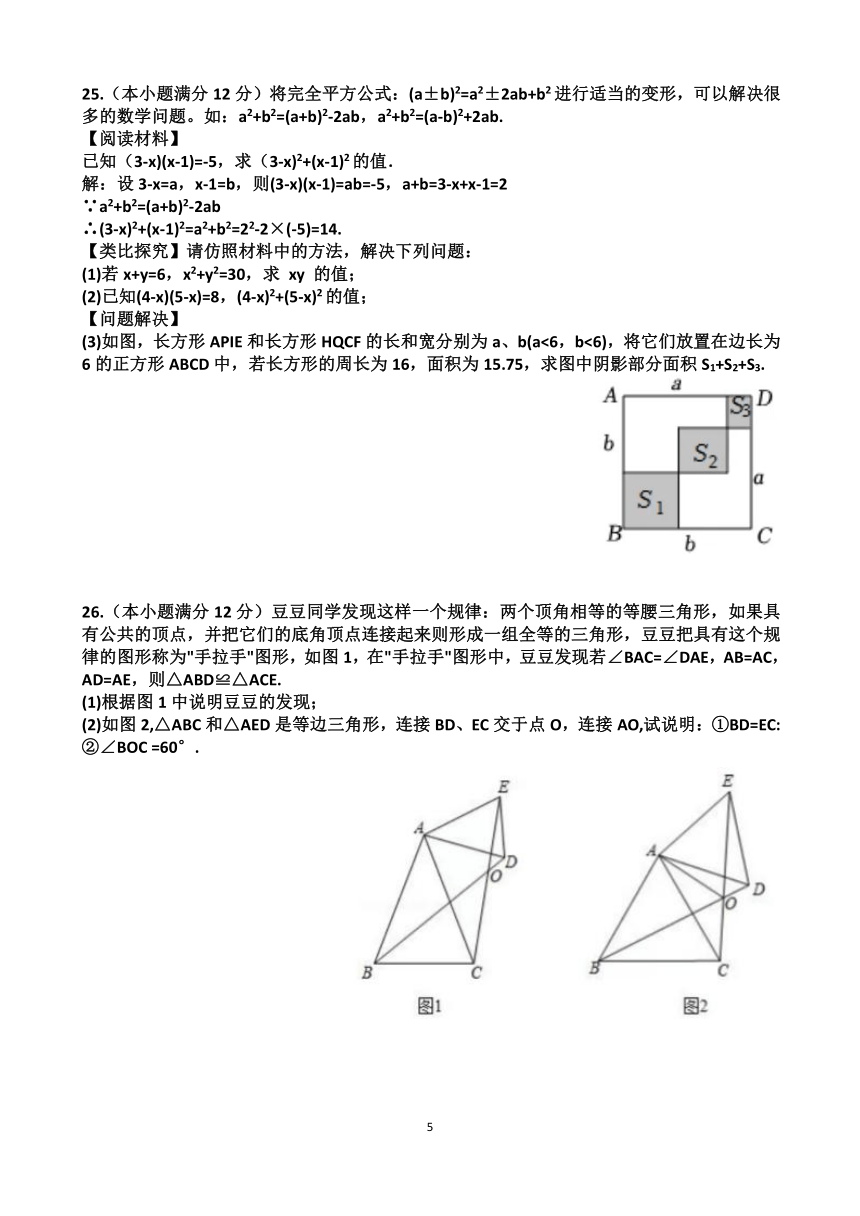
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a、b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
26.(本小题满分12分)豆豆同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,豆豆把具有这个规律的图形称为"手拉手"图形,如图1,在"手拉手"图形中,豆豆发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(1)根据图1中说明豆豆的发现;
(2)如图2,△ABC和△AED是等边三角形,连接BD、EC交于点O,连接AO,试说明:①BD=EC:②∠BOC =60°.
答案
一.选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运算正确的是( C )
A.a2·a4=a8 B.a4+a4=a8 C.(ab)3= a b3 D.(a2)4=a6
2.泉城广场鲜花盛放,数郁金香最为耀眼,某品种郁金香花粉直径约为0,000000032米,数据0.000000032用科学记数法表示为( B )
A.0.32x10-7 B.3.2x10-8 C.3.2x10-7 D.32x10-9
3.研究表明,雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变
量是( D )
A.雾霾的程度 B.城市中心 C.雾霾 D.城市中心区立体绿化面积
4.在下列四组线段中,能组成三角形的是( D )
A.2,2,5 B.3,7,10 C.3,5,9 D.4,5,7
5.如图AB ∥CD,若∠1=40°,则∠2=( C )
A.100° B.120° C.140° D.150°
(第5题图) (第6题图) (第9题图) (第10题图)
6.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( A )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列各式中,可以用平方差公式计算的是( B )
A.(a-b)(a-b) B.(3a+2b)(3a-2b) C.(a+b)(2a-b) D.(2a+b)(-2a-b )
8.已知x2+mx+25是一个完全平方式,则m的值为( D )
A.±5 B.10 C.﹣10 D.±10
9.如图:OB=OD,添加下列条件后不能保证△AOB≌△COD的是( B )
A.OA=OC B.AB=CD C.∠A=∠C D.∠B=∠D
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分:②乙走完全程用了36分钟:③乙用16分钟追上甲:④乙到达终点时,甲离终点还有300米.其中正确的结论有( A )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题 共110分)
二.填空题(本大题共6个小题,每小题4分,共24分)
11.若一个角是38°,则这个角的余角为 52° .
12.4m2n÷(-2m)= ﹣2mn .
13.在△ABC中,∠A:∠B:∠C=5:6:7,则△ABC是 锐角三角形 (填入"锐鱼三角形"、"直角三角形"或"钝角三角形").
14.农村"雨污分流"工程是"美丽乡村"战略的重要组成部分,我县某村要铺设一条全长为1000米的"雨污分流"管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 840 米.
15.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 13cm 。
(第15题图) (第16题图)
16.如图是一盏可调节台灯及其示意图,固定支撑杆AO垂直底座MN于点O,AB与BC是分别可绕点A和B旋转的调节杆,台灯灯罩可绕点C旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= 68° 。
三.解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤)
17.计算(本小题满分8分,每小题4分)
(1)(-1)2024-()﹣1+(3.14-π)0 (2)a ·a5+(-a2)4-3a8
=1-2+1 =a8+a8-3a8
=0 =﹣a8
18.计算(本小小题4分)
(1)(x+1)(x-3)+x(x+2) (2)2024×2022-20232(用乘法公式计算)
=x2-3x+x-3+x2+2x =(2023+1)(2023-1)-20232
=2x2-3 =﹣1
19.先化简,后求值(本小题满分6分)
(x-2)2-(x-1)(x+1),其中x=2.
解原式=x2-4x+4-x2+1
=﹣4x+5
将x=2代入得﹣4×2+5=﹣3
20.(本小题满分6分)如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
解:∵在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣30°=90°
∵AE是△ABC的角平分线
∴∠BAE=∠BAC
∵AD是△ABC的高,
∴∠ADB=90°
∴在△ADB中,∠BAD=90°﹣∠B=90°﹣60°=30°
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°
21.(本小题满分6分)已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
∵AC∥DF,
∴∠A=∠FDE
∵AD=BE,
∴AD+BD=BE+BD,即AB=DE
∵在△ABC和△DEF中,
∴△ABC≌△DEF(SAS)
22.(本小题满分8分)如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:AD∥BC(已知)
∴∠1=∠ B =60°( 两直线平行,同位角相等 )
∵∠1=∠C(已知)
∴∠C=∠B=60°( 等量代换 )
∵AD∥BC(已知)
∴∠C+∠ ADC =180°( 两直线平行,同旁内角互补 )
∴∠ ADC =180°-∠C=180°﹣60°=120°(等式的性质)
∵DE平分∠ADC(已知)
∴∠ADE=∠ADC=x120°=60°( 角平分线定义 )
∴∠1=∠ADE(等量代换)
∴AB∥DE.( 内错角相等,两直线平行 )
23.(本小题满分10分)
观察下列等式:
(m-1)(m+1)=m2-1
(m-1)(m2+m+1)=m3-1
(m-1)(m +m2+m+1)= m4-1
(1)根据上面各式的规律,请写出第5个等式 .
(2)根据上面各式的规律可得(m-1)(mn+mn-1+……+m2+m+1)= (n为正整数,且n≥2).
(3)求22024+22023+…+22+2+1的值.
(1)(m﹣1)(m5+m4+m3+m2+m+1)=m6﹣1
(2)mn+1﹣1
(3)∵(2﹣1)(22024+22023+…+22+2+1)=22025﹣1
∴22024+22023+…+22+2+1=22025﹣1
24.(本小题满分10分)下面是某项目化学习小组的部分学习过程再现,请阅读并解答问题.
【项目主题】品味经典.
【童话故事】"龟兔赛跑"讲述了这样的故事:兔子和乌龟从起点同时出发,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边小树处睡了一觉,当它醒来时,发现乌龟快到了终点了,于是急忙追赶,但为时已晚,乌龟先到达了终点
【分组探究】
A组成员用x表示兔子和乌龟从起点出发所行的时间,y1、y2分别表示兔子和乌龟所行的路程,画出了能大致表示上面故事情节的图象,如图1.
根据图1回答下列问题
问题1:赛跑的全程是 米,乌龟比兔子早到达终点 分钟;
问题2:乌龟在这次比赛中的平均速度是 米/分钟:
问题3:试解释图中线段AB的实际意义:
B组成员对童话故事进行了改编:兔子输了比赛,心里很不服气,它们约定再次赛跑,兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,乌龟、兔子的速度及赛场均和A组的数据一致,它们同时出发,结果兔子先到达了终点,小组成员根据故事情节绘制如图2的图象.
问题4:图2中,自变量x表示兔子和乌龟所行的时间,因变量y1、y2表示所行的路程,在乌龟行进过程中,当乌龟和兔子100米时,自变量x的是多少?
问题1:赛跑的全程是1200米,乌龟比兔子早到达终点10分钟;
问题2:乌龟在这次比赛中的平均速度是20米/分钟;
问题3:线段AB表示兔子在路边小树处睡觉;
问题4:
解:兔子的速度:v=1200÷30=40(米/分钟)
①兔子未追上乌龟时
40x-20x=400-100
解得x=15
②兔子追上乌龟后,未到达终点前
40x-20x=400+100
解得x=25
③兔子到达终点后
40-(100÷20) =35
综上所述,在乌龟行进过程中,当乌龟和兔子相距100米时,自变量x的值是15,25或35.
25.(本小题满分12分)将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题。如:a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab.
【阅读材料】
已知(3-x)(x-1)=-5,求(3-x)2+(x-1)2的值.
解:设3-x=a,x-1=b,则(3-x)(x-1)=ab=-5,a+b=3-x+x-1=2
∵a2+b2=(a+b)2-2ab
∴(3-x)2+(x-1)2=a2+b2=22-2×(-5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求 xy 的值;
(2)已知(4-x)(5-x)=8,(4-x)2+(5-x)2的值;
【问题解决】
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a、b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
解:(1)∵(x+y)2=x2+y2+2xy,x+y=6,x2+y2=30
∴62=30+2xy
解得xy=3
(2)设4﹣x=a,5﹣x=b,
则(4﹣x)(5﹣x)=ab=8,a﹣b=(4﹣x)﹣(5﹣x)=﹣1
∵(a﹣b)2=a2+b2﹣2ab
∴(﹣1)2=a2+b2﹣2×8
∴a2+b2=17,
∴(4﹣x)2+(5﹣x)2=17
(3)∵长方形的周长为16,面积为15.75,
∴a+b=8,ab=15.75
如图,得到ED=6﹣a,HG=b﹣(6﹣a)=a+b﹣6=8﹣6=2,BQ=6﹣b
∴S1+S2+S3=(6﹣b)2+22+(6﹣a)2
=72﹣12(a+b)+4+a2+b2
=72﹣12×8+4+(a+b)2﹣2ab
=72﹣12×8+4+82﹣2×15.75
=12.5
26.(本小题满分12分)豆豆同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,豆豆把具有这个规律的图形称为"手拉手"图形,如图1,在"手拉手"图形中,豆豆发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(1)根据图1中说明豆豆的发现;
(2)如图2,△ABC和△AED是等边三角形,连接BD、EC交于点O,连接AO,试说明:①BD=EC:②∠BOC =60°.
证明:(1)∵∠BAC=∠DAE
∴∠BAC+∠CAD=∠DAE+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
(2)①如图2
∵△ABC和△ADE是等边三角形
∴AB=AC,AD=AE,∠BAC=∠DAE=60°
∴∠BAC+∠CAD=∠DAE+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴BD=EC
②∵△ABC是等边三角形
∴∠ABC=∠ACB=60°
∵△ABD≌△ACE
∴∠ABD=∠ACE
∴∠BOC=180°﹣∠OBC﹣∠OCA﹣∠ACB
=180°﹣∠OBC﹣∠ABD﹣∠ACB
=180°﹣60°﹣60°
=60°
数学试题(2024.05)
注意事项:
本试题共6页,满分为150分.考试时间为120分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用0.5mm黑色签字笔在答题卡上题号
所提示的答题区域作答,答案写在试卷上无效.
第I卷(选择题 共40分)
一.选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运算正确的是( )
A.a2·a4=a8 B.a4+a4=a8 C.(ab)3= a b3 D.(a2)4=a6
2.泉城广场鲜花盛放,数郁金香最为耀眼,某品种郁金香花粉直径约为0,000000032米,数据0.000000032用科学记数法表示为( )
A.0.32x10-7 B.3.2x10-8 C.3.2x10-7 D.32x10-9
3.研究表明,雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变
量是( )
A.雾霾的程度 B.城市中心 C.雾霾 D.城市中心区立体绿化面积
4.在下列四组线段中,能组成三角形的是( )
A.2,2,5 B.3,7,10 C.3,5,9 D.4,5,7
5.如图AB ∥CD,若∠1=40°,则∠2=( )
A.100° B.120° C.140° D.150°
(第5题图) (第6题图) (第9题图) (第10题图)
6.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列各式中,可以用平方差公式计算的是( )
A.(a-b)(a-b) B.(3a+2b)(3a-2b) C.(a+b)(2a-b) D.(2a+b)(-2a-b )
8.已知x2+mx+25是一个完全平方式,则m的值为( )
A.±5 B.10 C.﹣10 D.±10
9.如图:OB=OD,添加下列条件后不能保证△AOB≌△COD的是( )
A.OA=OC B.AB=CD C.∠A=∠C D.∠B=∠D
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分:②乙走完全程用了36分钟:③乙用16分钟追上甲:④乙到达终点时,甲离终点还有300米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题 共110分)
二.填空题(本大题共6个小题,每小题4分,共24分)
11.若一个角是38°,则这个角的余角为 .
12.4m2n÷(-2m)= .
13.在△ABC中,∠A:∠B:∠C=5:6:7,则△ABC是 (填入"锐鱼三角形"、"直角三角形"或"钝角三角形").
14.农村"雨污分流"工程是"美丽乡村"战略的重要组成部分,我县某村要铺设一条全长为1000米的"雨污分流"管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
15.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 。
(第15题图) (第16题图)
16.如图是一盏可调节台灯及其示意图,固定支撑杆AO垂直底座MN于点O,AB与BC是分别可绕点A和B旋转的调节杆,台灯灯罩可绕点C旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= 。
三.解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤)
17.计算(本小题满分8分,每小题4分)
(1)(-1)2024-()﹣1+(3.14-π)0 (2)a ·a5+(-a2)4-3a8
18.计算(本小小题4分)
(1)(x+1)(x-3)+x(x+2) (2)2024×2022-20232(用乘法公式计算)
19.先化简,后求值(本小题满分6分)
(x-2)2-(x-1)(x+1),其中x=2.
20.(本小题满分6分)如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
21.(本小题满分6分)已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
22.(本小题满分8分)如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:AD∥BC(已知)
∴∠1=∠ =60°( )
∵∠1=∠C(已知)
∴∠C=∠B=60°( )
∵AD∥BC(已知)
∴∠C+∠ =180°( )
∴∠ =180°-∠C=180°﹣60°=120°(等式的性质)
∵DE平分∠ADC(已知)
∴∠ADE=∠ADC=x120°=60°( )
∴∠1=∠ADE(等量代换)
∴AB∥DE.( )
23.(本小题满分10分)
观察下列等式:
(m-1)(m+1)=m2-1
(m-1)(m2+m+1)=m3-1
(m-1)(m +m2+m+1)= m4-1
(1)根据上面各式的规律,请写出第5个等式 .
(2)根据上面各式的规律可得(m-1)(mn+mn-1+……+m2+m+1)= (n为正整数,且n≥2).
(3)求22024+22023+…+22+2+1的值.
24.(本小题满分10分)下面是某项目化学习小组的部分学习过程再现,请阅读并解答问题.
【项目主题】品味经典.
【童话故事】"龟兔赛跑"讲述了这样的故事:兔子和乌龟从起点同时出发,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边小树处睡了一觉,当它醒来时,发现乌龟快到了终点了,于是急忙追赶,但为时已晚,乌龟先到达了终点
【分组探究】
A组成员用x表示兔子和乌龟从起点出发所行的时间,y1、y2分别表示兔子和乌龟所行的路程,画出了能大致表示上面故事情节的图象,如图1.
根据图1回答下列问题
问题1:赛跑的全程是 米,乌龟比兔子早到达终点 分钟;
问题2:乌龟在这次比赛中的平均速度是 米/分钟:
问题3:试解释图中线段AB的实际意义:
B组成员对童话故事进行了改编:兔子输了比赛,心里很不服气,它们约定再次赛跑,兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,乌龟、兔子的速度及赛场均和A组的数据一致,它们同时出发,结果兔子先到达了终点,小组成员根据故事情节绘制如图2的图象.
问题4:图2中,自变量x表示兔子和乌龟所行的时间,因变量y1、y2表示所行的路程,在乌龟行进过程中,当乌龟和兔子100米时,自变量x的是多少?
25.(本小题满分12分)将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题。如:a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab.
【阅读材料】
已知(3-x)(x-1)=-5,求(3-x)2+(x-1)2的值.
解:设3-x=a,x-1=b,则(3-x)(x-1)=ab=-5,a+b=3-x+x-1=2
∵a2+b2=(a+b)2-2ab
∴(3-x)2+(x-1)2=a2+b2=22-2×(-5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求 xy 的值;
(2)已知(4-x)(5-x)=8,(4-x)2+(5-x)2的值;
【问题解决】
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a、b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
26.(本小题满分12分)豆豆同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,豆豆把具有这个规律的图形称为"手拉手"图形,如图1,在"手拉手"图形中,豆豆发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(1)根据图1中说明豆豆的发现;
(2)如图2,△ABC和△AED是等边三角形,连接BD、EC交于点O,连接AO,试说明:①BD=EC:②∠BOC =60°.
答案
一.选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运算正确的是( C )
A.a2·a4=a8 B.a4+a4=a8 C.(ab)3= a b3 D.(a2)4=a6
2.泉城广场鲜花盛放,数郁金香最为耀眼,某品种郁金香花粉直径约为0,000000032米,数据0.000000032用科学记数法表示为( B )
A.0.32x10-7 B.3.2x10-8 C.3.2x10-7 D.32x10-9
3.研究表明,雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变
量是( D )
A.雾霾的程度 B.城市中心 C.雾霾 D.城市中心区立体绿化面积
4.在下列四组线段中,能组成三角形的是( D )
A.2,2,5 B.3,7,10 C.3,5,9 D.4,5,7
5.如图AB ∥CD,若∠1=40°,则∠2=( C )
A.100° B.120° C.140° D.150°
(第5题图) (第6题图) (第9题图) (第10题图)
6.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( A )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列各式中,可以用平方差公式计算的是( B )
A.(a-b)(a-b) B.(3a+2b)(3a-2b) C.(a+b)(2a-b) D.(2a+b)(-2a-b )
8.已知x2+mx+25是一个完全平方式,则m的值为( D )
A.±5 B.10 C.﹣10 D.±10
9.如图:OB=OD,添加下列条件后不能保证△AOB≌△COD的是( B )
A.OA=OC B.AB=CD C.∠A=∠C D.∠B=∠D
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分:②乙走完全程用了36分钟:③乙用16分钟追上甲:④乙到达终点时,甲离终点还有300米.其中正确的结论有( A )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题 共110分)
二.填空题(本大题共6个小题,每小题4分,共24分)
11.若一个角是38°,则这个角的余角为 52° .
12.4m2n÷(-2m)= ﹣2mn .
13.在△ABC中,∠A:∠B:∠C=5:6:7,则△ABC是 锐角三角形 (填入"锐鱼三角形"、"直角三角形"或"钝角三角形").
14.农村"雨污分流"工程是"美丽乡村"战略的重要组成部分,我县某村要铺设一条全长为1000米的"雨污分流"管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 840 米.
15.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 13cm 。
(第15题图) (第16题图)
16.如图是一盏可调节台灯及其示意图,固定支撑杆AO垂直底座MN于点O,AB与BC是分别可绕点A和B旋转的调节杆,台灯灯罩可绕点C旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= 68° 。
三.解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤)
17.计算(本小题满分8分,每小题4分)
(1)(-1)2024-()﹣1+(3.14-π)0 (2)a ·a5+(-a2)4-3a8
=1-2+1 =a8+a8-3a8
=0 =﹣a8
18.计算(本小小题4分)
(1)(x+1)(x-3)+x(x+2) (2)2024×2022-20232(用乘法公式计算)
=x2-3x+x-3+x2+2x =(2023+1)(2023-1)-20232
=2x2-3 =﹣1
19.先化简,后求值(本小题满分6分)
(x-2)2-(x-1)(x+1),其中x=2.
解原式=x2-4x+4-x2+1
=﹣4x+5
将x=2代入得﹣4×2+5=﹣3
20.(本小题满分6分)如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
解:∵在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣30°=90°
∵AE是△ABC的角平分线
∴∠BAE=∠BAC
∵AD是△ABC的高,
∴∠ADB=90°
∴在△ADB中,∠BAD=90°﹣∠B=90°﹣60°=30°
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°
21.(本小题满分6分)已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
∵AC∥DF,
∴∠A=∠FDE
∵AD=BE,
∴AD+BD=BE+BD,即AB=DE
∵在△ABC和△DEF中,
∴△ABC≌△DEF(SAS)
22.(本小题满分8分)如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:AD∥BC(已知)
∴∠1=∠ B =60°( 两直线平行,同位角相等 )
∵∠1=∠C(已知)
∴∠C=∠B=60°( 等量代换 )
∵AD∥BC(已知)
∴∠C+∠ ADC =180°( 两直线平行,同旁内角互补 )
∴∠ ADC =180°-∠C=180°﹣60°=120°(等式的性质)
∵DE平分∠ADC(已知)
∴∠ADE=∠ADC=x120°=60°( 角平分线定义 )
∴∠1=∠ADE(等量代换)
∴AB∥DE.( 内错角相等,两直线平行 )
23.(本小题满分10分)
观察下列等式:
(m-1)(m+1)=m2-1
(m-1)(m2+m+1)=m3-1
(m-1)(m +m2+m+1)= m4-1
(1)根据上面各式的规律,请写出第5个等式 .
(2)根据上面各式的规律可得(m-1)(mn+mn-1+……+m2+m+1)= (n为正整数,且n≥2).
(3)求22024+22023+…+22+2+1的值.
(1)(m﹣1)(m5+m4+m3+m2+m+1)=m6﹣1
(2)mn+1﹣1
(3)∵(2﹣1)(22024+22023+…+22+2+1)=22025﹣1
∴22024+22023+…+22+2+1=22025﹣1
24.(本小题满分10分)下面是某项目化学习小组的部分学习过程再现,请阅读并解答问题.
【项目主题】品味经典.
【童话故事】"龟兔赛跑"讲述了这样的故事:兔子和乌龟从起点同时出发,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边小树处睡了一觉,当它醒来时,发现乌龟快到了终点了,于是急忙追赶,但为时已晚,乌龟先到达了终点
【分组探究】
A组成员用x表示兔子和乌龟从起点出发所行的时间,y1、y2分别表示兔子和乌龟所行的路程,画出了能大致表示上面故事情节的图象,如图1.
根据图1回答下列问题
问题1:赛跑的全程是 米,乌龟比兔子早到达终点 分钟;
问题2:乌龟在这次比赛中的平均速度是 米/分钟:
问题3:试解释图中线段AB的实际意义:
B组成员对童话故事进行了改编:兔子输了比赛,心里很不服气,它们约定再次赛跑,兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,乌龟、兔子的速度及赛场均和A组的数据一致,它们同时出发,结果兔子先到达了终点,小组成员根据故事情节绘制如图2的图象.
问题4:图2中,自变量x表示兔子和乌龟所行的时间,因变量y1、y2表示所行的路程,在乌龟行进过程中,当乌龟和兔子100米时,自变量x的是多少?
问题1:赛跑的全程是1200米,乌龟比兔子早到达终点10分钟;
问题2:乌龟在这次比赛中的平均速度是20米/分钟;
问题3:线段AB表示兔子在路边小树处睡觉;
问题4:
解:兔子的速度:v=1200÷30=40(米/分钟)
①兔子未追上乌龟时
40x-20x=400-100
解得x=15
②兔子追上乌龟后,未到达终点前
40x-20x=400+100
解得x=25
③兔子到达终点后
40-(100÷20) =35
综上所述,在乌龟行进过程中,当乌龟和兔子相距100米时,自变量x的值是15,25或35.
25.(本小题满分12分)将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题。如:a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab.
【阅读材料】
已知(3-x)(x-1)=-5,求(3-x)2+(x-1)2的值.
解:设3-x=a,x-1=b,则(3-x)(x-1)=ab=-5,a+b=3-x+x-1=2
∵a2+b2=(a+b)2-2ab
∴(3-x)2+(x-1)2=a2+b2=22-2×(-5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求 xy 的值;
(2)已知(4-x)(5-x)=8,(4-x)2+(5-x)2的值;
【问题解决】
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a、b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
解:(1)∵(x+y)2=x2+y2+2xy,x+y=6,x2+y2=30
∴62=30+2xy
解得xy=3
(2)设4﹣x=a,5﹣x=b,
则(4﹣x)(5﹣x)=ab=8,a﹣b=(4﹣x)﹣(5﹣x)=﹣1
∵(a﹣b)2=a2+b2﹣2ab
∴(﹣1)2=a2+b2﹣2×8
∴a2+b2=17,
∴(4﹣x)2+(5﹣x)2=17
(3)∵长方形的周长为16,面积为15.75,
∴a+b=8,ab=15.75
如图,得到ED=6﹣a,HG=b﹣(6﹣a)=a+b﹣6=8﹣6=2,BQ=6﹣b
∴S1+S2+S3=(6﹣b)2+22+(6﹣a)2
=72﹣12(a+b)+4+a2+b2
=72﹣12×8+4+(a+b)2﹣2ab
=72﹣12×8+4+82﹣2×15.75
=12.5
26.(本小题满分12分)豆豆同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,豆豆把具有这个规律的图形称为"手拉手"图形,如图1,在"手拉手"图形中,豆豆发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(1)根据图1中说明豆豆的发现;
(2)如图2,△ABC和△AED是等边三角形,连接BD、EC交于点O,连接AO,试说明:①BD=EC:②∠BOC =60°.
证明:(1)∵∠BAC=∠DAE
∴∠BAC+∠CAD=∠DAE+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
(2)①如图2
∵△ABC和△ADE是等边三角形
∴AB=AC,AD=AE,∠BAC=∠DAE=60°
∴∠BAC+∠CAD=∠DAE+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴BD=EC
②∵△ABC是等边三角形
∴∠ABC=∠ACB=60°
∵△ABD≌△ACE
∴∠ABD=∠ACE
∴∠BOC=180°﹣∠OBC﹣∠OCA﹣∠ACB
=180°﹣∠OBC﹣∠ABD﹣∠ACB
=180°﹣60°﹣60°
=60°
同课章节目录
