数学:1.3.4《三角函数中的最值问题》课件(苏教版必修4)
文档属性
| 名称 | 数学:1.3.4《三角函数中的最值问题》课件(苏教版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:10:00 | ||
图片预览





文档简介
课件19张PPT。2019/3/13三角函数复习课 三角函数的最值问题
新沂市第一中学 高三数学组 授课人: 安勇2019/3/13重点:让学生能运用三角函数概念、图象、性质、同角三角函数的基本关系式、和差角公式等求有关最值问题;掌握求最值常见思想方法。
难点:利用三角函数的性质求有关最值。下页2019/3/13一)复习回顾 2.y=sinx,y=cosx的值域是———— 。
3.y=asinx+bcosx的值域是———— 。
4.a+b=m,求a b 的最大值? (a>0,b>0,m>0)5.函数f(x)在[a,b]上单调递增,则f(x)的最小值为———— ,最大值为———— 。f(a)f(b)[-1,1][- , ]1、求函数最值常见方法:利用基本函数法,配方法,分离常数法,换元法,数形结合法,基本不等式法,函数单调性法等等2019/3/131、求下列函数的 (-1≤x≤ 1)最大
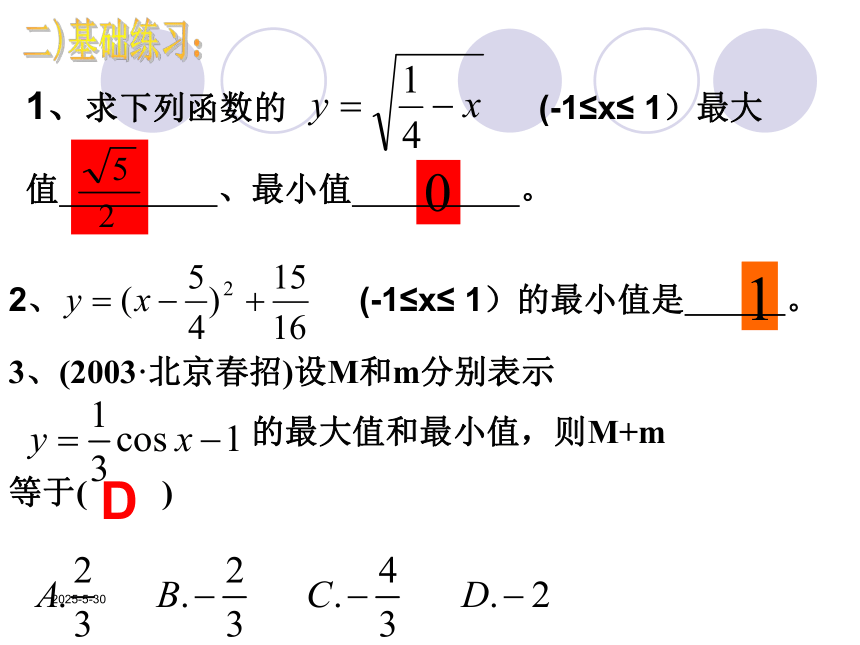
值 、最小值 。
二)基础练习:2、 (-1≤x≤ 1)的最小值是 。3、(2003·北京春招)设M和m分别表示
的最大值和最小值,则M+m
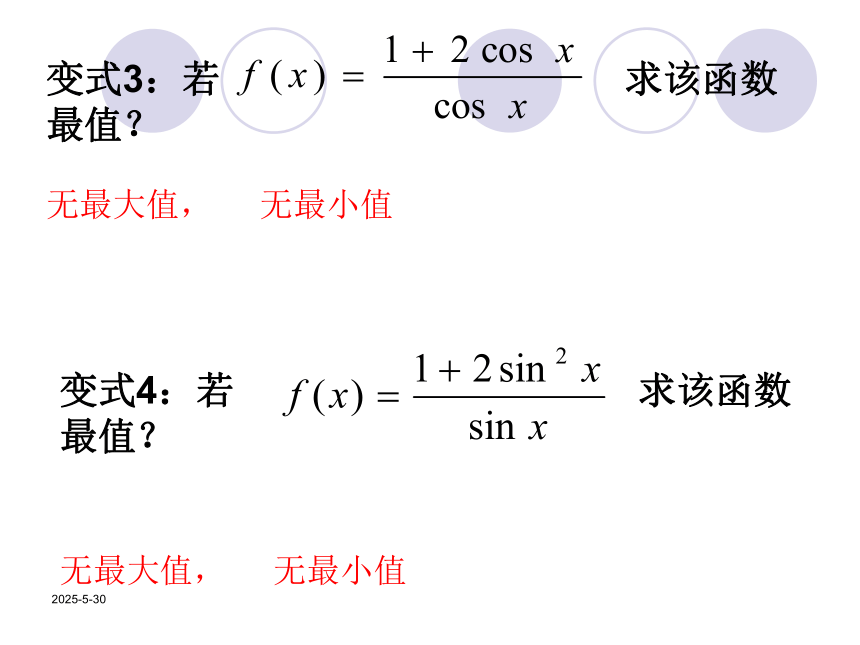
等于( )D2019/3/13三)典型应用【例1】已知函数y=3cosx-2,求该函数的最值?变式1:若x ?变式2:y= 求y的最值? 最大值为 1 最小值为-5最大值为 1 , 最小值为无最大值, 无最小值2019/3/13变式3:若 求该函数最值? 变式4:若 求该函数最值?无最大值, 无最小值无最大值, 无最小值2019/3/13变式5:
已知函数f(x)=cos4x–2sinxcosx–sin4x,
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若x∈[0, ],求f(x)的最大值、最小值.解析:(Ⅰ)因为 与例1有何关系?2019/3/132019/3/13【例2】已知 函数y=2sinx+3cosx ,求该函数的最值?变式1:一般地y=a sinx+b cosx,其中a、b 为已知实数,a、b为任意实数,求其最值?最大值为 最小值为-最大值为 最小值为-2019/3/13【例3】 已知 ,求该函数的最值? 变式1:已知
求该函数的最值?变式练习:已知
求该函数的最值? 最大值为 最小值为最大值为 5 最小值为12019/3/13典型例题【例4】 已知函数
求该函数最值?
法一)解析:(法一):函数
的几何意义为两点 连线的斜率k,而Q点的轨迹为单位圆,则有:
2019/3/13 (法二): 2019/3/13变式1:已知函数
求函数的最值?最大值为 , 最小值为2019/3/131、已知 ,则( )
A、函数最小值为–2,最大值为0
B、函数的最小值为–4
C、函数无最小值,最大值为0
D、函数最小值为–4,最大值为4 C2、已知, 求函数的最小值是 。
四)巩固测试小试身手2019/3/133.已知 求
的最值?4.求 的最值?5.设x、y满足x2 + y2 =1,求 3x+4y 的最大值? 最大值为 1, 最小值0最大值为5最大值为 最小值为2019/3/13课外作业:1、函数y=(sinx+1)(cosx+1)的最大值和最小值
分别是 、 .2019/3/132、设函数y=acosx+b(a,b为常数且a>0)的最大值为1,最小值为–7,那么acosx+bsinx的最大值为 ( )
A、3 B、4 C、5 D、63、设函数y=4sinx cosx+sin2x+1,求y的最值?2019/3/13五、课堂小结1、化为一个角的三角函数,再利用有界性求最值 2?、配方法求最值:转化为二次函数在闭区间上
的最值问题,一、 如求函数 二、如 同时出现的题型。
用换元法解决 5、换元法求最值尤其是三角换元3、分离常数法,解决形如 型的函数。4、数形结合,解决形如 型的函数。6、利用不等式单调性求最值2019/3/13六)作业: P69 T8-T11-T12
新沂市第一中学 高三数学组 授课人: 安勇2019/3/13重点:让学生能运用三角函数概念、图象、性质、同角三角函数的基本关系式、和差角公式等求有关最值问题;掌握求最值常见思想方法。
难点:利用三角函数的性质求有关最值。下页2019/3/13一)复习回顾 2.y=sinx,y=cosx的值域是———— 。
3.y=asinx+bcosx的值域是———— 。
4.a+b=m,求a b 的最大值? (a>0,b>0,m>0)5.函数f(x)在[a,b]上单调递增,则f(x)的最小值为———— ,最大值为———— 。f(a)f(b)[-1,1][- , ]1、求函数最值常见方法:利用基本函数法,配方法,分离常数法,换元法,数形结合法,基本不等式法,函数单调性法等等2019/3/131、求下列函数的 (-1≤x≤ 1)最大
值 、最小值 。
二)基础练习:2、 (-1≤x≤ 1)的最小值是 。3、(2003·北京春招)设M和m分别表示
的最大值和最小值,则M+m
等于( )D2019/3/13三)典型应用【例1】已知函数y=3cosx-2,求该函数的最值?变式1:若x ?变式2:y= 求y的最值? 最大值为 1 最小值为-5最大值为 1 , 最小值为无最大值, 无最小值2019/3/13变式3:若 求该函数最值? 变式4:若 求该函数最值?无最大值, 无最小值无最大值, 无最小值2019/3/13变式5:
已知函数f(x)=cos4x–2sinxcosx–sin4x,
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若x∈[0, ],求f(x)的最大值、最小值.解析:(Ⅰ)因为 与例1有何关系?2019/3/132019/3/13【例2】已知 函数y=2sinx+3cosx ,求该函数的最值?变式1:一般地y=a sinx+b cosx,其中a、b 为已知实数,a、b为任意实数,求其最值?最大值为 最小值为-最大值为 最小值为-2019/3/13【例3】 已知 ,求该函数的最值? 变式1:已知
求该函数的最值?变式练习:已知
求该函数的最值? 最大值为 最小值为最大值为 5 最小值为12019/3/13典型例题【例4】 已知函数
求该函数最值?
法一)解析:(法一):函数
的几何意义为两点 连线的斜率k,而Q点的轨迹为单位圆,则有:
2019/3/13 (法二): 2019/3/13变式1:已知函数
求函数的最值?最大值为 , 最小值为2019/3/131、已知 ,则( )
A、函数最小值为–2,最大值为0
B、函数的最小值为–4
C、函数无最小值,最大值为0
D、函数最小值为–4,最大值为4 C2、已知, 求函数的最小值是 。
四)巩固测试小试身手2019/3/133.已知 求
的最值?4.求 的最值?5.设x、y满足x2 + y2 =1,求 3x+4y 的最大值? 最大值为 1, 最小值0最大值为5最大值为 最小值为2019/3/13课外作业:1、函数y=(sinx+1)(cosx+1)的最大值和最小值
分别是 、 .2019/3/132、设函数y=acosx+b(a,b为常数且a>0)的最大值为1,最小值为–7,那么acosx+bsinx的最大值为 ( )
A、3 B、4 C、5 D、63、设函数y=4sinx cosx+sin2x+1,求y的最值?2019/3/13五、课堂小结1、化为一个角的三角函数,再利用有界性求最值 2?、配方法求最值:转化为二次函数在闭区间上
的最值问题,一、 如求函数 二、如 同时出现的题型。
用换元法解决 5、换元法求最值尤其是三角换元3、分离常数法,解决形如 型的函数。4、数形结合,解决形如 型的函数。6、利用不等式单调性求最值2019/3/13六)作业: P69 T8-T11-T12
