数学:1.3《相似三角形》课件(新人教版a选修4-1)
文档属性
| 名称 | 数学:1.3《相似三角形》课件(新人教版a选修4-1) |  | |
| 格式 | rar | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:11:00 | ||
图片预览




文档简介
课件23张PPT。2019/3/13人教A版高中数学选修4-1
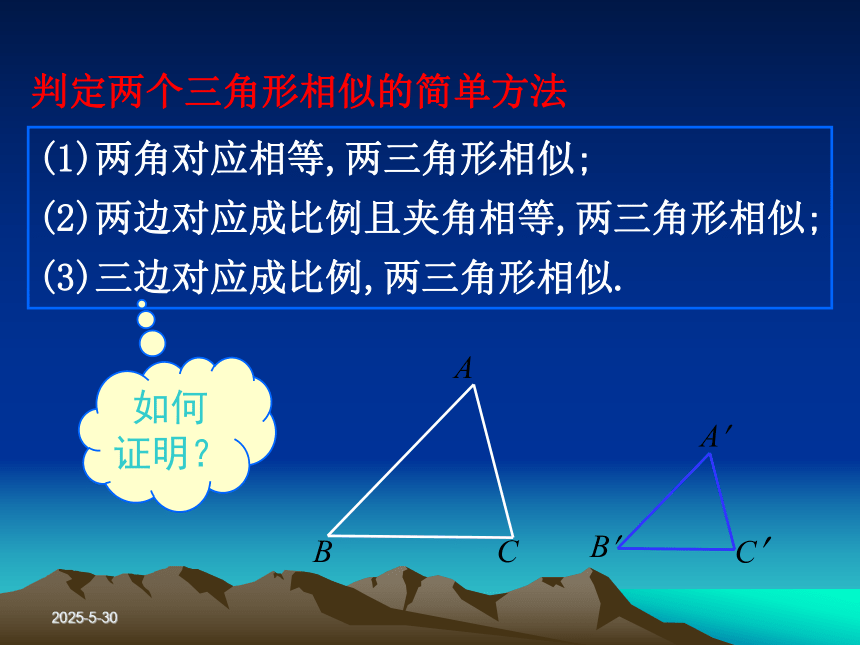
多媒体课件2019/3/13相似三角形的判定2019/3/13相似三角形的定义对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似的系数).复习回顾2019/3/13判定两个三角形相似的简单方法(1)两角对应相等,两三角形相似;
(2)两边对应成比例且夹角相等,两三角形相似;
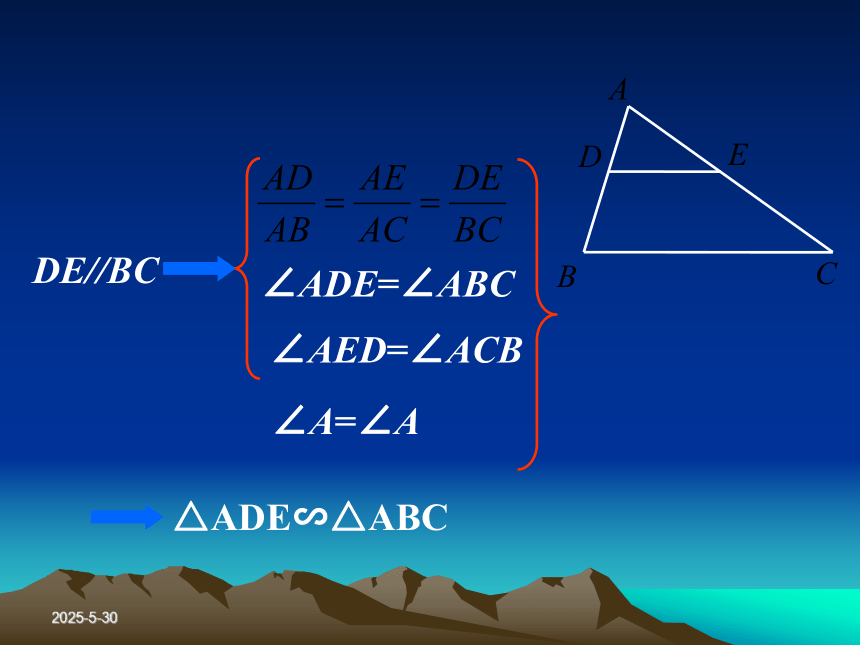
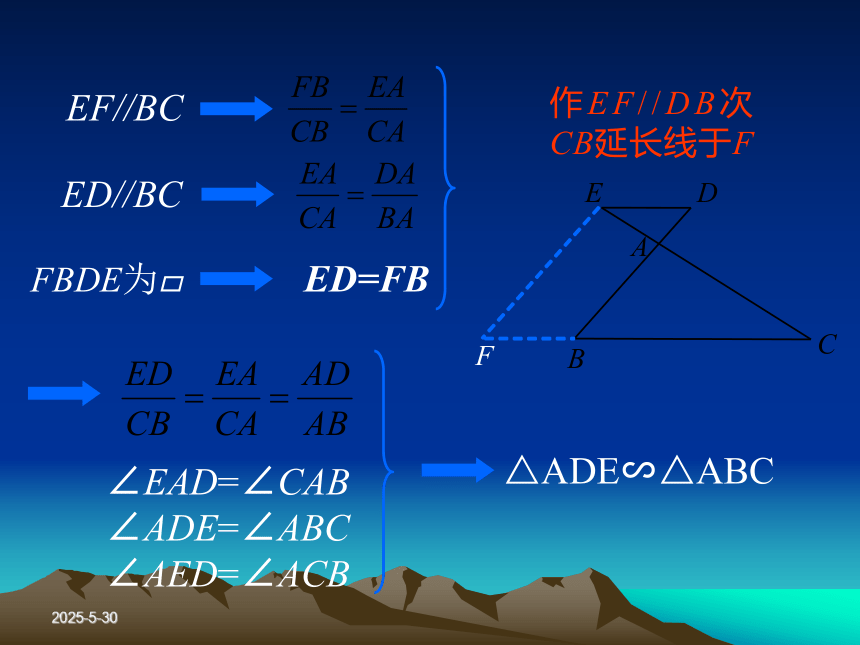
(3)三边对应成比例,两三角形相似.如何 证明?2019/3/132019/3/13∠EAD=∠CAB
∠ADE=∠ABC
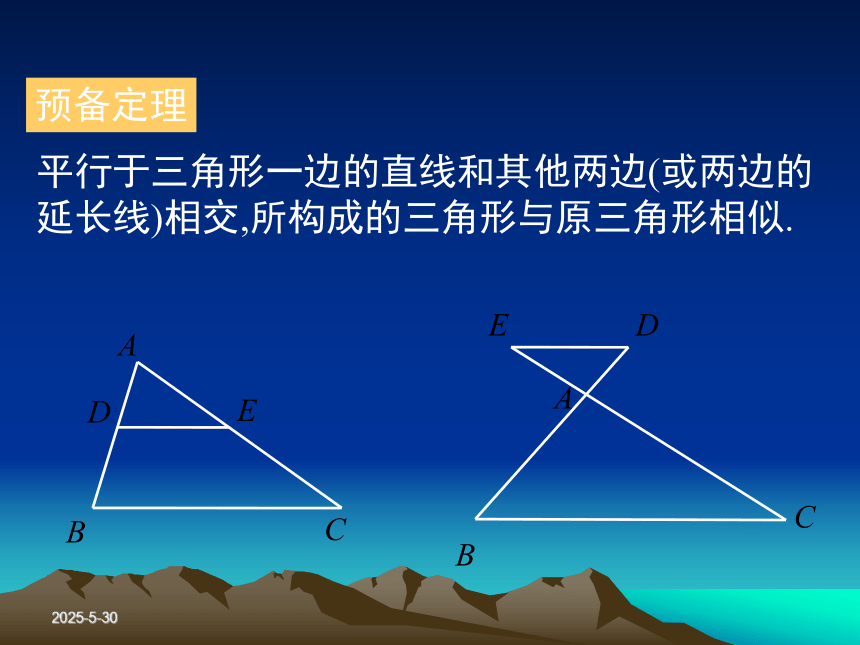
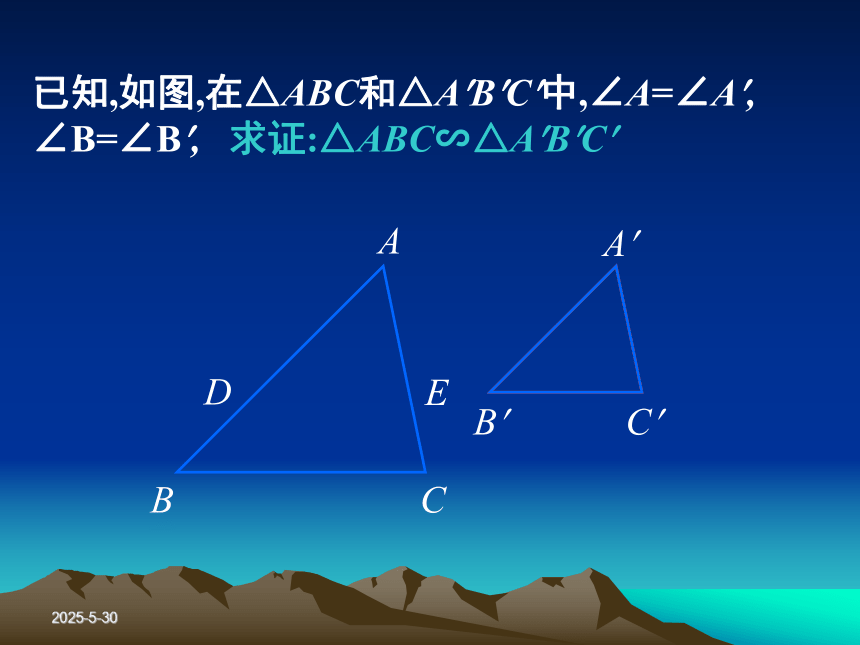
∠AED=∠ACB作EF//DB次CB延长线于F2019/3/13预备定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2019/3/13判定定理1对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述:两角对应相等,两三角形相似2019/3/13已知,如图,在△ABC和△A?B?C?中,∠A=∠A?, ∠B=∠B?, 求证:△ABC∽△A?B?C?2019/3/13证明: 在△ABC的边AB(或AB的延长线)上,截取AD=A’B’,过点D作DE//BC,交AC于点E.由预备定理得:
△ADE∽△ABC
∵∠ADE=∠B,∠B=∠B?
∴∠ADE=∠B?
∵∠A=∠A?, AD=A?B?
∴△ADE≌△A?B?C?
∴△A?B?C?∽△ABC2019/3/13例 如图,在△ABC, AB=AC, D是AC边上一点, BD=BC. 求证: BC2=AC?CD分析: 遇到线段的比例问题可以考虑三角形的相似证明:∵△ABC是等腰三角形
∴∠A=180?-2∠C
∵△BCD是等腰三角形
∴∠DBC=180?-2∠C
∴∠DBC=∠A
又∵∠C为公共角
∴△ABC∽△BDC即 BC2=AC?CD2019/3/13如图,圆内接△ABC的角平分线CD延长后交圆于一点E.分析: 遇到线段的比例问题可以考虑三角形的相似
根据线段所在三角形考虑证
△EBD∽△ECB练一练2019/3/13判定定理2对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述:两边对应成比例且夹角相等,两三角形相似2019/3/13△ADE≌△A?B?C??DE//BC2019/3/13证明: 作 DE?//BC,交AC于E?∴AE=AE?因此E与点E?重合即DE?与DE重合, 所以 DE//BC采用了“同一法”的间接证明引理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.2019/3/13当一个命题的条件和结论所指的概念唯一存在时,若直接证明有困难,就不妨改为去证它的逆否命题,然后根据唯一性的原理断言命题为真,这种解题方法叫做同一法 用同一法解题一般有三个步骤
①先作出一个符合结论的图形,然后推证出所作的图形符合已知条件;
②根据唯一性,证明所作出的图形与已知的图形是全等的或重合的;?
③从而说明已知图形符合结论. 2019/3/13例 如图,在△ABC内任取一点D,连接AD和BD.点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB. 求证: △DBE∽△ABC.2019/3/13判定定理3对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述:三边对应成比例,两三角形相似2019/3/13已知:如图,在△ABC和△A?B?C?中求证: △ABC∽△A’B’C’证明: 在△ABC的边AB(或延长线)上截取AD=A?B?,过点D作DE//BC,交AC于点E.△ADE∽△ABC∵ AD=A?B?∴△ADE≌△A?B?C?∴△ABC∽△A?B?C?2019/3/13例 如图,已知D、E、F分别是△ABC三边、BC、CA、AB的中点. 求证:△DEF∽△ABC证明:∵线段EF、FD、DE都是△ABC的中位线∴△DEF∽△ABC2019/3/13直角三角形相似的判定定理如果两个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(1)如果两个直角三角形有一个锐角对应相等,那么它们相似;
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.2019/3/13例 如图,已知AD、BE分别是△ABC中BC边和AC边上的高,H是AD、BE的交点求证:(1)AD?BC=BE?AC
(2)AH?HD=BH?HE分析: (1)只要证明Rt△ADC∽Rt△BEC
(2)只要证明Rt△AHE∽Rt△BHD2019/3/13小结相似三角形的概念预备定理判定定理3判定定理2判定定理1直角三角形判定定理
多媒体课件2019/3/13相似三角形的判定2019/3/13相似三角形的定义对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似的系数).复习回顾2019/3/13判定两个三角形相似的简单方法(1)两角对应相等,两三角形相似;
(2)两边对应成比例且夹角相等,两三角形相似;
(3)三边对应成比例,两三角形相似.如何 证明?2019/3/132019/3/13∠EAD=∠CAB
∠ADE=∠ABC
∠AED=∠ACB作EF//DB次CB延长线于F2019/3/13预备定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2019/3/13判定定理1对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述:两角对应相等,两三角形相似2019/3/13已知,如图,在△ABC和△A?B?C?中,∠A=∠A?, ∠B=∠B?, 求证:△ABC∽△A?B?C?2019/3/13证明: 在△ABC的边AB(或AB的延长线)上,截取AD=A’B’,过点D作DE//BC,交AC于点E.由预备定理得:
△ADE∽△ABC
∵∠ADE=∠B,∠B=∠B?
∴∠ADE=∠B?
∵∠A=∠A?, AD=A?B?
∴△ADE≌△A?B?C?
∴△A?B?C?∽△ABC2019/3/13例 如图,在△ABC, AB=AC, D是AC边上一点, BD=BC. 求证: BC2=AC?CD分析: 遇到线段的比例问题可以考虑三角形的相似证明:∵△ABC是等腰三角形
∴∠A=180?-2∠C
∵△BCD是等腰三角形
∴∠DBC=180?-2∠C
∴∠DBC=∠A
又∵∠C为公共角
∴△ABC∽△BDC即 BC2=AC?CD2019/3/13如图,圆内接△ABC的角平分线CD延长后交圆于一点E.分析: 遇到线段的比例问题可以考虑三角形的相似
根据线段所在三角形考虑证
△EBD∽△ECB练一练2019/3/13判定定理2对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述:两边对应成比例且夹角相等,两三角形相似2019/3/13△ADE≌△A?B?C??DE//BC2019/3/13证明: 作 DE?//BC,交AC于E?∴AE=AE?因此E与点E?重合即DE?与DE重合, 所以 DE//BC采用了“同一法”的间接证明引理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.2019/3/13当一个命题的条件和结论所指的概念唯一存在时,若直接证明有困难,就不妨改为去证它的逆否命题,然后根据唯一性的原理断言命题为真,这种解题方法叫做同一法 用同一法解题一般有三个步骤
①先作出一个符合结论的图形,然后推证出所作的图形符合已知条件;
②根据唯一性,证明所作出的图形与已知的图形是全等的或重合的;?
③从而说明已知图形符合结论. 2019/3/13例 如图,在△ABC内任取一点D,连接AD和BD.点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB. 求证: △DBE∽△ABC.2019/3/13判定定理3对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述:三边对应成比例,两三角形相似2019/3/13已知:如图,在△ABC和△A?B?C?中求证: △ABC∽△A’B’C’证明: 在△ABC的边AB(或延长线)上截取AD=A?B?,过点D作DE//BC,交AC于点E.△ADE∽△ABC∵ AD=A?B?∴△ADE≌△A?B?C?∴△ABC∽△A?B?C?2019/3/13例 如图,已知D、E、F分别是△ABC三边、BC、CA、AB的中点. 求证:△DEF∽△ABC证明:∵线段EF、FD、DE都是△ABC的中位线∴△DEF∽△ABC2019/3/13直角三角形相似的判定定理如果两个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(1)如果两个直角三角形有一个锐角对应相等,那么它们相似;
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.2019/3/13例 如图,已知AD、BE分别是△ABC中BC边和AC边上的高,H是AD、BE的交点求证:(1)AD?BC=BE?AC
(2)AH?HD=BH?HE分析: (1)只要证明Rt△ADC∽Rt△BEC
(2)只要证明Rt△AHE∽Rt△BHD2019/3/13小结相似三角形的概念预备定理判定定理3判定定理2判定定理1直角三角形判定定理
