数学:2.3.2《抛物线的简单几何性质》课件(新人教版a选修1-1)
文档属性
| 名称 | 数学:2.3.2《抛物线的简单几何性质》课件(新人教版a选修1-1) |  | |
| 格式 | rar | ||
| 文件大小 | 134.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:13:00 | ||
图片预览




文档简介
(共15张PPT)
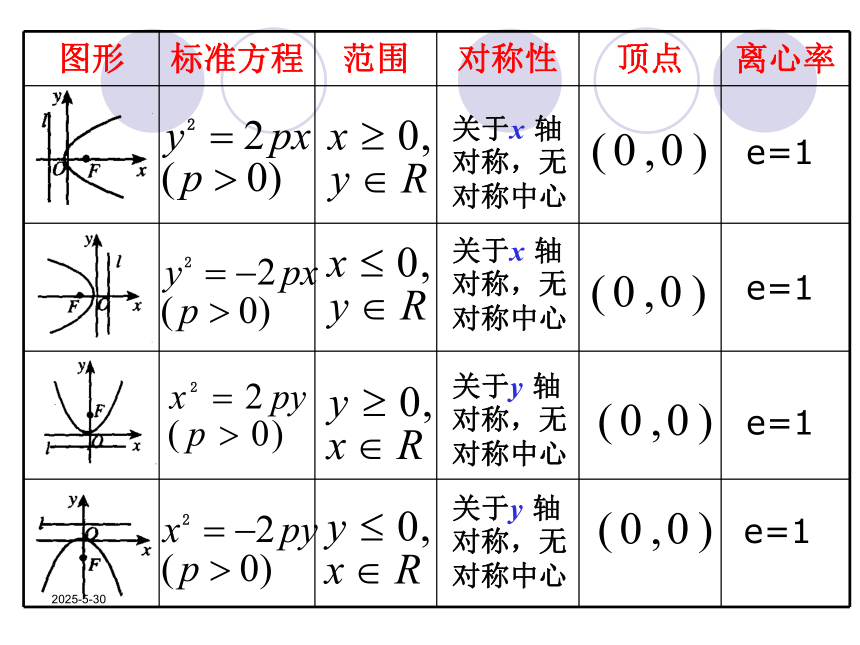
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称,无
对称中心
关于x 轴
对称,无
对称中心
关于y 轴
对称,无
对称中心
关于y 轴
对称,无
对称中心
e=1
e=1
e=1
e=1
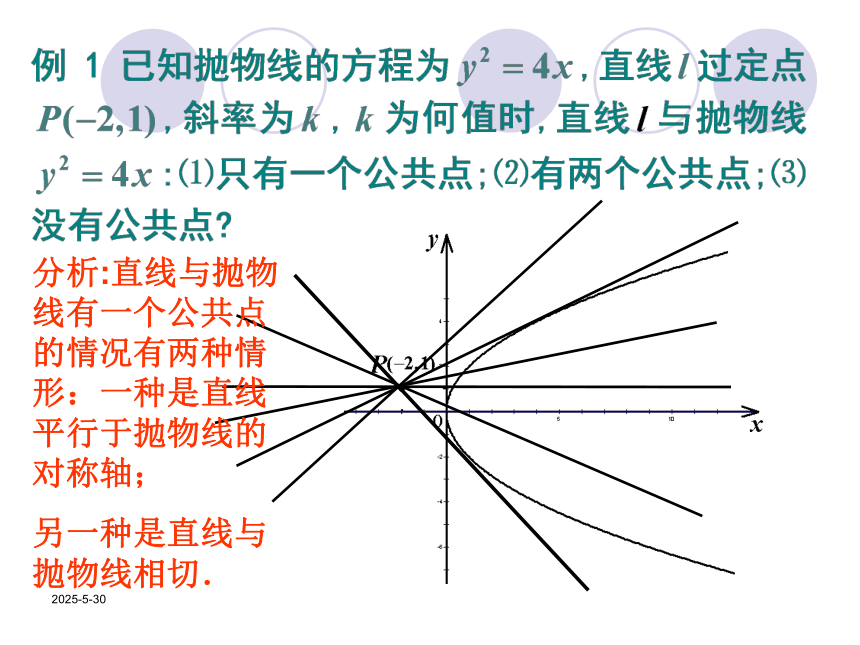
分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切.
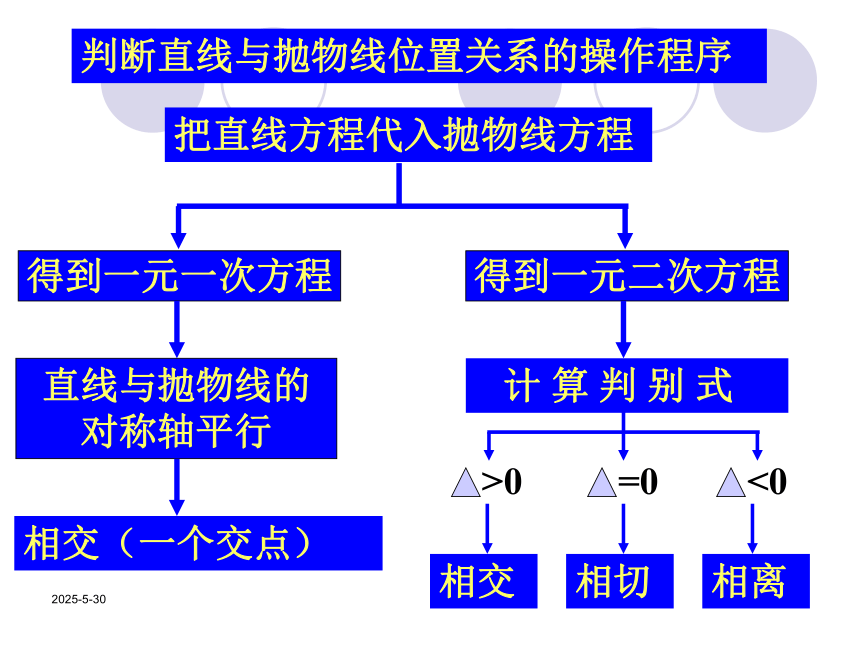
判断直线与抛物线位置关系的操作程序
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
分析:
直线与抛物线有两个公共点时△>0
分析:
直线与抛物线没有公共点时△<0
注:在方程中,二次项系数含有k,所以要对k进行讨论
作图要点:画出直线与抛物线只有一个公共点时的情形,观察直线绕点P转动的情形
变式一:已知抛物线方程y2=4x,当b为何值时,直线l:y=x+b与抛物线(1)只有一个公共点(2)两个公共点(3)没有公共点.当直线与抛物线有公共点时,b的最大值是多少
分析:本题与例1类型相似,方法一样,通过联立方程组求得.
(1)b=1 (2)b<1
(3)b>1,当直线与抛物线有公共点时,b的最大值当直线与抛物线相切时取得.其值为1
变式二:已知实数x、y满足方程y2=4x,求函数
的最值
变式三:点(x,y)在抛物线y2=4x上运动,求函数z=x-y的最值.
本题转化为过定点(-2,1)的直线与抛物线有公共点时斜率的最值问题.
本题转化为直线y=x-z与抛物线有公共点时z的最值问题.
无最大值
x
y
B
A
F
O
解:因为直线AB过定点F且不与x轴平
行,设直线AB的方程为
x
y
B
A
F
O
x
y
B
A
F
O
x
y
B
A
F
O
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称,无
对称中心
关于x 轴
对称,无
对称中心
关于y 轴
对称,无
对称中心
关于y 轴
对称,无
对称中心
e=1
e=1
e=1
e=1
分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切.
判断直线与抛物线位置关系的操作程序
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
分析:
直线与抛物线有两个公共点时△>0
分析:
直线与抛物线没有公共点时△<0
注:在方程中,二次项系数含有k,所以要对k进行讨论
作图要点:画出直线与抛物线只有一个公共点时的情形,观察直线绕点P转动的情形
变式一:已知抛物线方程y2=4x,当b为何值时,直线l:y=x+b与抛物线(1)只有一个公共点(2)两个公共点(3)没有公共点.当直线与抛物线有公共点时,b的最大值是多少
分析:本题与例1类型相似,方法一样,通过联立方程组求得.
(1)b=1 (2)b<1
(3)b>1,当直线与抛物线有公共点时,b的最大值当直线与抛物线相切时取得.其值为1
变式二:已知实数x、y满足方程y2=4x,求函数
的最值
变式三:点(x,y)在抛物线y2=4x上运动,求函数z=x-y的最值.
本题转化为过定点(-2,1)的直线与抛物线有公共点时斜率的最值问题.
本题转化为直线y=x-z与抛物线有公共点时z的最值问题.
无最大值
x
y
B
A
F
O
解:因为直线AB过定点F且不与x轴平
行,设直线AB的方程为
x
y
B
A
F
O
x
y
B
A
F
O
x
y
B
A
F
O
