比例综合应用题(专项训练含答案)2023-2024学年数学六年级下册青岛版
文档属性
| 名称 | 比例综合应用题(专项训练含答案)2023-2024学年数学六年级下册青岛版 |

|
|
| 格式 | docx | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 21:56:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
比例综合应用题(专项训练)2023-2024学年数学六年级下册青岛版
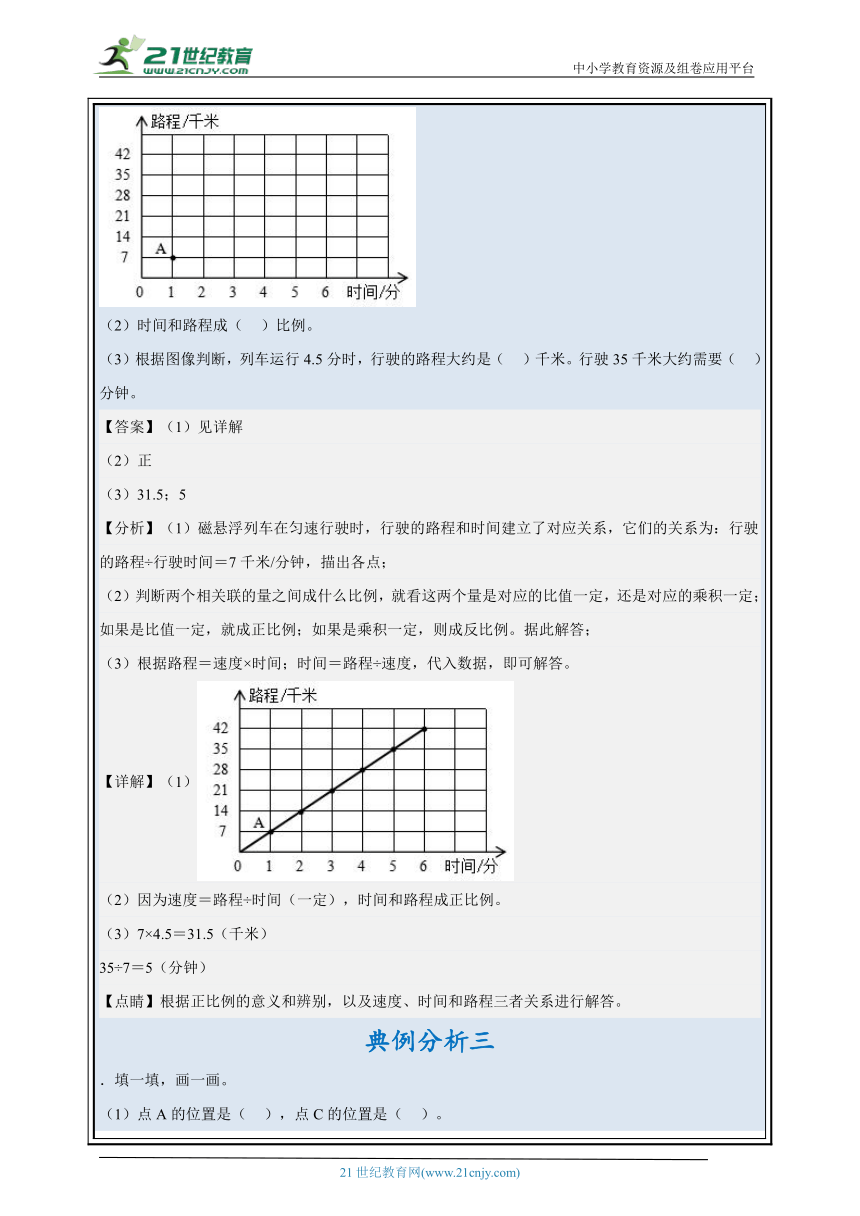
典例分析一 .在一幅比例尺是1∶500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1∶250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解) 【答案】13.6厘米 【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺;代入数据,求出甲、乙两地的实际距离;设画在新图上时甲、乙两地的距离是x厘米;1∶250000=x∶甲、乙两地的实际距离,解比例,即可解答。 【详解】6.8÷ =6.8×500000 =3400000(厘米) 解:设画在新图上时甲、乙两地的距离是x厘米。 1∶250000=x∶3400000 250000x=3400000×1 x=3400000÷250000 x=13.6 答:画在新图纸上时甲、乙两地的距离是13.6厘米。 【点睛】根据图上距离、比例尺、实际距离三者的关系,进行分析解答即可得出结论。 典例分析二 .磁悬浮列车匀速行驶时,路程与时间的关系如下。 时间/分1234567…路程/千米7142128354249…
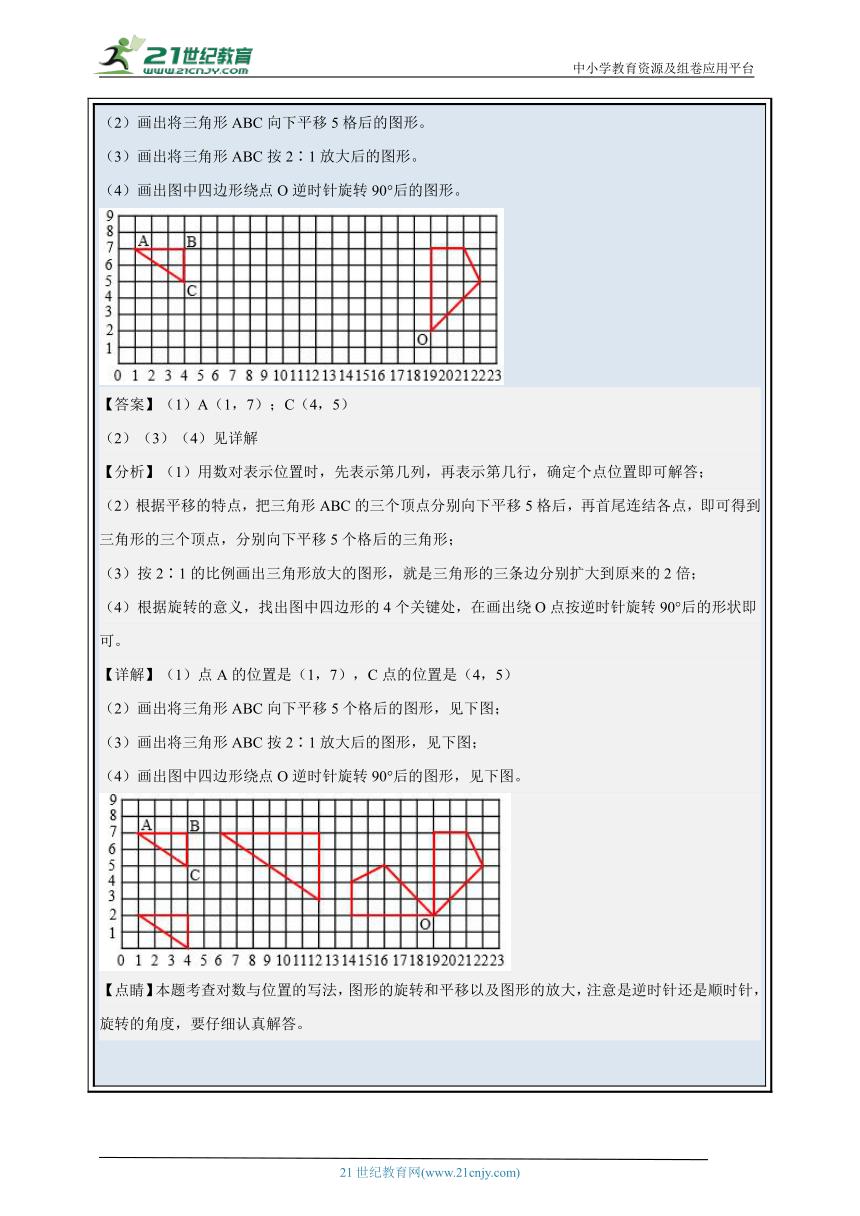
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。 (2)时间和路程成( )比例。 (3)根据图像判断,列车运行4.5分时,行驶的路程大约是( )千米。行驶35千米大约需要( )分钟。 【答案】(1)见详解 (2)正 (3)31.5;5 【分析】(1)磁悬浮列车在匀速行驶时,行驶的路程和时间建立了对应关系,它们的关系为:行驶的路程÷行驶时间=7千米/分钟,描出各点; (2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答; (3)根据路程=速度×时间;时间=路程÷速度,代入数据,即可解答。 【详解】(1) (2)因为速度=路程÷时间(一定),时间和路程成正比例。 (3)7×4.5=31.5(千米) 35÷7=5(分钟) 【点睛】根据正比例的意义和辨别,以及速度、时间和路程三者关系进行解答。 典例分析三 .填一填,画一画。 (1)点A的位置是( ),点C的位置是( )。 (2)画出将三角形ABC向下平移5格后的图形。 (3)画出将三角形ABC按2∶1放大后的图形。 (4)画出图中四边形绕点O逆时针旋转90°后的图形。 【答案】(1)A(1,7);C(4,5) (2)(3)(4)见详解 【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,确定个点位置即可解答; (2)根据平移的特点,把三角形ABC的三个顶点分别向下平移5格后,再首尾连结各点,即可得到三角形的三个顶点,分别向下平移5个格后的三角形; (3)按2∶1的比例画出三角形放大的图形,就是三角形的三条边分别扩大到原来的2倍; (4)根据旋转的意义,找出图中四边形的4个关键处,在画出绕O点按逆时针旋转90°后的形状即可。 【详解】(1)点A的位置是(1,7),C点的位置是(4,5) (2)画出将三角形ABC向下平移5个格后的图形,见下图; (3)画出将三角形ABC按2∶1放大后的图形,见下图; (4)画出图中四边形绕点O逆时针旋转90°后的图形,见下图。 【点睛】本题考查对数与位置的写法,图形的旋转和平移以及图形的放大,注意是逆时针还是顺时针,旋转的角度,要仔细认真解答。
跟踪训练
1.李师傅要加工900个零件,前4天加工了240个。照这样的效率,还要多少天才能完成任务?
2.一个晒盐场用100克海水可以晒出3克盐。照这样计算,一个晒盐场如果一次放入3000吨海水,可以晒出多少吨盐?
3.生产一批零件,原计划每天生产240个,25天可以完成,实际每天多生产60个,实际多少天完成?(用比例解答)
4.从济南到郑州的公路长440千米。一辆中巴车2小时行了160千米,照这样计算,从济南到郑州需要几小时?(用比例解)
5.端午节圆圆一家四口开车去距离560千米的奶奶家。汽车每行100千米耗油8升,按照这个耗油量,出发时油箱内有60升汽油,途中不加油能到达奶奶家吗?(用比例法解)
6.在一幅比例尺是1∶500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1∶250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
7.给一间小型会议室铺地砖,用面积0.09m2的方砖铺地,正好需要100块,如果改用边长0.2m的方砖铺地,需要多少块?
8.六年级同学做广播体操,如果每行站18人,可以站10行,如果每行站12人,可以站多少行?(用比例来解)
9.下面是新鲜赣南脐橙中维生素C的含量情况。
赣南脐橙质量(克) 1 2 3 4 5 6
维生素C含量(毫克) 4.1 8.2 12.3 16.4 20.5 24.6
(1)根据表中的信息可以判断,赣南脐橙质量与维生素C含量成( )比例;
(2)在下图中描出赣南脐橙质量和维生素C含量相对应的点,然后把它们按顺序连接起来;
(3)根据图像估计4.5克新鲜赣南脐橙含有维生素C( )毫克。
10.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 7 …
路程/千米 7 14 21 28 35 42 49 …
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)时间和路程成( )比例。
(3)根据图像判断,列车运行4.5分时,行驶的路程大约是( )千米。行驶35千米大约需要( )分钟。
11.某造纸厂生产情况如下表,根据表格回答问题。
时间(天) 2 4 5 7 8 9
生产量(吨) 140 280 350 490 560 630
(1)在下图中描出表示时间与生产量相对应的点,然后将它们连起来。
(2)该造纸厂6月份的产量是( )吨。
(3)根据上图,该造纸厂的生产量与时间成什么比例?请写出你的理由。
12.在方格中根据要求画一面。(每格看作边长是1厘米的正方形)
(1)一个三角形,三个顶点的位置分别表示为A(1,1)、B(4,1)、C(1,3)。请画出这个三角形,并标注字母。
(2)将三角形绕B点顺时针旋转90°,画出旋转后的图形。
(3)将原三角形按2∶1的比放大画出放大后的三角形。放大后三角形的面积与原三角形面积的比是( )。
(4)根据原来的三角形与放大后的三角形边的关系写出一组比例式是( )。
13.2022年第24届冬季奥运会在北京和张家口举办,北京至张家口的距离约是180千米,在一幅冬奥会宣传图上,两地间的图上距离是60厘米。
(1)这幅宣传图的比例尺是多少?
(2)在这幅宣传图上京张高铁全线长58厘米,京张高铁实际全线长多少千米?
14.如图,宁宁家距书店1000米。
(1)这幅图的比例尺是多少?
(2)宁宁家到学校的实际距离是多少米?
(3)现要在宁宁家南偏西45°方向1500米处建一个体育馆,请在图中画出体育馆的位置。
参考答案:
1.11天
【分析】把还需要的天数设为未知数,由“工作效率=工作总量÷工作时间”可知,剩下零件的数量∶还需要的天数=已经生产的零件数量∶已经用的天数,据此解答。
【详解】解:设还要x天才能完成任务。
(900-240)∶x=240∶4
660∶x=240∶4
240x=660×4
240x=2640
x=2640÷240
x=11
答:还要11天才能完成任务。
【点睛】本题主要考查比例的应用,掌握工作总量、工作时间、工作效率之间的关系是解答题目的关键。
2.90吨
【分析】由题意可知:每克海水晒出多少克盐是一定的,即海水的质量与盐的质量之间的比值是一定的,则海水的质量与盐的质量成正比例,据此即可列比例求解。
【详解】解:设可以晒出x吨盐,
3000∶x=100∶3
x×100=3000×3
100x=9000
x=9000÷100
x=90
答:可以晒出90吨盐。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
3.20天
【分析】设实际x天完成,根据每天生产数量×对应天数=总数量(一定),列出反比例算式解答即可。
【详解】解:设实际x天完成。
(240+60)x=240×25
300x÷300=6000÷300
x=20
答:实际20天完成。
【点睛】关键是确定比例关系,相关联的两个量积一定是反比例关系。
4.5.5小时
【分析】由题意可知,这辆车的速度不变,则路程与时间成正比例关系,根据“速度=路程÷时间”列方程解答即可。
【详解】解:设从济南到郑州需要小时。
答:从济南到郑州需要5.5小时。
【点睛】本题主要考查应用比例知识解决实际问题,掌握路程、时间、速度之间的关系是解答题目的关键。
5.能
【分析】由题意可知,汽车每行100千米耗油8升,1升油能够行驶的路程是一定的,所以路程与油的升数成正比例,据此列比例求出行驶560千米需要汽油的升数,然后与60升汽油对比即可。
【详解】解:设汽车行驶560千米需要耗油x升。
100∶8=560∶x
100x=8×560
100x=4480
x=44.8
44.8<60
答:途中不加油能到达奶奶家。
【点睛】本题考查用比例解决问题,明确1升油能够行驶的路程是一定的是解题的关键。
6.13.6厘米
【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺;代入数据,求出甲、乙两地的实际距离;设画在新图上时甲、乙两地的距离是x厘米;1∶250000=x∶甲、乙两地的实际距离,解比例,即可解答。
【详解】6.8÷
=6.8×500000
=3400000(厘米)
解:设画在新图上时甲、乙两地的距离是x厘米。
1∶250000=x∶3400000
250000x=3400000×1
x=3400000÷250000
x=13.6
答:画在新图纸上时甲、乙两地的距离是13.6厘米。
【点睛】根据图上距离、比例尺、实际距离三者的关系,进行分析解答即可得出结论。
7.225块
【分析】根据题意可知,会议室的面积是一定的,一块方砖的面积和方砖的块数成反比例,设需要x块;列方程:0.09×100=0.2×0.2x,解方程即可。
【详解】解:设需要x块。
0.09×100=0.2×0.2×x
0.04x=9
x=9÷0.04
x=225
答:需要225块。
【点睛】利用方砖的面积与块数成反比,设出未知数,列方程,解方程。
8.15行
【分析】由题意可知,六年级的学生的总人数不变,则每行站的人数和行数成反比例关系,据此列比例即可。
【详解】解:设可以站x行。
18×10=12x
12x=180
x=15
答:可以站15行。
【点睛】本题考查用比例解决问题,准确判断题目里的比例关系是解题的关键。
9.(1)正;(2)见详解;(3)18.45
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)利用统计表中的数据描点、连线即可;
(3)4.5×4.1计算即可。
【详解】(1)因为赣南脐橙质量与维生素C含量的比值一定,所以成正比例;
(2)
(3)4.5×4.1=18.45
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
10.(1)见详解
(2)正
(3)31.5;5
【分析】(1)磁悬浮列车在匀速行驶时,行驶的路程和时间建立了对应关系,它们的关系为:行驶的路程÷行驶时间=7千米/分钟,描出各点;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答;
(3)根据路程=速度×时间;时间=路程÷速度,代入数据,即可解答。
【详解】(1)
(2)因为速度=路程÷时间(一定),时间和路程成正比例。
(3)7×4.5=31.5(千米)
35÷7=5(分钟)
【点睛】根据正比例的意义和辨别,以及速度、时间和路程三者关系进行解答。
11.(1)见详解;
(2)2100;
(3)正比例;见详解
【分析】(1)折线统计图的绘制方法是:先整理数据;利用纵轴和横轴上的长度单位所表示的数量,根据数量的多少描出各点,再把各点用线段顺次连接起来。
(2)根据统计表上的数据,造纸厂的生产量为140吨,工作时间是2天,用工作总量÷工作时间=工作效率,求出造纸厂1天的生产量,6月份共有30天,再用1天的生产量乘30,即可求出该造纸厂6月份的产量。
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)如图:
(2)140÷2×30
=70×30
=2100(吨)
即该造纸厂6月份的产量是2100吨。
(3)(吨)
说明生产量与时间的比值一定,符合正比例的意义。
答:该造纸厂的生产量与时间成正比例,因为生产量与时间的比值一定,所以它们之间成正比例。
【点睛】此题考查折线统计图的应用以及辨识成正、反比例的量,主要看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(1)见详解;(2)见详解;(3)见详解;4∶1(4)1∶4=2∶8(答案不唯一)
【分析】(1)数对的表示方法:(列数,行数),根据数对找出A、B、C各点在方格中的对应位置,依次连接各点,并在图中标注各点名称,据此解答。
(2)根据旋转的特征,将三角形绕B点顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)把三角形ABC按2∶1扩大,即三角形的每一条边扩大到原来的2倍,原三角形的底和高分别乘3,得出扩大后三角形的底和高,据此画出扩大后的图形。再根据三角形的面积公式,分别求出原来的三角形和扩大后的三角形的面积,利用比的意义,即可求出放大后三角形的面积与原三角形面积的比。
(4)根据(3)求出的放大后三角形的面积与原三角形面积的比,即可求出比值,根据比例的意义:表示两个比值相等的式子,据此即可写出比例。
【详解】(1)(2)(3)作图如下:
3×2÷2=3(平方厘米)
3×2=6(厘米)
2×2=4(厘米)
6×4÷2=12(平方厘米)
放大后三角形的面积∶原三角形面积的比=12∶3=4∶1。
(4)因为原三角形面积∶放大后三角形的面积=1∶4,
可得1∶4=,,所以可写比例:1∶4=2∶8(答案不唯一)
【点睛】此题主要考查根据数对找位置、图形的旋转、图形的放大与缩小以及比和比例的意义。
13.(1)1∶300000;
(2)174千米。
【分析】(1)根据比例尺的定义,比例尺是图上距离与实际距离的比,把图上距离与实际距离的单元统一一下代入公式即可得解;
(2)根据(1)中得出的比例尺,利用比例的性质即可得解。
【详解】(1)180千米=18000000厘米
60∶18000000=1∶300000
答:这幅宣传图的比例尺是1∶300000。
(2)图上1厘米表示300000厘米,即1厘米表示3千米,
3×58=174(千米)
答:京张高铁实际全线长174千米。
14.(1)1∶50000;
(2)2000米;
(3)见详解
【分析】(1)通过直尺测量,宁宁家到书店的图上距离是2厘米,宁宁家距书店1000米,统一单位后,根据比例尺的意义,比例尺=图上距离∶实际距离,代入数据求出这幅图的比例尺。
(2)经测量,宁宁家到学校的图上距离是4厘米,根据实际距离=图上距离÷比例尺,代入数据即可求出宁宁家到学校的实际距离是多少米。
(3)统一单位后,用实际距离×比例尺=图上距离,求出体育馆和宁宁家两地之间的图上距离,再以宁宁家为观测点,利用地图上的方向“上北下南,左西右东”,根据方向、角度、距离确定体育馆的位置,并在图上标注出来。
【详解】(1)1000米=100000厘米
2∶100000=1∶50000
答:这幅图的比例尺是1∶50000。
(2)4÷
=4×50000
=200000(厘米)
200000厘米=2000米
答:宁宁家到学校的实际距离是2000米。
(3)1500米=150000厘米
150000×=3(厘米)
如图:
【点睛】此题主要考查比例尺的意义以及根据方向、角度、距离确定物体的位置。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
比例综合应用题(专项训练)2023-2024学年数学六年级下册青岛版
典例分析一 .在一幅比例尺是1∶500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1∶250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解) 【答案】13.6厘米 【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺;代入数据,求出甲、乙两地的实际距离;设画在新图上时甲、乙两地的距离是x厘米;1∶250000=x∶甲、乙两地的实际距离,解比例,即可解答。 【详解】6.8÷ =6.8×500000 =3400000(厘米) 解:设画在新图上时甲、乙两地的距离是x厘米。 1∶250000=x∶3400000 250000x=3400000×1 x=3400000÷250000 x=13.6 答:画在新图纸上时甲、乙两地的距离是13.6厘米。 【点睛】根据图上距离、比例尺、实际距离三者的关系,进行分析解答即可得出结论。 典例分析二 .磁悬浮列车匀速行驶时,路程与时间的关系如下。 时间/分1234567…路程/千米7142128354249…
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。 (2)时间和路程成( )比例。 (3)根据图像判断,列车运行4.5分时,行驶的路程大约是( )千米。行驶35千米大约需要( )分钟。 【答案】(1)见详解 (2)正 (3)31.5;5 【分析】(1)磁悬浮列车在匀速行驶时,行驶的路程和时间建立了对应关系,它们的关系为:行驶的路程÷行驶时间=7千米/分钟,描出各点; (2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答; (3)根据路程=速度×时间;时间=路程÷速度,代入数据,即可解答。 【详解】(1) (2)因为速度=路程÷时间(一定),时间和路程成正比例。 (3)7×4.5=31.5(千米) 35÷7=5(分钟) 【点睛】根据正比例的意义和辨别,以及速度、时间和路程三者关系进行解答。 典例分析三 .填一填,画一画。 (1)点A的位置是( ),点C的位置是( )。 (2)画出将三角形ABC向下平移5格后的图形。 (3)画出将三角形ABC按2∶1放大后的图形。 (4)画出图中四边形绕点O逆时针旋转90°后的图形。 【答案】(1)A(1,7);C(4,5) (2)(3)(4)见详解 【分析】(1)用数对表示位置时,先表示第几列,再表示第几行,确定个点位置即可解答; (2)根据平移的特点,把三角形ABC的三个顶点分别向下平移5格后,再首尾连结各点,即可得到三角形的三个顶点,分别向下平移5个格后的三角形; (3)按2∶1的比例画出三角形放大的图形,就是三角形的三条边分别扩大到原来的2倍; (4)根据旋转的意义,找出图中四边形的4个关键处,在画出绕O点按逆时针旋转90°后的形状即可。 【详解】(1)点A的位置是(1,7),C点的位置是(4,5) (2)画出将三角形ABC向下平移5个格后的图形,见下图; (3)画出将三角形ABC按2∶1放大后的图形,见下图; (4)画出图中四边形绕点O逆时针旋转90°后的图形,见下图。 【点睛】本题考查对数与位置的写法,图形的旋转和平移以及图形的放大,注意是逆时针还是顺时针,旋转的角度,要仔细认真解答。
跟踪训练
1.李师傅要加工900个零件,前4天加工了240个。照这样的效率,还要多少天才能完成任务?
2.一个晒盐场用100克海水可以晒出3克盐。照这样计算,一个晒盐场如果一次放入3000吨海水,可以晒出多少吨盐?
3.生产一批零件,原计划每天生产240个,25天可以完成,实际每天多生产60个,实际多少天完成?(用比例解答)
4.从济南到郑州的公路长440千米。一辆中巴车2小时行了160千米,照这样计算,从济南到郑州需要几小时?(用比例解)
5.端午节圆圆一家四口开车去距离560千米的奶奶家。汽车每行100千米耗油8升,按照这个耗油量,出发时油箱内有60升汽油,途中不加油能到达奶奶家吗?(用比例法解)
6.在一幅比例尺是1∶500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1∶250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
7.给一间小型会议室铺地砖,用面积0.09m2的方砖铺地,正好需要100块,如果改用边长0.2m的方砖铺地,需要多少块?
8.六年级同学做广播体操,如果每行站18人,可以站10行,如果每行站12人,可以站多少行?(用比例来解)
9.下面是新鲜赣南脐橙中维生素C的含量情况。
赣南脐橙质量(克) 1 2 3 4 5 6
维生素C含量(毫克) 4.1 8.2 12.3 16.4 20.5 24.6
(1)根据表中的信息可以判断,赣南脐橙质量与维生素C含量成( )比例;
(2)在下图中描出赣南脐橙质量和维生素C含量相对应的点,然后把它们按顺序连接起来;
(3)根据图像估计4.5克新鲜赣南脐橙含有维生素C( )毫克。
10.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 7 …
路程/千米 7 14 21 28 35 42 49 …
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)时间和路程成( )比例。
(3)根据图像判断,列车运行4.5分时,行驶的路程大约是( )千米。行驶35千米大约需要( )分钟。
11.某造纸厂生产情况如下表,根据表格回答问题。
时间(天) 2 4 5 7 8 9
生产量(吨) 140 280 350 490 560 630
(1)在下图中描出表示时间与生产量相对应的点,然后将它们连起来。
(2)该造纸厂6月份的产量是( )吨。
(3)根据上图,该造纸厂的生产量与时间成什么比例?请写出你的理由。
12.在方格中根据要求画一面。(每格看作边长是1厘米的正方形)
(1)一个三角形,三个顶点的位置分别表示为A(1,1)、B(4,1)、C(1,3)。请画出这个三角形,并标注字母。
(2)将三角形绕B点顺时针旋转90°,画出旋转后的图形。
(3)将原三角形按2∶1的比放大画出放大后的三角形。放大后三角形的面积与原三角形面积的比是( )。
(4)根据原来的三角形与放大后的三角形边的关系写出一组比例式是( )。
13.2022年第24届冬季奥运会在北京和张家口举办,北京至张家口的距离约是180千米,在一幅冬奥会宣传图上,两地间的图上距离是60厘米。
(1)这幅宣传图的比例尺是多少?
(2)在这幅宣传图上京张高铁全线长58厘米,京张高铁实际全线长多少千米?
14.如图,宁宁家距书店1000米。
(1)这幅图的比例尺是多少?
(2)宁宁家到学校的实际距离是多少米?
(3)现要在宁宁家南偏西45°方向1500米处建一个体育馆,请在图中画出体育馆的位置。
参考答案:
1.11天
【分析】把还需要的天数设为未知数,由“工作效率=工作总量÷工作时间”可知,剩下零件的数量∶还需要的天数=已经生产的零件数量∶已经用的天数,据此解答。
【详解】解:设还要x天才能完成任务。
(900-240)∶x=240∶4
660∶x=240∶4
240x=660×4
240x=2640
x=2640÷240
x=11
答:还要11天才能完成任务。
【点睛】本题主要考查比例的应用,掌握工作总量、工作时间、工作效率之间的关系是解答题目的关键。
2.90吨
【分析】由题意可知:每克海水晒出多少克盐是一定的,即海水的质量与盐的质量之间的比值是一定的,则海水的质量与盐的质量成正比例,据此即可列比例求解。
【详解】解:设可以晒出x吨盐,
3000∶x=100∶3
x×100=3000×3
100x=9000
x=9000÷100
x=90
答:可以晒出90吨盐。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
3.20天
【分析】设实际x天完成,根据每天生产数量×对应天数=总数量(一定),列出反比例算式解答即可。
【详解】解:设实际x天完成。
(240+60)x=240×25
300x÷300=6000÷300
x=20
答:实际20天完成。
【点睛】关键是确定比例关系,相关联的两个量积一定是反比例关系。
4.5.5小时
【分析】由题意可知,这辆车的速度不变,则路程与时间成正比例关系,根据“速度=路程÷时间”列方程解答即可。
【详解】解:设从济南到郑州需要小时。
答:从济南到郑州需要5.5小时。
【点睛】本题主要考查应用比例知识解决实际问题,掌握路程、时间、速度之间的关系是解答题目的关键。
5.能
【分析】由题意可知,汽车每行100千米耗油8升,1升油能够行驶的路程是一定的,所以路程与油的升数成正比例,据此列比例求出行驶560千米需要汽油的升数,然后与60升汽油对比即可。
【详解】解:设汽车行驶560千米需要耗油x升。
100∶8=560∶x
100x=8×560
100x=4480
x=44.8
44.8<60
答:途中不加油能到达奶奶家。
【点睛】本题考查用比例解决问题,明确1升油能够行驶的路程是一定的是解题的关键。
6.13.6厘米
【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺;代入数据,求出甲、乙两地的实际距离;设画在新图上时甲、乙两地的距离是x厘米;1∶250000=x∶甲、乙两地的实际距离,解比例,即可解答。
【详解】6.8÷
=6.8×500000
=3400000(厘米)
解:设画在新图上时甲、乙两地的距离是x厘米。
1∶250000=x∶3400000
250000x=3400000×1
x=3400000÷250000
x=13.6
答:画在新图纸上时甲、乙两地的距离是13.6厘米。
【点睛】根据图上距离、比例尺、实际距离三者的关系,进行分析解答即可得出结论。
7.225块
【分析】根据题意可知,会议室的面积是一定的,一块方砖的面积和方砖的块数成反比例,设需要x块;列方程:0.09×100=0.2×0.2x,解方程即可。
【详解】解:设需要x块。
0.09×100=0.2×0.2×x
0.04x=9
x=9÷0.04
x=225
答:需要225块。
【点睛】利用方砖的面积与块数成反比,设出未知数,列方程,解方程。
8.15行
【分析】由题意可知,六年级的学生的总人数不变,则每行站的人数和行数成反比例关系,据此列比例即可。
【详解】解:设可以站x行。
18×10=12x
12x=180
x=15
答:可以站15行。
【点睛】本题考查用比例解决问题,准确判断题目里的比例关系是解题的关键。
9.(1)正;(2)见详解;(3)18.45
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)利用统计表中的数据描点、连线即可;
(3)4.5×4.1计算即可。
【详解】(1)因为赣南脐橙质量与维生素C含量的比值一定,所以成正比例;
(2)
(3)4.5×4.1=18.45
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
10.(1)见详解
(2)正
(3)31.5;5
【分析】(1)磁悬浮列车在匀速行驶时,行驶的路程和时间建立了对应关系,它们的关系为:行驶的路程÷行驶时间=7千米/分钟,描出各点;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答;
(3)根据路程=速度×时间;时间=路程÷速度,代入数据,即可解答。
【详解】(1)
(2)因为速度=路程÷时间(一定),时间和路程成正比例。
(3)7×4.5=31.5(千米)
35÷7=5(分钟)
【点睛】根据正比例的意义和辨别,以及速度、时间和路程三者关系进行解答。
11.(1)见详解;
(2)2100;
(3)正比例;见详解
【分析】(1)折线统计图的绘制方法是:先整理数据;利用纵轴和横轴上的长度单位所表示的数量,根据数量的多少描出各点,再把各点用线段顺次连接起来。
(2)根据统计表上的数据,造纸厂的生产量为140吨,工作时间是2天,用工作总量÷工作时间=工作效率,求出造纸厂1天的生产量,6月份共有30天,再用1天的生产量乘30,即可求出该造纸厂6月份的产量。
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)如图:
(2)140÷2×30
=70×30
=2100(吨)
即该造纸厂6月份的产量是2100吨。
(3)(吨)
说明生产量与时间的比值一定,符合正比例的意义。
答:该造纸厂的生产量与时间成正比例,因为生产量与时间的比值一定,所以它们之间成正比例。
【点睛】此题考查折线统计图的应用以及辨识成正、反比例的量,主要看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(1)见详解;(2)见详解;(3)见详解;4∶1(4)1∶4=2∶8(答案不唯一)
【分析】(1)数对的表示方法:(列数,行数),根据数对找出A、B、C各点在方格中的对应位置,依次连接各点,并在图中标注各点名称,据此解答。
(2)根据旋转的特征,将三角形绕B点顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)把三角形ABC按2∶1扩大,即三角形的每一条边扩大到原来的2倍,原三角形的底和高分别乘3,得出扩大后三角形的底和高,据此画出扩大后的图形。再根据三角形的面积公式,分别求出原来的三角形和扩大后的三角形的面积,利用比的意义,即可求出放大后三角形的面积与原三角形面积的比。
(4)根据(3)求出的放大后三角形的面积与原三角形面积的比,即可求出比值,根据比例的意义:表示两个比值相等的式子,据此即可写出比例。
【详解】(1)(2)(3)作图如下:
3×2÷2=3(平方厘米)
3×2=6(厘米)
2×2=4(厘米)
6×4÷2=12(平方厘米)
放大后三角形的面积∶原三角形面积的比=12∶3=4∶1。
(4)因为原三角形面积∶放大后三角形的面积=1∶4,
可得1∶4=,,所以可写比例:1∶4=2∶8(答案不唯一)
【点睛】此题主要考查根据数对找位置、图形的旋转、图形的放大与缩小以及比和比例的意义。
13.(1)1∶300000;
(2)174千米。
【分析】(1)根据比例尺的定义,比例尺是图上距离与实际距离的比,把图上距离与实际距离的单元统一一下代入公式即可得解;
(2)根据(1)中得出的比例尺,利用比例的性质即可得解。
【详解】(1)180千米=18000000厘米
60∶18000000=1∶300000
答:这幅宣传图的比例尺是1∶300000。
(2)图上1厘米表示300000厘米,即1厘米表示3千米,
3×58=174(千米)
答:京张高铁实际全线长174千米。
14.(1)1∶50000;
(2)2000米;
(3)见详解
【分析】(1)通过直尺测量,宁宁家到书店的图上距离是2厘米,宁宁家距书店1000米,统一单位后,根据比例尺的意义,比例尺=图上距离∶实际距离,代入数据求出这幅图的比例尺。
(2)经测量,宁宁家到学校的图上距离是4厘米,根据实际距离=图上距离÷比例尺,代入数据即可求出宁宁家到学校的实际距离是多少米。
(3)统一单位后,用实际距离×比例尺=图上距离,求出体育馆和宁宁家两地之间的图上距离,再以宁宁家为观测点,利用地图上的方向“上北下南,左西右东”,根据方向、角度、距离确定体育馆的位置,并在图上标注出来。
【详解】(1)1000米=100000厘米
2∶100000=1∶50000
答:这幅图的比例尺是1∶50000。
(2)4÷
=4×50000
=200000(厘米)
200000厘米=2000米
答:宁宁家到学校的实际距离是2000米。
(3)1500米=150000厘米
150000×=3(厘米)
如图:
【点睛】此题主要考查比例尺的意义以及根据方向、角度、距离确定物体的位置。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
