数学:2.3《函数的应用(ⅰ)》课件(新人教b版必修1)
文档属性
| 名称 | 数学:2.3《函数的应用(ⅰ)》课件(新人教b版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 37.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:13:00 | ||
图片预览


文档简介
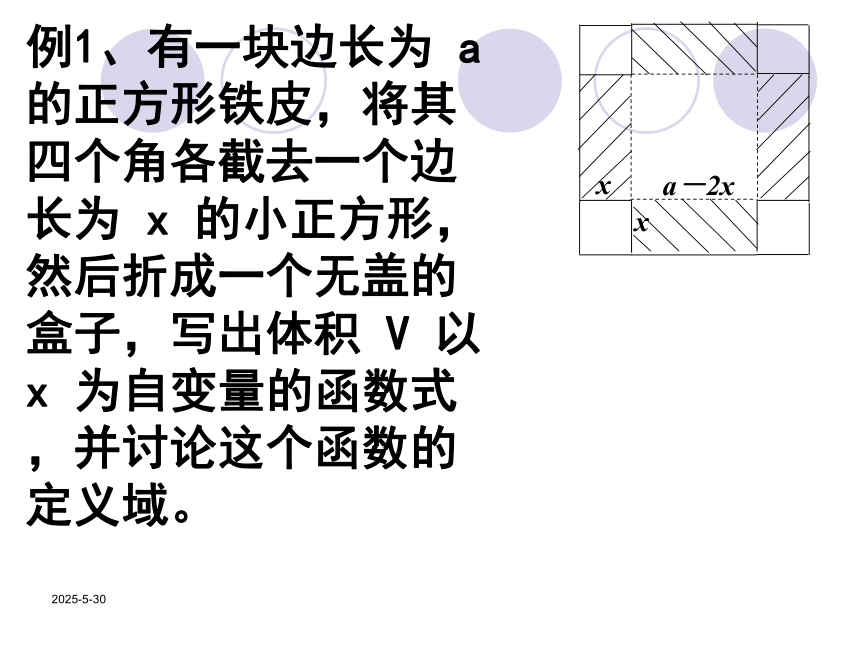
课件6张PPT。2019/3/132.3 函数的应用(1)2019/3/13例1、有一块边长为 a 的正方形铁皮,将其四个角各截去一个边长为 x 的小正方形,然后折成一个无盖的盒子,写出体积 V 以 x 为自变量的函数式,并讨论这个函数的定义域。2019/3/13例2、某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲。【为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好。】若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
⑴把y表示成x的函数,并求出其定义域:
⑵试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
2019/3/13 (2)请你设计礼品价值,以使商场获得最大利润. 练习1:一商场批发某种商品的进价为每个80元,零售价为每个100元,为了促进销售,拟采用买一个这种商品赠送一个小礼品的办法,试验表明,礼品价格为1元时,销售量可增加10%,且在一定范围内礼品价格每增加1元销售量就可增加10%.设未赠送礼品时的销售量为 件. (1)写出礼品价值为 元时,所获利润 (元)关于 的函数关系式;2019/3/13练习2、绿缘商店每月按出厂价每瓶3元购进一种
饮料。根据以前的统计数据,若零售价
定为每瓶4元,每月销售400瓶,若每瓶售
价每降低0.05元,则可多销售40瓶。在每
月 的进货量当月销售完的前提下,请你给
该 商店设计一个方案:销售价格定为多少
元和从工厂购进多少瓶时,才可获得最大
利 润?2019/3/13解函数应用题的方法和步骤:1。审题: (1):设出未知 (2):找出量与量的关系 2。建摸:建立函数关系式 3。求解:用数学方法解出未知 4。回归实际:检验所求结果是否符合实际并作答
⑴把y表示成x的函数,并求出其定义域:
⑵试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
2019/3/13 (2)请你设计礼品价值,以使商场获得最大利润. 练习1:一商场批发某种商品的进价为每个80元,零售价为每个100元,为了促进销售,拟采用买一个这种商品赠送一个小礼品的办法,试验表明,礼品价格为1元时,销售量可增加10%,且在一定范围内礼品价格每增加1元销售量就可增加10%.设未赠送礼品时的销售量为 件. (1)写出礼品价值为 元时,所获利润 (元)关于 的函数关系式;2019/3/13练习2、绿缘商店每月按出厂价每瓶3元购进一种
饮料。根据以前的统计数据,若零售价
定为每瓶4元,每月销售400瓶,若每瓶售
价每降低0.05元,则可多销售40瓶。在每
月 的进货量当月销售完的前提下,请你给
该 商店设计一个方案:销售价格定为多少
元和从工厂购进多少瓶时,才可获得最大
利 润?2019/3/13解函数应用题的方法和步骤:1。审题: (1):设出未知 (2):找出量与量的关系 2。建摸:建立函数关系式 3。求解:用数学方法解出未知 4。回归实际:检验所求结果是否符合实际并作答
