数学:3.2.2《复数的乘法》课件(新人教b版选修2-2)
文档属性
| 名称 | 数学:3.2.2《复数的乘法》课件(新人教b版选修2-2) |

|
|
| 格式 | rar | ||
| 文件大小 | 49.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览



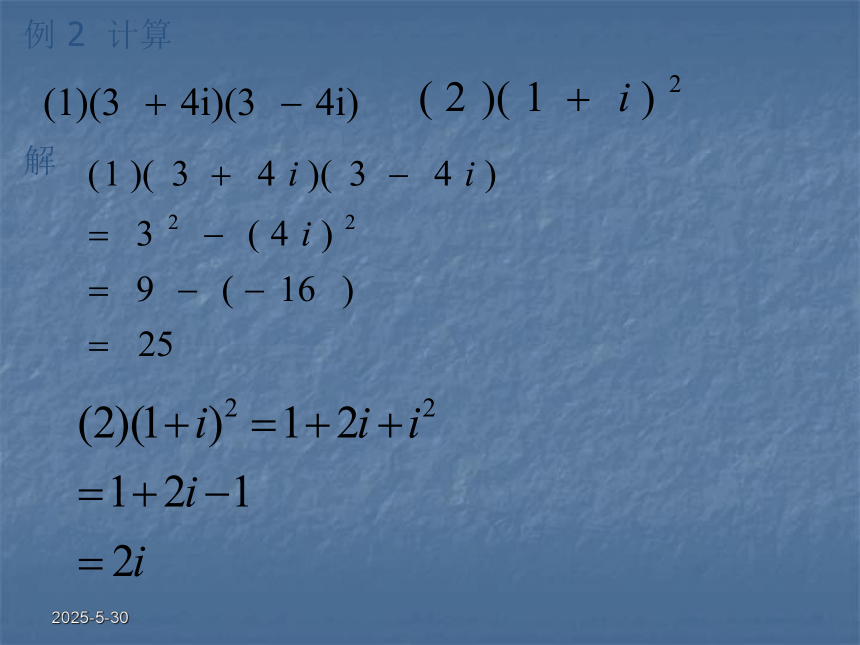



文档简介
课件16张PPT。2019/3/13 复数的乘法2019/3/13一 、复数的乘法法则:(a+bi)(c+di)=ac+bci+adi+bdi2
=(ac-bd)+(bc+ad)i显然任意两个复数的积仍是一个复数. 对于任意z1,z2,z3 ∈ C,有z1?z2= z2?z1 ,
z1?z2 ?z3= z1?(z2 ?z3) ,
z1?(z2 +z3)= z1?z2 +z1?z3 .2019/3/13例 1 计算 (1-2i)(3+4i)(-2+i)解:(1-2i)(3+4i)(-2+i)对于任意复数z=a+bi ,有(a+bi)(a-bi)=a2+b2=(11-2i)(-2+i)=-20+15i .2019/3/13例 2 计算解2019/3/13共轭复数:一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不为0的共轭复数也叫共轭虚数.思考:若 是共轭复数,那么
在复平面内,它们所对应的点有怎样的位置关系?
是一个怎样的数?2019/3/13关于共轭复数的运算性质z1 , z2 ∈C , 则2019/3/13在乘除法运算中关于复数模的性质已知 z1 , z2 ∈C , 求证:| z1 ? z2 |=| z1 | ? | z2 | ,2019/3/13设z1=a+bi , z2=c+di (a,b,c,d ∈R) ,则| z1?z2 |=|(ac-bd)+(bc+ad)i|= | z1 | ? | z2 | 证明:2019/3/13i的乘方规律从而对任意 , 2019/3/13两个特殊复数的乘方1. 计算 2019/3/132. 设计算:2019/3/132019/3/13小结:2019/3/13例7 求复数 ,使 为实数,且 . 解:设2019/3/13①②2019/3/13将 代入②得得将 b=0代入②得 a=4 或 a=0 ∴ Z=4 或 Z=0 (舍)
=(ac-bd)+(bc+ad)i显然任意两个复数的积仍是一个复数. 对于任意z1,z2,z3 ∈ C,有z1?z2= z2?z1 ,
z1?z2 ?z3= z1?(z2 ?z3) ,
z1?(z2 +z3)= z1?z2 +z1?z3 .2019/3/13例 1 计算 (1-2i)(3+4i)(-2+i)解:(1-2i)(3+4i)(-2+i)对于任意复数z=a+bi ,有(a+bi)(a-bi)=a2+b2=(11-2i)(-2+i)=-20+15i .2019/3/13例 2 计算解2019/3/13共轭复数:一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不为0的共轭复数也叫共轭虚数.思考:若 是共轭复数,那么
在复平面内,它们所对应的点有怎样的位置关系?
是一个怎样的数?2019/3/13关于共轭复数的运算性质z1 , z2 ∈C , 则2019/3/13在乘除法运算中关于复数模的性质已知 z1 , z2 ∈C , 求证:| z1 ? z2 |=| z1 | ? | z2 | ,2019/3/13设z1=a+bi , z2=c+di (a,b,c,d ∈R) ,则| z1?z2 |=|(ac-bd)+(bc+ad)i|= | z1 | ? | z2 | 证明:2019/3/13i的乘方规律从而对任意 , 2019/3/13两个特殊复数的乘方1. 计算 2019/3/132. 设计算:2019/3/132019/3/13小结:2019/3/13例7 求复数 ,使 为实数,且 . 解:设2019/3/13①②2019/3/13将 代入②得得将 b=0代入②得 a=4 或 a=0 ∴ Z=4 或 Z=0 (舍)
