数学:3.3.2《线性规划》课件(新人教版a必修5)
文档属性
| 名称 | 数学:3.3.2《线性规划》课件(新人教版a必修5) |  | |
| 格式 | rar | ||
| 文件大小 | 37.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:15:00 | ||
图片预览




文档简介
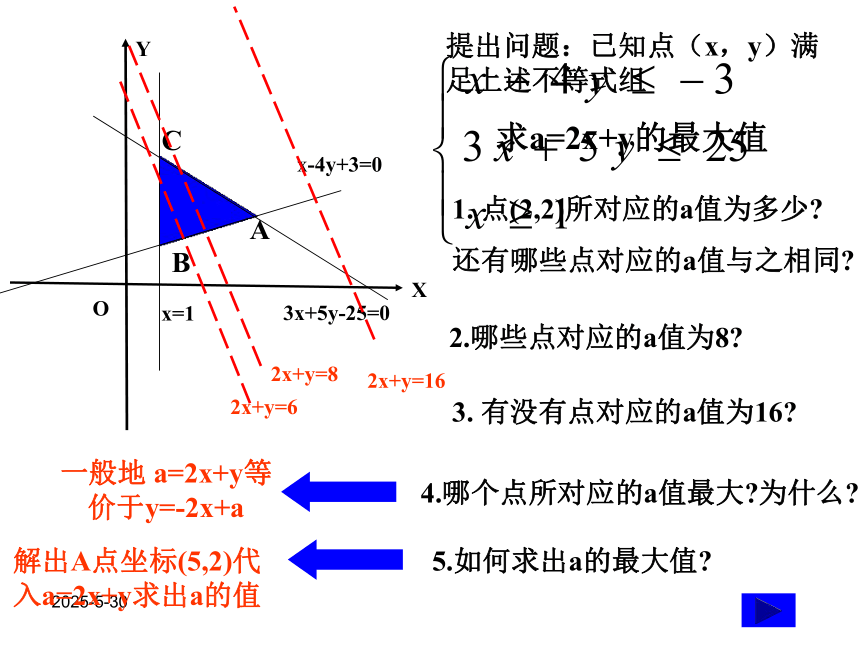
课件12张PPT。2019/3/13简单线性规划2019/3/13美国数学家,美国全国科学院院士。线性规划的奠基人。 1974年丹齐克在总结前人工作的基础上创立了线性规划,确定了这一学科的范围,并提出了解决线性规划问题的单纯形法 1937~1939年任美国劳工统计局统计员,1941~1952年任美国空军司令部数学顾问、战斗分析部和统计管理部主任丹齐克是美国运筹学会和国际运筹学会联合会 (IFORS)的主席和美国数学规划学会的创始人。他发表过100多篇关于数学规划及其应用方面的论文,1963年出版专著《线性规划及其范围》,这本著作至今仍是线性规划方面的标准参考书。 2019/3/13作出不等式组表示的平面区域2019/3/13提出问题:已知点(x,y)满足上述不等式组
求a=2x+y的最大值1. 点(2,2)所对应的a值为多少?
还有哪些点对应的a值与之相同?
2.哪些点对应的a值为8?3. 有没有点对应的a值为16?4.哪个点所对应的a值最大?为什么?5.如何求出a的最大值?2019/3/13有关概念
线性约束条件 : 关于x,y 的一次不等式组成的不等式组
线性目标函数 : 求最大值或最小值所涉及的变量x,y 的
一次解析式
可行解 : 满足线性约束条件的解(x,y)
可行域 : 所有可行解组成的集合
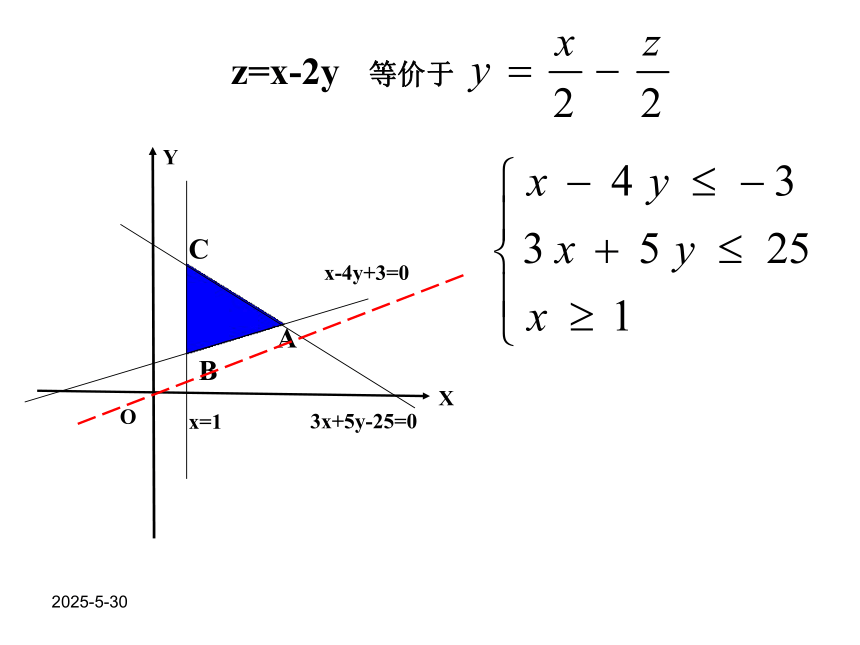
最优解 :使目标函数取得最大值或最小值的可行解2019/3/13 z=x-2y 等价于 2019/3/13解线性规划问题的步骤: (1)画出线性约束条件所表示的可行域;(2)(4)解方程组求出最优解,并代入目 标函数 ,
给出答案。2019/3/13练习巩固
2019/3/13若目标函数z=ax+y仅在点(5,2)处取得最大值,求a的取值范围?2019/3/13思考题:已知x,y满足条件:z=2x-y,且变量x,y为整数,求z的最大值和最小值2019/3/13结论:1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数或与截距有关的量。2019/3/13求解线性规划问题的基本方法是单纯形法,现在已有单纯形法的标准软件,可在电子计算机上求解约束条件和决策变量数达 10000个以上的线性规划问题。为了提高解题速度,又有改进单纯形法、对偶单纯形法、原始对偶方法、分解算法和各种多项式时间算法。对于只有两个变量的简单的线性规划问题,也可采用图解法求解。这种方法仅适用于只有两个变量的线性规划问题。它的特点是直观而易于理解,通过图解法求解可以理解线性规划的一些基本概念。
求a=2x+y的最大值1. 点(2,2)所对应的a值为多少?
还有哪些点对应的a值与之相同?
2.哪些点对应的a值为8?3. 有没有点对应的a值为16?4.哪个点所对应的a值最大?为什么?5.如何求出a的最大值?2019/3/13有关概念
线性约束条件 : 关于x,y 的一次不等式组成的不等式组
线性目标函数 : 求最大值或最小值所涉及的变量x,y 的
一次解析式
可行解 : 满足线性约束条件的解(x,y)
可行域 : 所有可行解组成的集合
最优解 :使目标函数取得最大值或最小值的可行解2019/3/13 z=x-2y 等价于 2019/3/13解线性规划问题的步骤: (1)画出线性约束条件所表示的可行域;(2)(4)解方程组求出最优解,并代入目 标函数 ,
给出答案。2019/3/13练习巩固
2019/3/13若目标函数z=ax+y仅在点(5,2)处取得最大值,求a的取值范围?2019/3/13思考题:已知x,y满足条件:z=2x-y,且变量x,y为整数,求z的最大值和最小值2019/3/13结论:1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数或与截距有关的量。2019/3/13求解线性规划问题的基本方法是单纯形法,现在已有单纯形法的标准软件,可在电子计算机上求解约束条件和决策变量数达 10000个以上的线性规划问题。为了提高解题速度,又有改进单纯形法、对偶单纯形法、原始对偶方法、分解算法和各种多项式时间算法。对于只有两个变量的简单的线性规划问题,也可采用图解法求解。这种方法仅适用于只有两个变量的线性规划问题。它的特点是直观而易于理解,通过图解法求解可以理解线性规划的一些基本概念。
